计算过程

1. 采样点生成

在角度区间[0, π]上均匀采样 30 个点：
θ_i = (i-1) × π/29, i = 1,2,...,30

2. 最小二乘拟合

设拟合多项式为：y = a₀ + a₁x + a₂x² + a₃x³ + a₄x⁴ + a₅x⁵

最小二乘法的正规方程：
AᵀA × [a₀,a₁,a₂,a₃,a₄,a₅]ᵀ = AᵀY
其中 A 是范德蒙德矩阵：

A = [1, x, x², x³, x⁴, x⁵]

3. 拟合误差计算

均方误差：MSE = (1/n) × Σ(y_i - ŷ_i)²
其中ŷ_i 是拟合值

Python 程序实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 在单位半圆上均匀采样30个点
n_points = 30
theta = np.linspace(0, np.pi, n_points)  # 在[0, π]上均匀采样角度
x = np.cos(theta)  # x坐标
y = np.sin(theta)  # y坐标

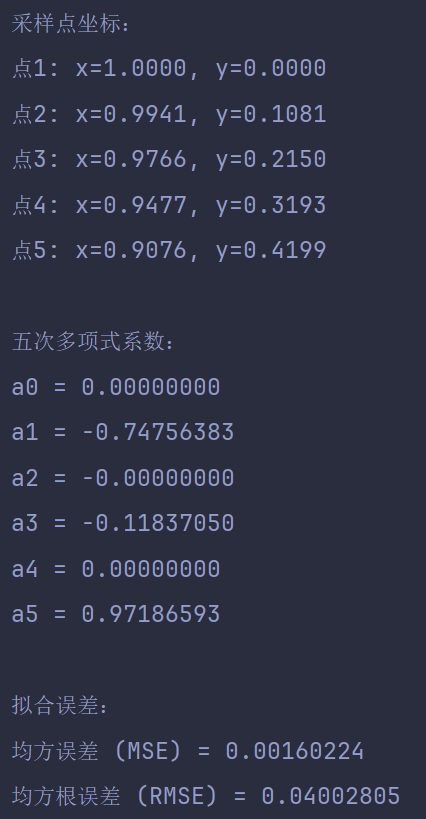
print("采样点坐标：")
for i in range(min(5, n_points)):
    print(f"点{i+1}: x={x[i]:.4f}, y={y[i]:.4f}")

# 2. 构建最小二乘拟合的五次多项式
degree = 5

# 构建范德蒙德矩阵
A = np.vander(x, degree + 1)

# 使用最小二乘法求解系数
coefficients, residuals, rank, s = np.linalg.lstsq(A, y, rcond=None)

print(f"\n五次多项式系数：")
for i, coef in enumerate(coefficients):
    print(f"a{i} = {coef:.8f}")

# 3. 计算拟合值
y_fit = np.polyval(coefficients, x)

# 4. 计算拟合误差
mse = mean_squared_error(y, y_fit)
rmse = np.sqrt(mse)

print(f"\n拟合误差：")
print(f"均方误差 (MSE) = {mse:.8f}")
print(f"均方根误差 (RMSE) = {rmse:.8f}")

# 5. 可视化结果
plt.figure(figsize=(12, 8))

# 绘制原始半圆和采样点
theta_continuous = np.linspace(0, np.pi, 100)
x_circle = np.cos(theta_continuous)
y_circle = np.sin(theta_continuous)

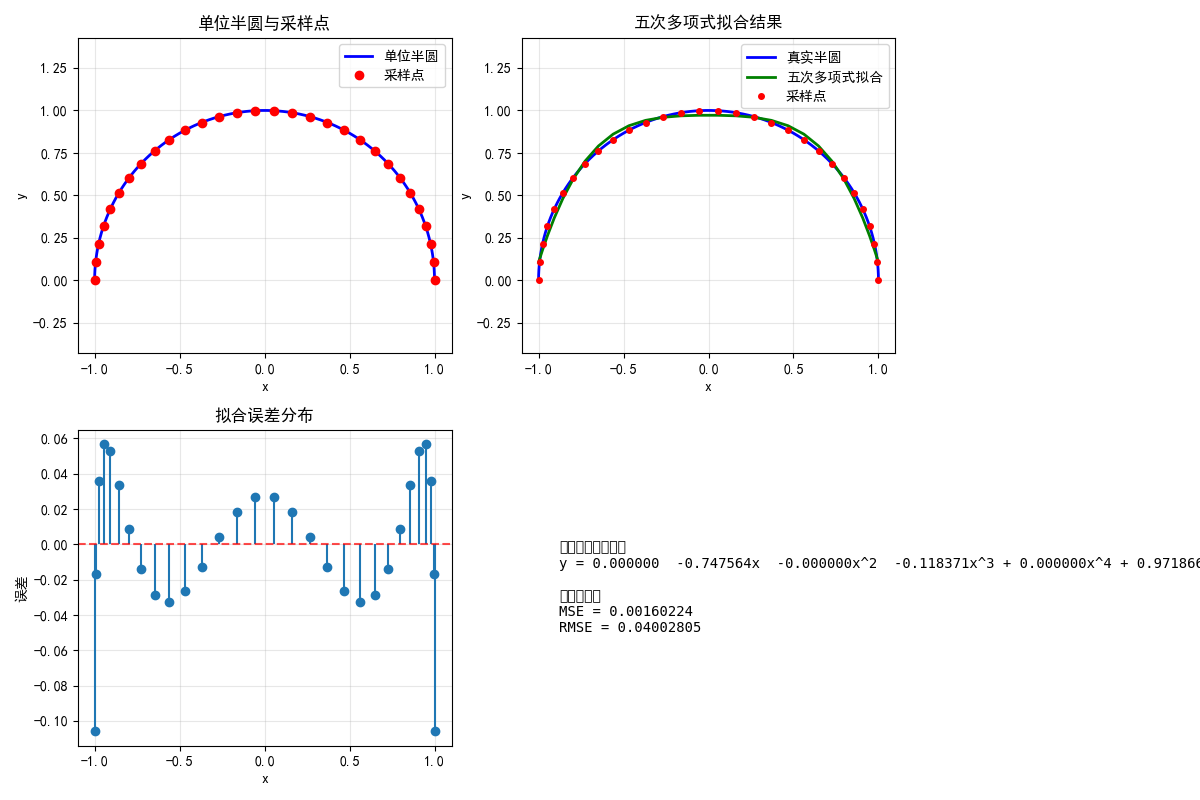
plt.subplot(2, 2, 1)
plt.plot(x_circle, y_circle, 'b-', label='单位半圆', linewidth=2)
plt.plot(x, y, 'ro', markersize=6, label='采样点')
plt.xlabel('x')
plt.ylabel('y')
plt.title('单位半圆与采样点')
plt.axis('equal')
plt.legend()
plt.grid(True, alpha=0.3)

# 绘制拟合结果
plt.subplot(2, 2, 2)
plt.plot(x_circle, y_circle, 'b-', label='真实半圆', linewidth=2)
plt.plot(x, y_fit, 'g-', label='五次多项式拟合', linewidth=2)
plt.plot(x, y, 'ro', markersize=4, label='采样点')
plt.xlabel('x')
plt.ylabel('y')
plt.title('五次多项式拟合结果')
plt.axis('equal')
plt.legend()
plt.grid(True, alpha=0.3)

# 绘制误差分布
plt.subplot(2, 2, 3)
errors = y - y_fit
plt.stem(x, errors, basefmt=" ")
plt.axhline(y=0, color='r', linestyle='--', alpha=0.7)
plt.xlabel('x')
plt.ylabel('误差')
plt.title('拟合误差分布')
plt.grid(True, alpha=0.3)

# 多项式表达式
plt.subplot(2, 2, 4)
plt.axis('off')
poly_text = "五次拟合多项式：\n"
poly_text += f"y = {coefficients[0]:.6f}"
for i in range(1, degree + 1):
    sign = '+' if coefficients[i] >= 0 else ''
    poly_text += f" {sign} {coefficients[i]:.6f}x"
    if i > 1:
        poly_text += f"^{i}"
error_text = f"\n\n拟合误差：\nMSE = {mse:.8f}\nRMSE = {rmse:.8f}"
plt.text(0.1, 0.5, poly_text + error_text, fontsize=10, 
         verticalalignment='center', fontfamily='monospace')

plt.tight_layout()
plt.show()

# 输出详细结果
print("\n详细计算结果：")
print("=" * 60)
for i in range(n_points):
    print(f"点{i+1:2d}: x={x[i]:8.4f}, y_true={y[i]:8.4f}, y_fit={y_fit[i]:8.4f}, 误差={errors[i]:8.4f}")
print("=" * 60)

程序运行结果