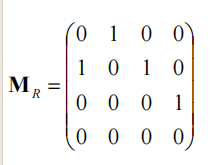题型

填空

证明

图论：9和12的概念

• 9 握手定理、连通、特殊的图（完全图正则图）
• 12 加一边有圈，去一边不连通；
• 13
• 14？
  集合论
  集合相等

解答

• 10
• 11 每个矩阵怎么求、三个矩阵的关系（从一个求另一个）
• 12 huffman编码 最优二元树
• 13
• 14 最大匹配、从X到Y的匹配（从X到Y的匹配一定是最大匹配）
• 图的建模（混合 欧拉图哈密顿图二分图树）

集合

证明：集合A=B

• 法1：使用集合相等的定义，证明：对于任意 ，
• 法2：证明 且 ，即 ，，，
• 法3：利用已知集合恒等式进行等式推演
• 法4：特征函数相同

证明：判断偏序

偏序：自反，反对称，传递
严格偏序：反自反，（反对称），传递
全序：偏序+任意两个元素可比
良序：偏序+任意非空子集有最小元

求：画哈斯图

省略自环、有向边的方向、某些定点之间的边

求：八大关系

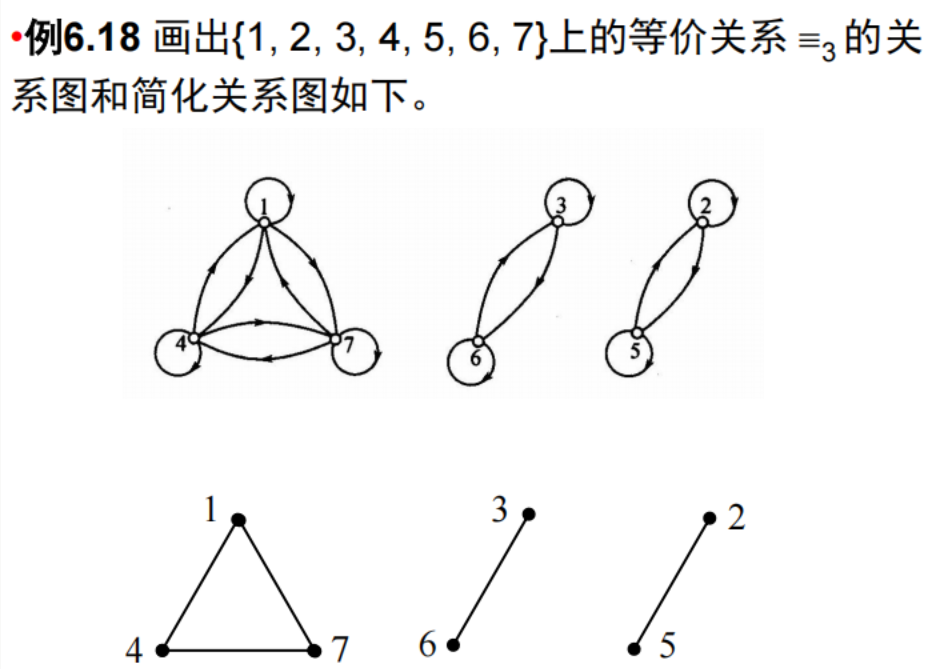
证明：等价关系

自反，对称，传递

求：画简图

不画箭头、双向二合一为无向

求：等价关系与划分的转化

求：集合表达式、关系矩阵、关系图、满足哪些关系

自反、反自反、对称、反对称、传递

树、图

概念！！！！

• 桥、生成树

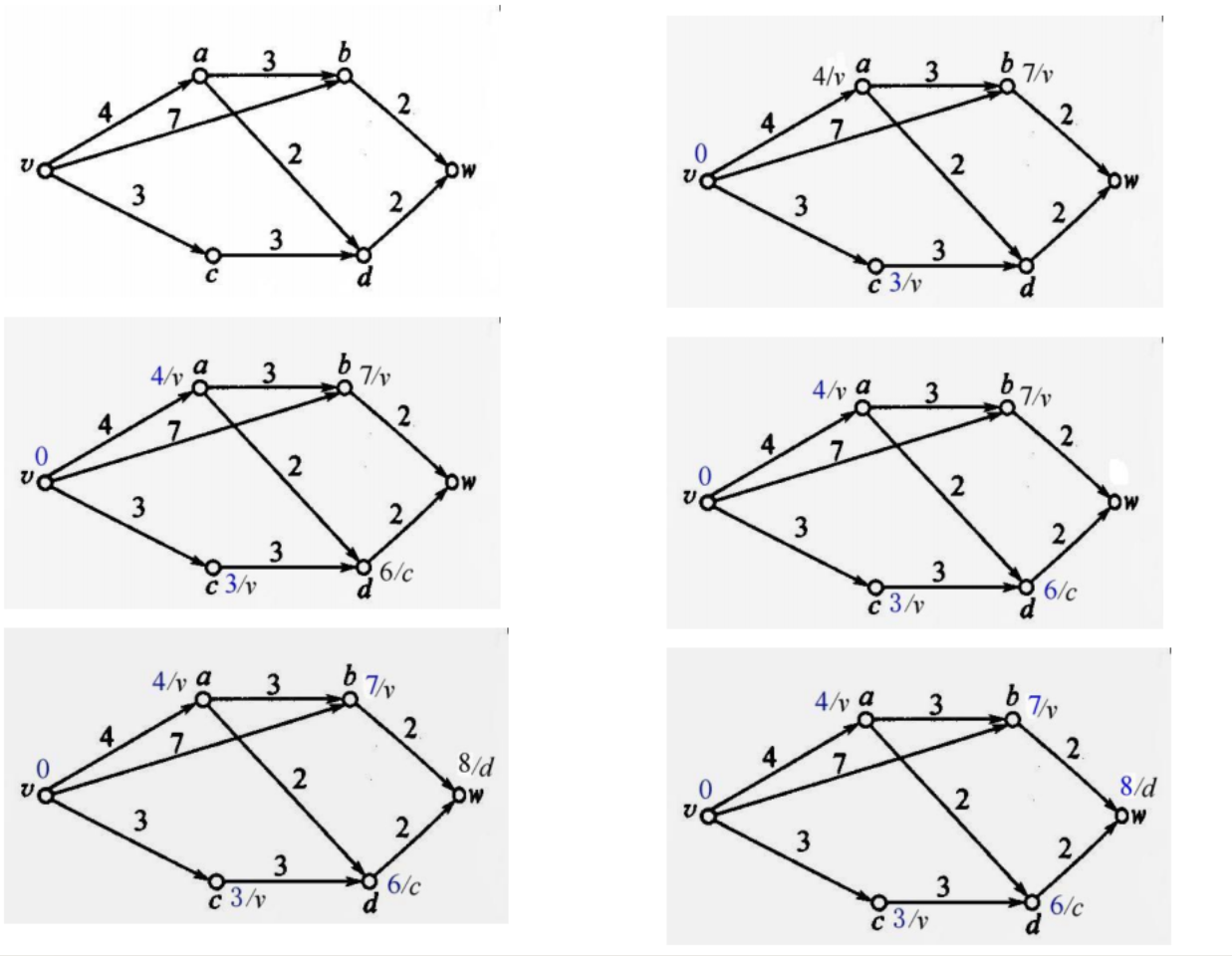
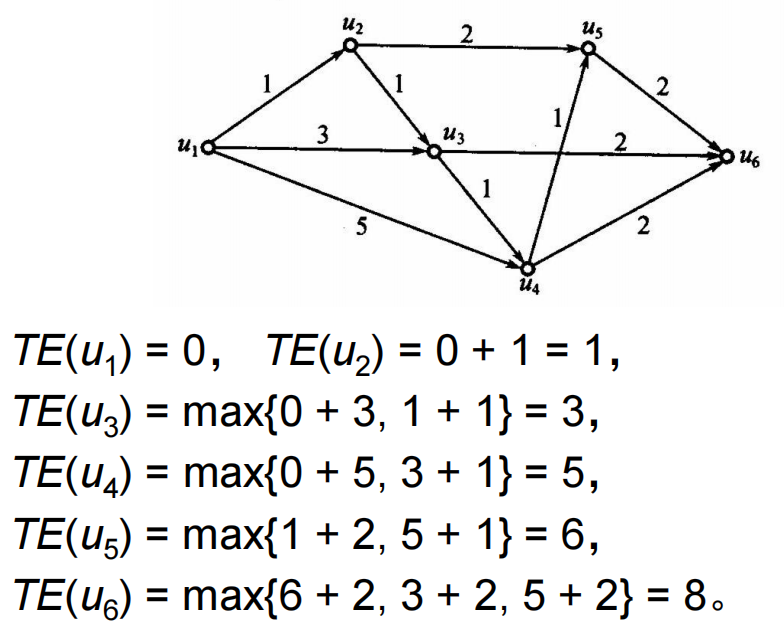
求：最短路

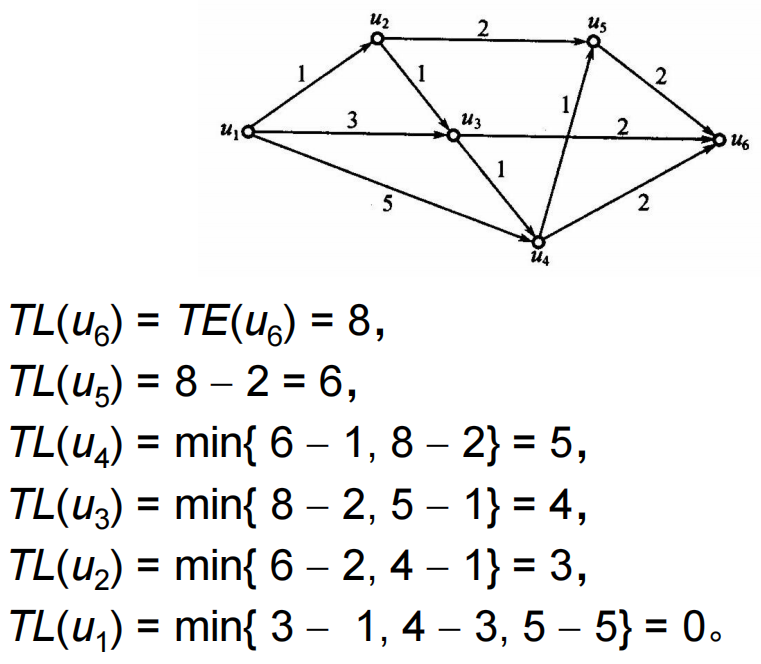
求：关键通路

• 关键通路：在工序流线图中，从发点到收点的最长通路称为关键通路。**事件 在某条关键通路上当且仅当它的最早完成时间和最迟完成时间相等。
• 最早完成时间：在工序流线图中，从发点 到事件 的最长通路的长度称为事件 的最早完成时间，记为 。
  
• 最迟完成时间：给定工序流线图，在保证收点 的最早完成时间不增加的前提下，自发点 最迟到达事件 的时间称为 的最迟完成时间，记为 。
  
• 缓冲时间：给定工序流线图 ，，定义 的缓冲时间 。
  • 事件 的发生可以比预定的最早完成时间推迟缓冲时间 ，而不会影响整个工程的进度。
  • 关键通路上的所有事件的缓冲时间都是0，即它们都要准时发生，不能推迟，并且关键通路上的工序都要按时完成，不能推迟。

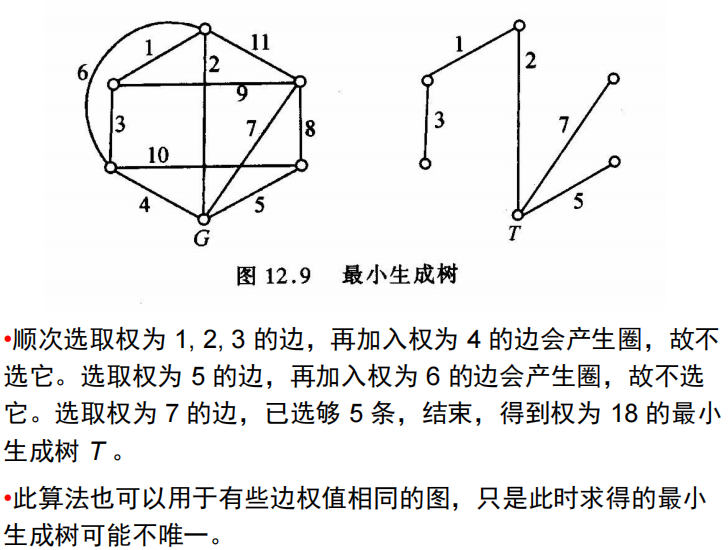
求：最小生成树

求：最优二元树

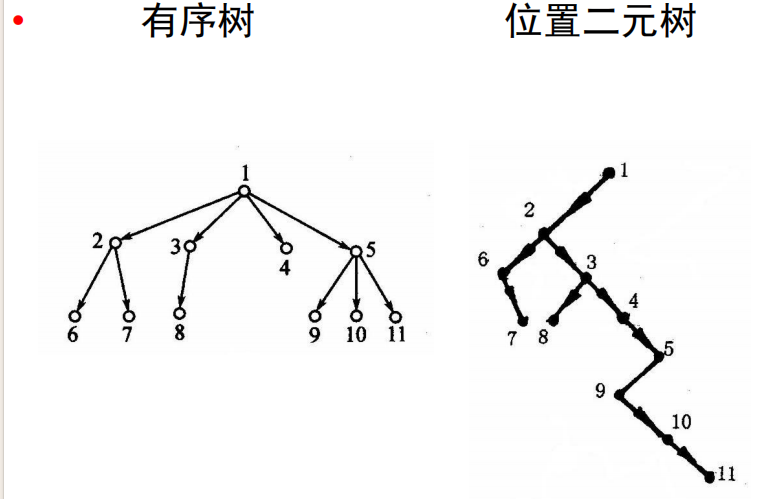
求：有序树转换为位置二元树

• 若 u 是原来有序树的树根，则它仍然是转换后的位置二元树的树根。
• 在原来有序树中，
  • 若顶点 u 是 v 的大儿子，则在转换后的位置二元树中，u 是 v 的左儿子；
  • 若顶点 u 是 v 的大兄弟，则在转换后的位置二元树中，u 是 v 的右儿子。
    

判断：是否是欧拉图

• 连通无向图 是欧拉图当且仅当 的每个顶点都是偶顶点。
• 强连通有向图 是欧拉图当且仅当 中每个顶点的引入次数与引出次数相同。

判断：是否是欧拉链

• 在连通无向图 中存在连接顶点 和 的欧拉链当且仅当只有 和 是奇顶点。
• 单向连通有向图 有从顶点 到 的欧拉通路当且仅当 的引出次数比引入次数大1， 的引入次数比引出次数大1， 中其它顶点的引入次数与引出次数相同。

判断：是否是哈密顿图

• 必要条件：若无向图 ＝ 是哈密顿图， 是 的非空真子集，则 。
• 充分条件：设 ，若 阶简单无向图 中每对不相邻顶点次数之和 ，则 是哈密顿图。

判断：是否是哈密顿链

• 必要条件：若无向图 ＝ 有哈密顿链， 是 的非空真子集，则 。其中 是从 中删除 中所有顶点及它们关联的边所得子图的连通分支数。
• 充分条件：若 阶简单无向图 中每对不相邻顶点次数之和 ，则在 中存在哈密顿链。

判断：是否是二分图

非平凡无向图 是二分图当且仅当 的每个圈的长度都是偶数。

证明：是否是二分图

构造两个点的集合，证明二者互补

求：二分图的最大匹配

最大匹配：在二分图 的所有匹配中，边数最多的匹配称为最大匹配。

求：从X到Y的匹配

1. 先任意找 中一个匹配 作为初始匹配.
2. 如果 还不是从 到 的匹配, 即有 为非饱和顶点.
3. 根据相异性条件, 设 有邻接顶点 :
   • 若有某个 为非饱和顶点, 则可扩充 进 ;
   • 若这 个邻接顶点都是饱和顶点,
     1. 则可构造 条以 为起点的交替链,
     2. 并基于相异性条件, 必可找到一条可扩充链.

证明：存在从X到Y的匹配

• 先用t条件（充分条件）：设 和 是二分图 的互补顶点子集。若存在正整数 ，使得 中每个顶点的次数 ，而 中每个顶点的次数 ，则 中存在从 到 的匹配。
  • 成立：存在
  • 不成立，用充要条件：设 和 是二分图 的互补顶点子集。 中存在从 到 的匹配当且仅当满足以下相异性条件：对于 的任意子集 ，。
    • 成立：存在
    • 不成立：不存在

技巧

数学归纳法

• 第一数学归纳法：第一个成立 + 只要k成立，k+1就成立
  
• 第二数学归纳法：比我小的成立，我就成立
  19-20 二.3
  
  

证明充要条件

“a的充要条件是b”，即证明“a当且仅当b”

• 充分性证明：“如果b成立，那么a一定成立”
• 必要性证明：“如果a成立，那么b一定成立”

“a是b的充要条件”，即证明“b当且仅当a”

• 充分性证明：“如果a成立，那么b一定成立”
• 必要性证明：“如果b成立，那么a一定成立”

a当前仅当b

• 充分性证明：“如果b成立，那么a一定成立”
• 必要性证明：“如果a成立，那么b一定成立”