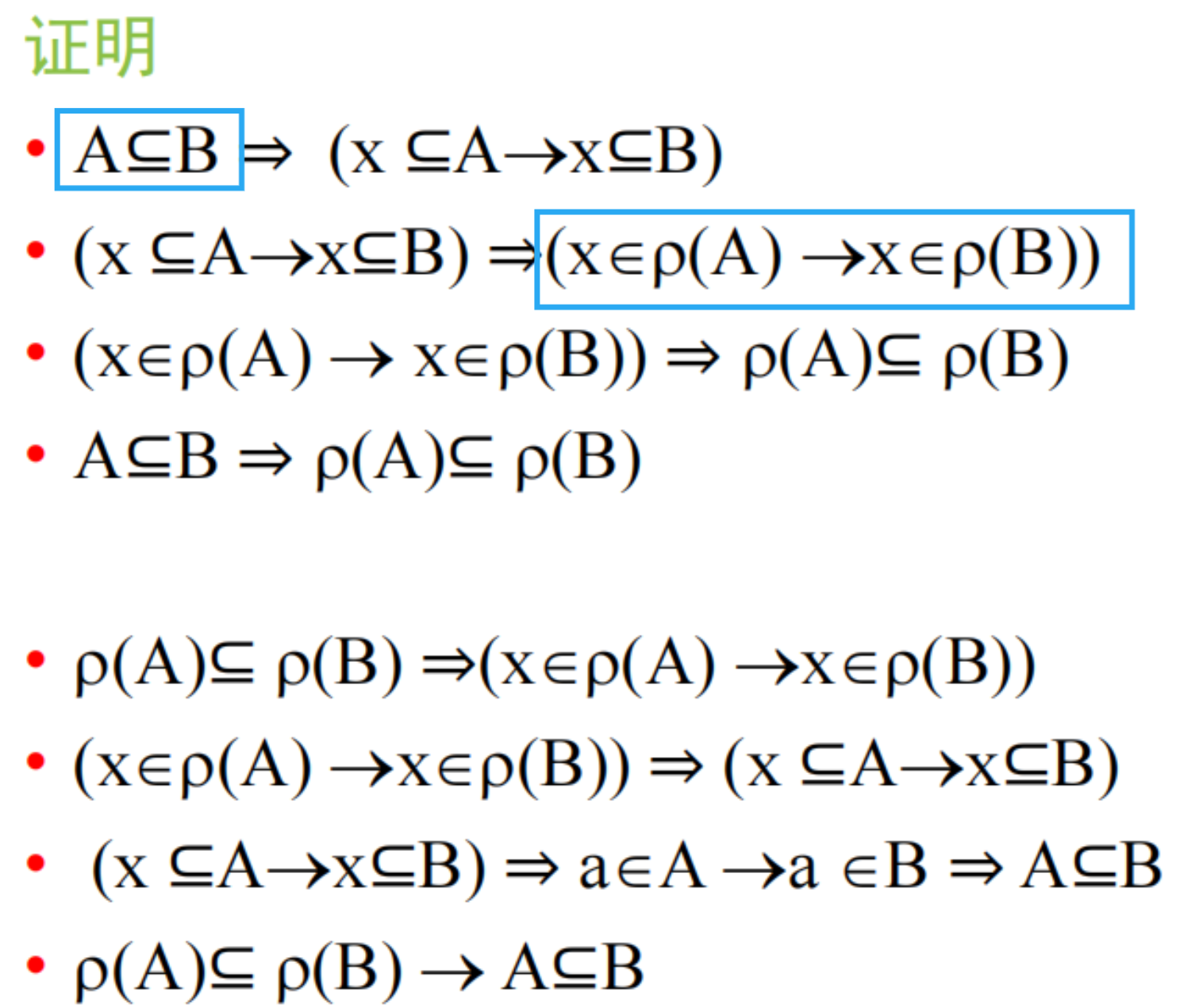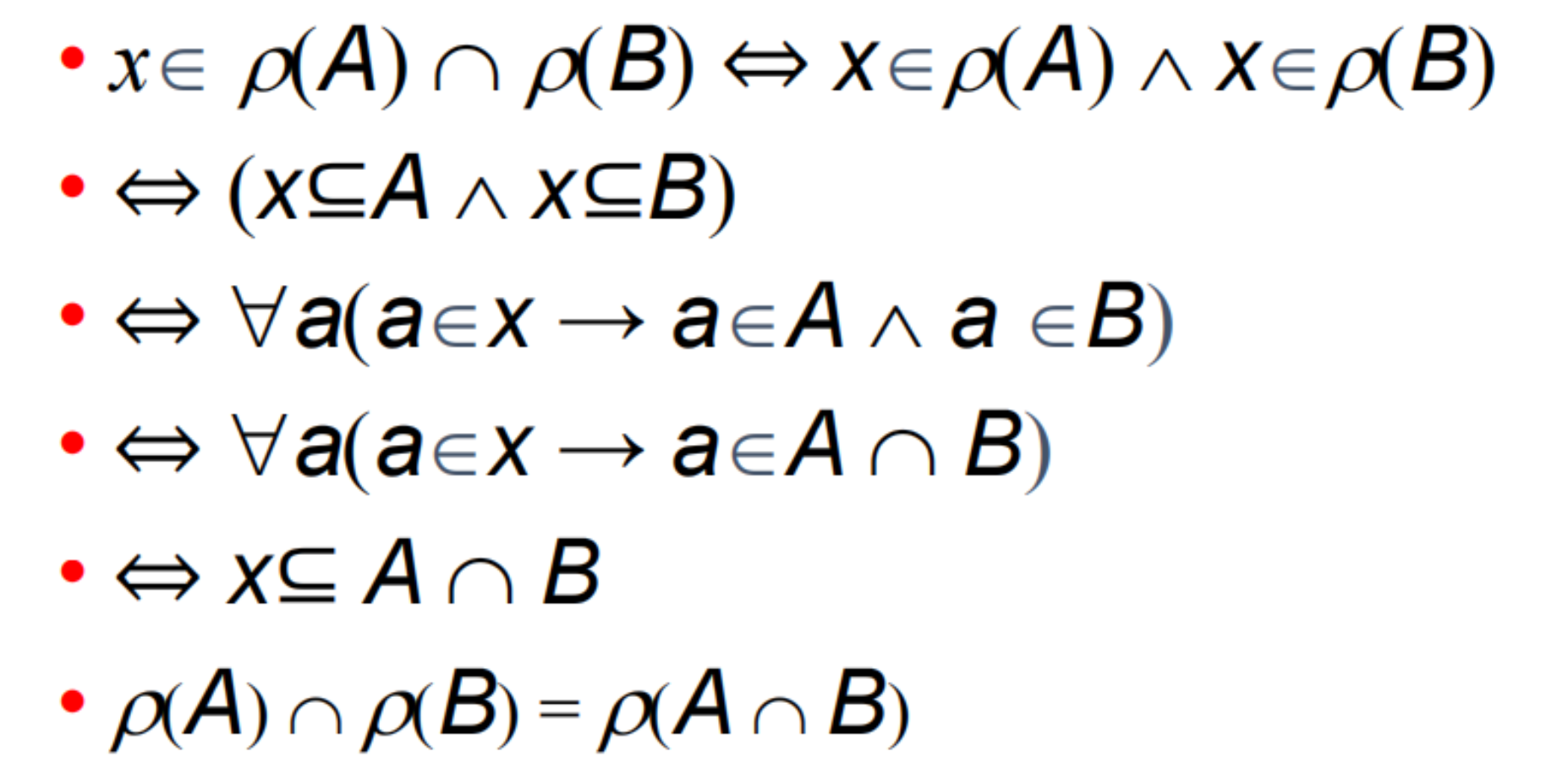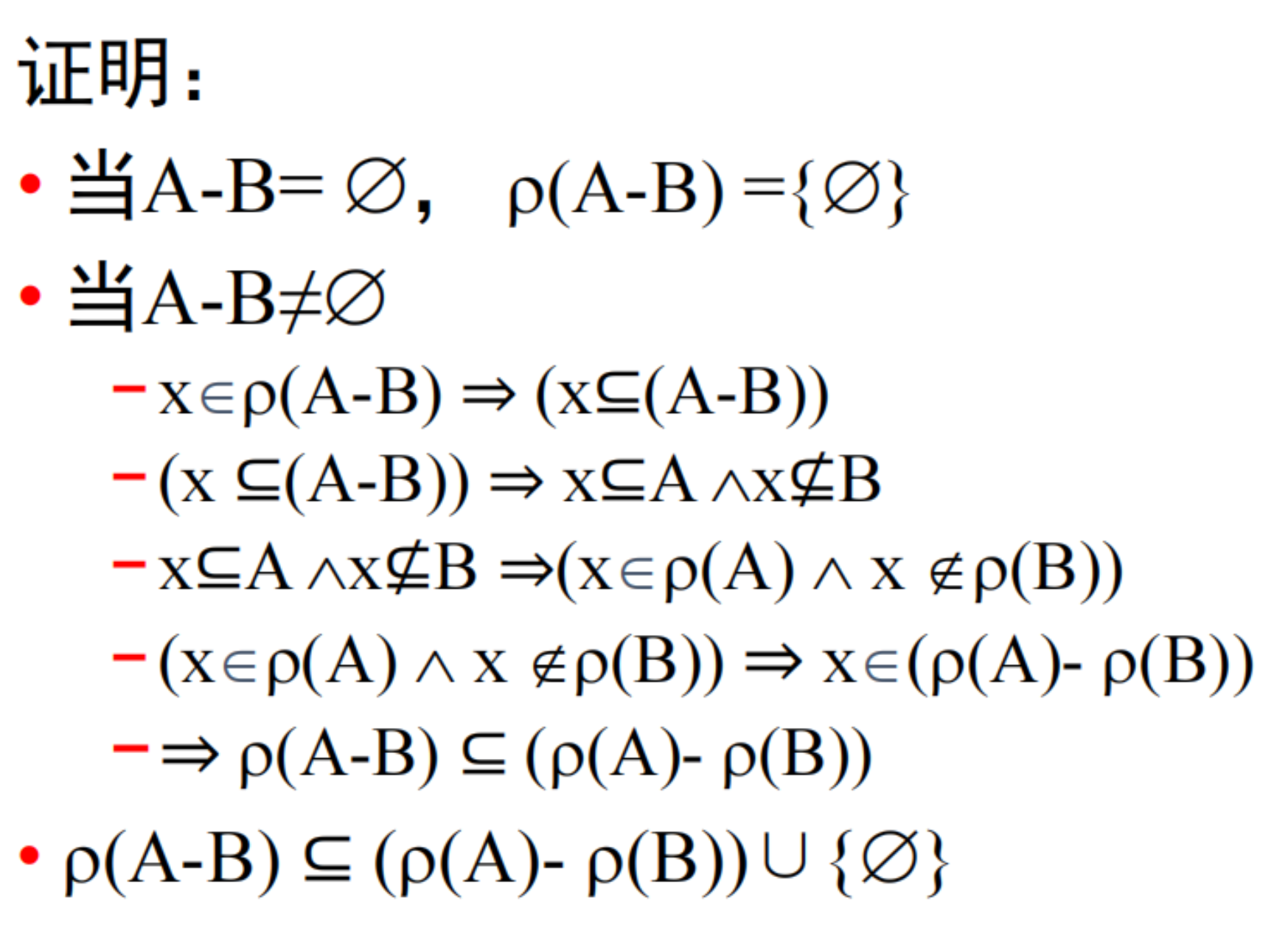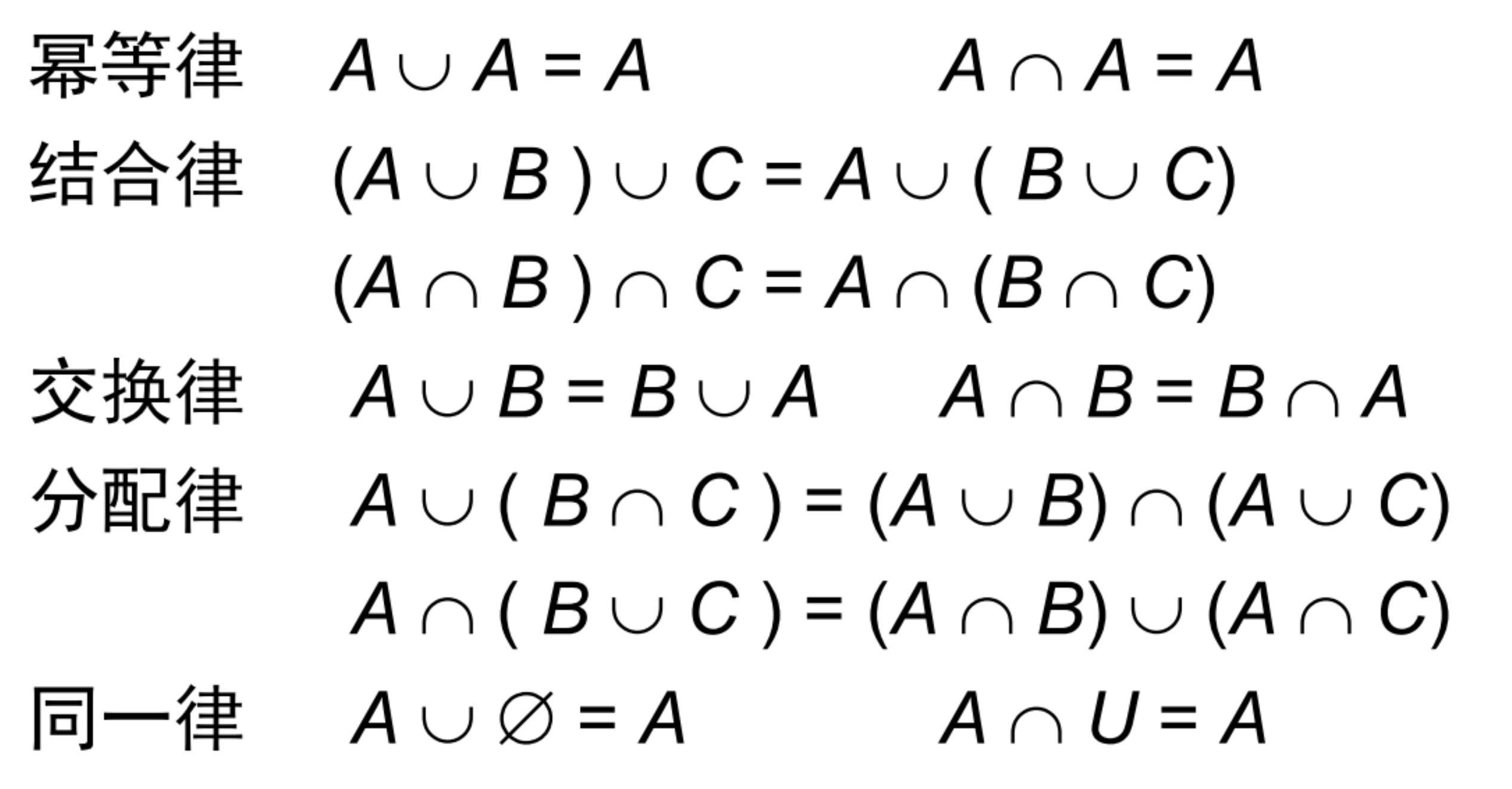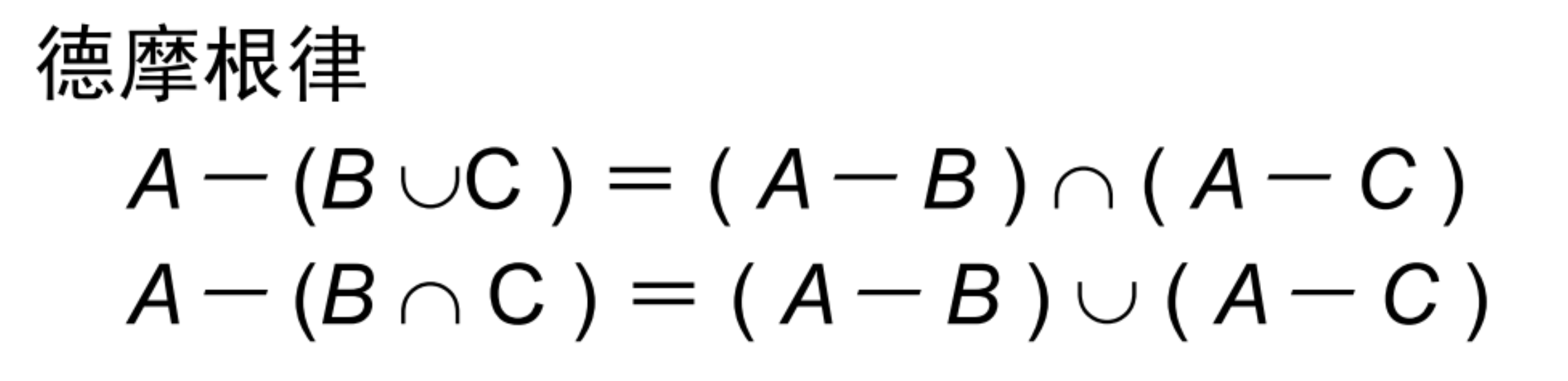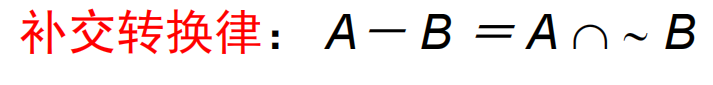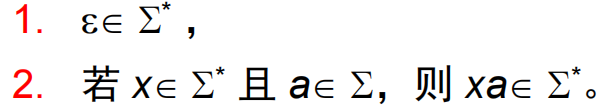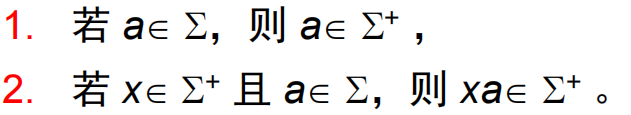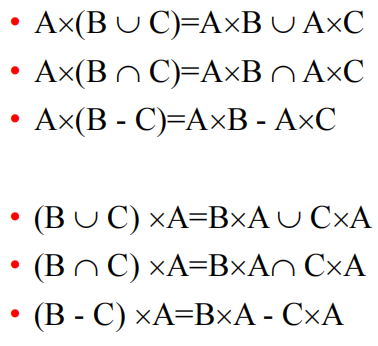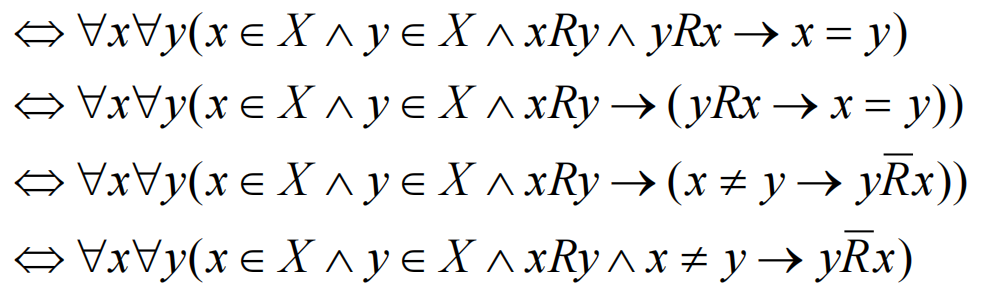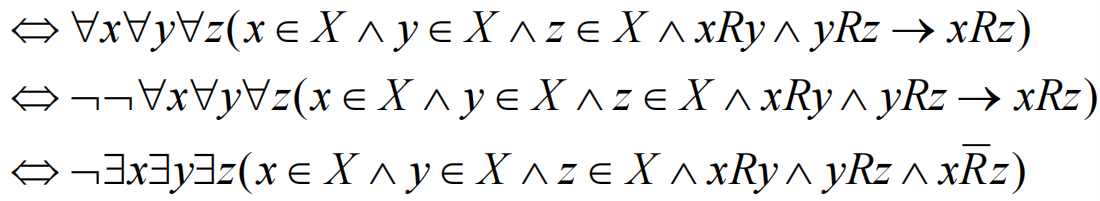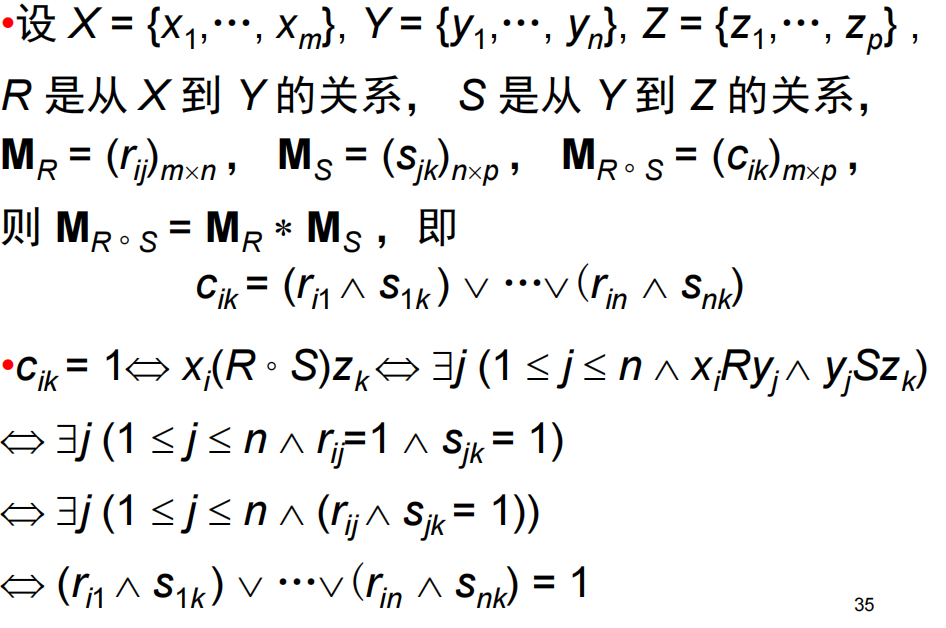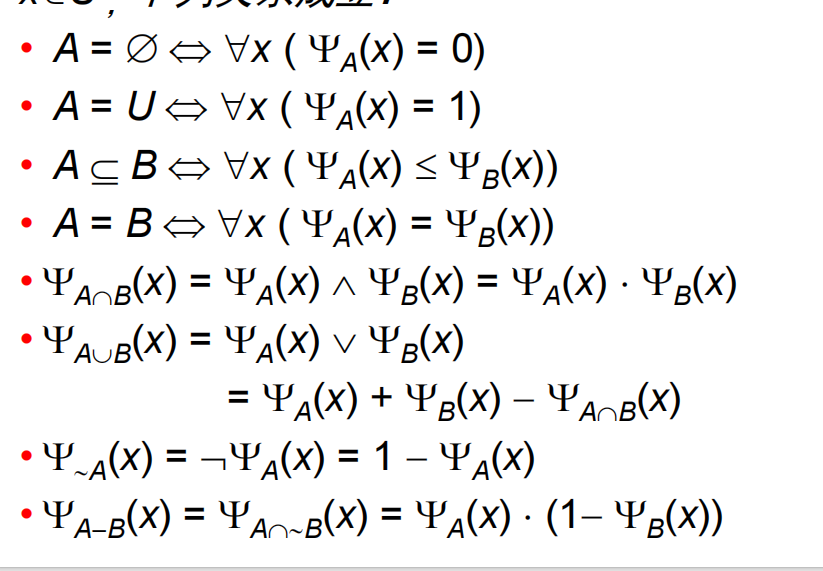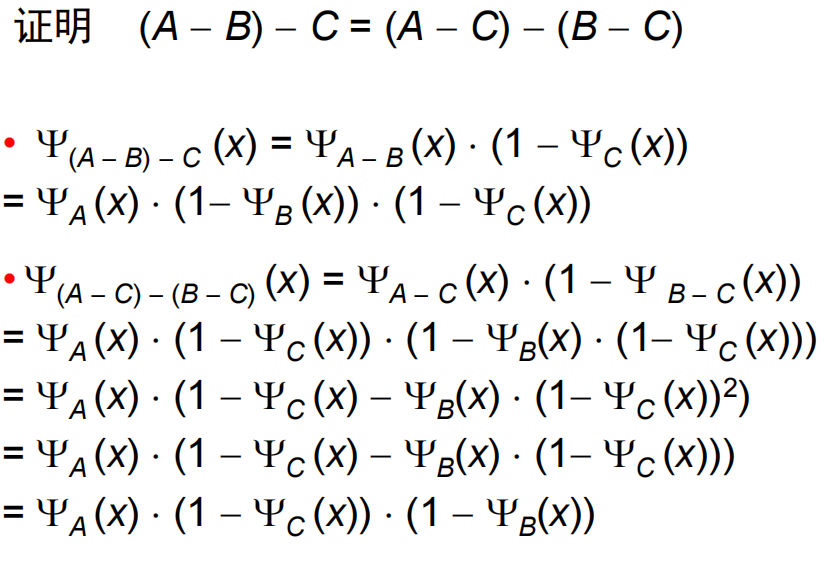第5章 集合的基本概念及其运算

1. 枚举法/抽象法表示集合1.4 2.6
2. 给集合写幂集6.4；幂集的相关证明9 17
3. 集合的运算（加上幂集）10.8；证明恒等式11.7 12.3；给集合写幂集/广义并/广义交15.3 15.4
4. 包含排斥原理19
5. 给集合写集合的乘积21.1 21.3
6. 给集合写笛卡尔乘积24.2；笛卡尔相关证明

5.1 集合与元素

• 常用集合：自然数集 、整数集 、有理数集 、实数集 、复数集 、素数集
• { x | x 是高个子} 不是集合，是一个模糊数学中的模糊集合，因为高个子是一个模糊概念。

5.2 集合间的相等和包含关系

• 外延公理(A=B)：当且仅当 两集合都含有相同的元素时，称 和 相等，记为 。

  特别的，{1, 2, 3} = {2, 1, 3} 集合中元素无次序； {1, 1} = {1} 不考虑集合中元素的出现次数，集合是每个元素的重数都是 0 或 1 的多重集

• 定理5.1： 当且仅当 且 。
• 定理5.2：若 且 ，则 。
• 定理5.4：空集 是唯一的
• 单元集、n元集、有穷集、无穷集

5.3 幂集

• 幂集： 的所有子集组成的集合称为 的幂集，记为 ，即 ，或者 。
  • 空集的幂集仅含有元素 ，即
  • 对于任意集合 ， ，
• 基数和幂集的基数
  • 基数：有穷集 的元素个数称为 的基数，记为 。
  • 定理5.5：
• 幂集的性质
  • 
    
  • 
    
  • 
    
  • 
    

5.4 集合的运算

1 简单计算

• 交集、并集、差集
  • 和 的差集，也称为 关于 的相对补集，
• 聚合/集合族：如果集合 中的每个元素都是集合，则称 为集合的聚合，或者集合族
• 不相交：集合 和 没有公共元素，即 。
• 不相交聚合：设 是一个集合的聚合，如果 中任何两个不同的元素都是不相交的，则称该聚合为不相交聚合，不相交聚合的元素互称为互不相交的元素
• 补集： 的补集 ，对任意的集合 ，若，则
• 对称差集： 和 的对称差集

2 集合恒等式

• 集合恒等式
  
  
  • 集合代数满足对偶定理：在不含 和 的恒等式中，将 和 互换， 和 互换，得到的仍然是恒等式
  • 将不含 和 的命题逻辑等值式中的 换为 ， 换为 ， 换为 ， 换为 ， 换为 ， 换为 ， 换为 ，就得到集合恒等式
    集合恒等式 A=B的证明方法
• 法1：使用集合相等的定义，证明：对于任意 ，
• 法2：证明 且
• 法3：利用已知集合恒等式进行等式推演
• 例
  • 定理5.9：设 是全集 的子集。 当且仅当 和
    
  • 
    
  • 

3 广义并、广义交

• 广义并、广义交

  • 广义并： 的所有元素的并集
    若 ，则 至少是 的某个元素的元素
  • 广义交：若， 的所有元素的交集
    若 ，则 必须是 的每个元素的元素

  有时将集合族的元素表示为带角标的集合，如，称 为角标集。这里角标集 可以是空集，有穷集，也可以是无穷集。
  也将 记为 ，将 记为

5.5 有穷集的计数原理

• 设 和 是两个不相交的有穷集，即 ，则
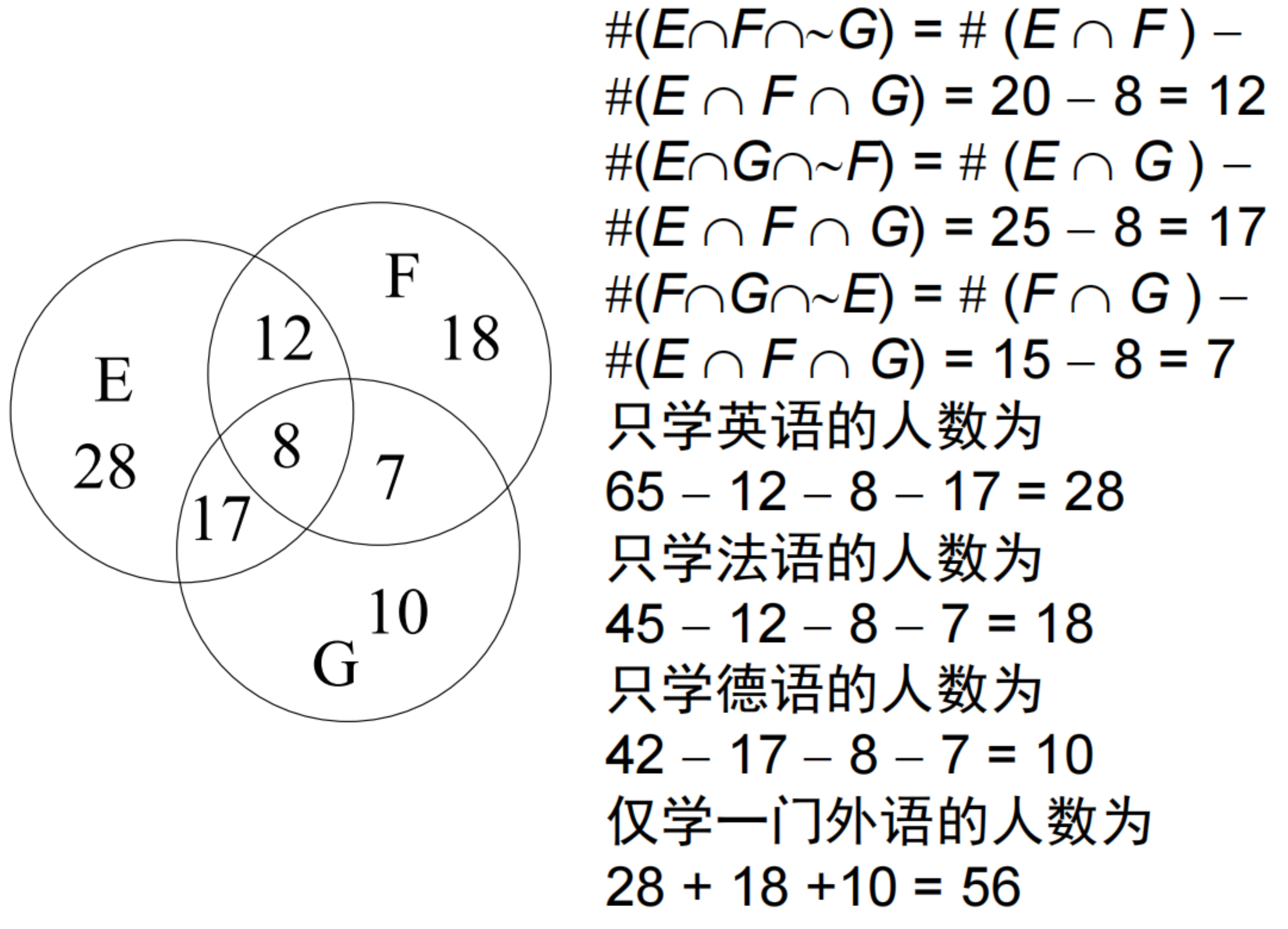
• 包含排斥原理：若 和 是有穷集，则
  • 推论：若 是有穷集，则
    
  • 推广：设 是有限集合，其基数分别为 ，则
    

5.6 集合的归纳定义法

集合归纳定义的三个组成部分

1. 基础语句：直接规定某些对象是该集合的元素。这保证了所定义的集合是非空的,同时也规定了构造集合的原子元素。
2. 归纳语句：规定由已知元素得到新元素的办法。
3. 极限语句：限定集合的范围，规定了哪些对象不是该集合的元素，保证了定义的集合是唯一的
   极限语句常省略不写
   非负偶数集 E 可归纳定义如下：
   基础语句 ,
   归纳语句 若 , 则 。

字母表

• 字母表（符号集）：符号的有穷非空集合，用 表示，称 中元素为符号或字母

• 上的字或串：有限长的字符串，其中每一个字符都是 字母表中的元素。

• 长度：字 中含有的符号个数称为 的长度，记为 。

• 空串：长度为 0 的字称为空串，记为 。显然对任一字母表 ，都是 上的字符串。

• 连接：字母表 上的字 x 和 y 的连接是将 y 接在 x 后面得到的字，记为 xy 。
  连接运算满足结合律；
  连接运算不满足交换律；
  对于任意字x，

• 所有 上字的集合 可归纳定义如下：
  

• 所有 上非空字的集合 可归纳定义如下：
  
  显然，

• 设 ，，则串 定义如下：

  1. ，
  2. 。

• 称 的子集为 上的语言

• 上的语言 A 和 B 的乘积
  
  
  乘积运算满足结合律
  乘积运算不满足交换律

• 定义5.20 设 ，， 定义如下：

  1. ，
  2. 。
     是语言A本身n次乘积的结果。

• 定理5.13
  

• 定理5.14：设 ， m 和 n 是自然数。

  3. 若 ，则 。

• 设A是的子集，则

  • ＝是自然数，即＝＝，集合称为星闭包或简称闭包
  • 集合定义为：＝＝，集合称为A的正闭包

• 定理5.15
  

5.7 有序偶和笛卡儿乘积

• 设 n > 2，n 重序偶定义为
• 集合 A 和 B 的笛卡儿乘积 定义为：。
• 对于任意有穷集合 A 和 B ，
• 笛卡尔积的性质
  

第6章 关系

1. dom、ran相关的证明(2)；关系的性质相关的证明(3)；给图问关系(5)
2. 求复合关系(8)；复合相关的证明(12)；画自反、传递、对称闭包的关系图(13)；闭包相关的证明(14.3 15.3)
3. 画哈斯图、求最大最小元等(18)；判别偏序/线序/全序/良序(20 23)
   是偏序？->哈斯图->八大关系
4. a
   是等价？->画简图->

6.1 关系及其性质

• 二元关系（关系）：有序偶的集合

• 从 到 的关系、 上的关系

• 集合 上的二元关系的数目：如果 ，那么 ， 上的二元关系就有 种

• 全域关系（）、空关系（）、恒等关系（）

• <x,y>：定义域 ；值域

• 关系矩阵 ： 为 到 的关系，若 则关系矩阵i行j列元素 ；否则

• 布尔矩阵的乘法：正常乘，大于等于1就是1，否则是0

• ：设 和 都是 行 列的矩阵，如果 的对应元素都小于等于 的对应元素，则记为 。

• 若 和 都是从非空有穷集合 到非空有穷集合 的关系，则 当且仅当

• 关系图：（ 是 上的关系）顶点、有向边、自环

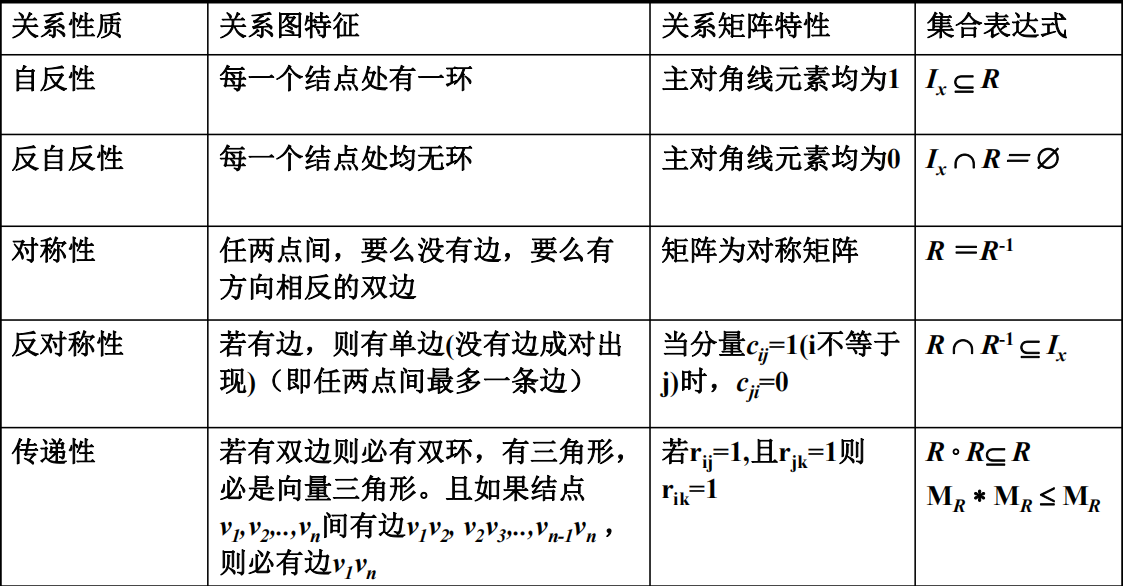
关系的性质

• 自反的：

  • 每个 都
  • 关系矩阵主对角线全为1
  • 关系图中每个顶点都有自环

• 反自反的：

  • 每个 都
  • 关系矩阵主对角线全为0
  • 关系图中每个顶点都没自环

• 既自反又反自反：空集上的空关系

• 既不自反又不反自反：集合 上的关系

• 对称的：

  • 每个 ，只要 ，就有
  • 关系矩阵是对称矩阵
  • 关系图中没有单向边（要么无弧要么两条相反方向的弧）

• 反对称的：

  • 每个 ，只要 且 ，就有
  • 
  • 关系矩阵中，若 ，则
  • 关系图中没有双向边（要么无弧要么一条弧）

• 既对称又反对称：只有自环的关系图，如

• 既不对称又不反对称：

• 传递的

  • 每个 ，只要 且 ，就有
  • 
  • 关系矩阵
  • 关系图中若从顶点 到顶点 有长度大于 1 的通路，则必有从 到 的有向边

6.2 关系的运算

• 
  尤其注意 是对称差集，其矩阵相应地做异或运算

• 复合关系：
  显然，

• 设 分别是从 到 ， 到 ， 到 的关系，则

• 的 次幂 ：
  

• 关系复合的矩阵运算

  • 
  • 若a到b有长度n的路径，则 有a到b的边

• 逆关系

  • 的关系矩阵是 的关系矩阵的转置矩阵
  • 设 R是从X到Y的关系, S是从Y到Z的关系, 则 。

• 闭包
  

  • 自反闭包：
    • 设 R 是集合 X 上的关系，则 R 的自反闭包
    • 是上的自反关系且
  • 对称闭包：
    • 设 R 是集合 X 上的关系，则 R 的对称闭包
    • 是上的对称关系且
  • 传递闭包：
    • 设 R 是集合 X 上的关系，则 R 的传递闭包
    • 设 R 是有 n 个元素的集合 X 上的关系，则
    • 是上的传递关系且

6.3 次序关系

• 偏序关系：自反+反对称+传递
  
  
  

• 严格偏序：反自反+传递
  
  
  

• 遮盖
  

• 哈斯图
  

• 最大元、最小元、极大元、极小元
  
  
  

• 上界、下界、上确界、下确界
  
  

• 良序集
  
  
  

6.4 等价关系

• 覆盖、划分
  
• 等价关系：自反、对称、传递
• 等价类
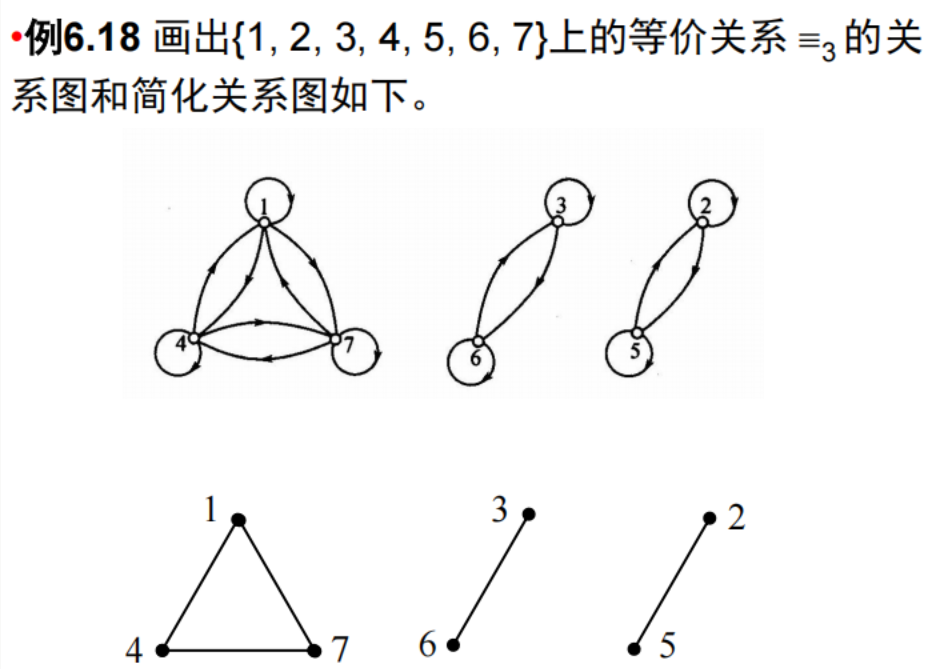
• 简图/简化关系图
  
• 等价与划分（商集、 ）
  
  • 集合X上的等价关系R与集合X的一个划分一一对应，集合X的不同划分，对应集合X上的不同的等价关系
  • 整数集I上的以m为模的同余关系是一种重要的等价关系
  • 给定非空集合X上的等价关系R，每一个X上的元素都有等价类，根据对称性和传递性，如果x和y有关系R，则它们生成的等价类是相同的；所有不同等价类构成的集合称为X关于R的商集，即X关于R的商集就是集合X的一个划分，商集中的每一个元素就是集合X的对应划分的一个块。
    

第7章 函数

1. 判断哪些是函数(2)；求函数(6)
2. 函数复合的计算(8)；函数复合的相关证明(10)
3. 证明单射/满射/双射(14 17)；多少中单射/双射(16)
4. 利用特征函数的性质证明等式
   

7.1 基本概念

• 函数：关系 满足单值性

• 从X到Y的函数
  
  ，即处处有定义
  是函数，即单值性

• 象、象源：对于函数 ， 为在 作用下 的象， 为 的一个象源。

• 常用函数

  • 恒等函数：
  • 后继函数：
  • 地板函数：
  • 天花板函数：

• 限制与开拓：设函数 ，又 ，则 是从 到 的函数，称为 受限制于 ，记为 ，又称 为 的开拓。
  只是去掉那些以不在 中的元素为第一元的有序偶，将定义域改为 。

• 象：设函数 ，。称集合 为 在 下的象，记为 。

  • 显然，整个定义域的象 成为函数 的象，即 的值域，也即：。
  • 由函数 派生出函数 。

• 从X到Y的偏函数(不要求定义域为整个X)：设 是从集合 到 的关系。若对每个 存在唯一 使得 ，则称 为从 到 的偏函数，又称为部分函数

  • 是从集合 到 的函数当且仅当
    • 为从 到 的偏函数

• Y上X：用 表示所有从 到 的函数组成的集合，即 ，读作“ 上 ”

  • 若 和 都是有穷集合，则
  • 设 ，，则 可有 种选择，所以
  • 对于任意集合 ，
  • 若 是非空集合，则
  • 设 是全体命题变元组成的集合，则 是全体真值赋值组成的集合。

• 函数和一般关系的差别（对于有限集合 ）

  • 集合个数存在差别：从 到 的不同关系共有 个，从 到 的不同函数有 个
  • 集合的基数（集合内元素的个数）存在差别：每一个关系的基数可以从 一直到 ，每一个函数的基数都为 个
  • 集合元素的第一元存在差别：关系的第一元可以相同，函数的第一元一定互不相同。

7.2 函数的复合

• 若 且 ，则函数的复合 是一个从 到 的函数，即 ，且对所有的 ， 。

• f的n次复合；设 ， 定义如下：

• 多元函数：若函数 的定义域是 个集合的笛卡尔乘积，则称 为 元函数，并将 记为

  • 若 ，则称 为 上的二元运算，常采用中缀记法，将 记为 ，如实数加法 。

7.3 特殊性质的函数

• 设函数

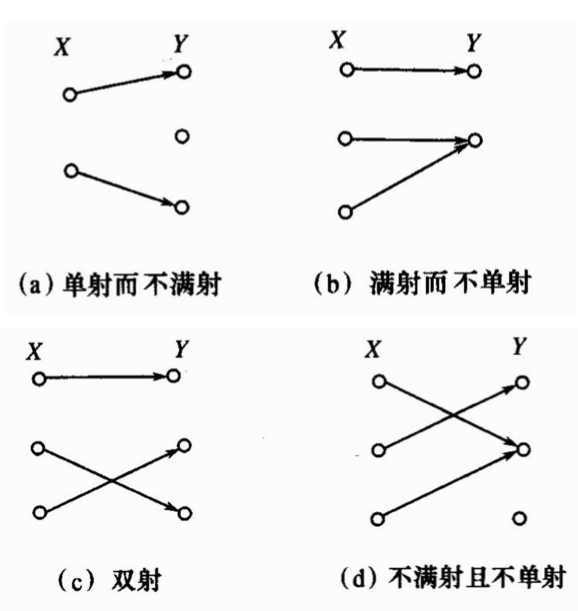
  • 满射：
  • 单射：即只要 ，就有
  • 双射/一一对应：即是单射又是满射
  • 具有上述特性的函数分别称满射函数，单射函数，双射函数。
    

• 对于实函数 ，即 ，可以通过 的图像判断 是不是满射、单射、双射

  • 是满射当且仅当，每条与横轴平行的直线与 的图像至少有一个交点。
  • 是单射当且仅当，每条与横轴平行的直线与 的图像至多有一个交点。
  • 是双射当且仅当，每条与横轴平行的直线与 的图像恰好有一个交点。

• 设 是从 到 的函数， 是从 到 的函数

  • 若 和 都是满射，则 是满射。
  • 若 和 都是单射，则 是单射。
  • 若 和 都是双射，则 是双射。

• 常值函数：

• 关于逆函数

  • 若 单射，则 单值。
  • 若 满射，则 处处有定义。
  • 定理7.4：若 双射，则 也是双射函数。若 不双射，则 不是函数

• 反函数：设 是双射函数，称 的逆关系 为 的反函数。

• 可逆：设 ，如果存在 使得 且 ，则称 为可逆的。

• 定理7.5：若 是双射，则 且

• 定理7.6：设双射 及双射 ， 当且仅当 且 。
  

• 定理7.7：若双射 及双射 ，则 也是双射，并且

• 补充：双射集合构成群
  设 是所有从 X 到 X 的双射函数组成的集合

  • 封闭性：对于任意 ， 和 都。（此性质也称为复合运算的闭包性）
  • 结合律：对于任意 ，
  • 有单位元：，对于任意 ，
  • 有逆元：对于任意 ，存在反函数 ，
    是群

7.4 集合的特征函数

• 特征函数 ： 设 是全集 的子集， 的特征函数 定义为
  若若
• 设 是全集 的任意两个子集，则对于所有 ，下列关系成立
  • 
  • 

图论

第9章 基本概念

9.1 有向图及无向图

• 有向图 (digraph)、无向图 、有限图、带权图

9.2 图的基本结构

• 关联、相邻、邻接

  • 点和点：邻接
  • 点和边：关联
  • 边和边：相邻

• 简单图

  • 自环
  • 在有向图中，始点和终点分别相同的两条弧称为平行弧。在无向图中，两个顶点之间的两条边称为平行边。
  • 有平行弧的有向图称为多重弧图，有平行边的无向图称为多重边图。多重弧图和多重边图统称为多重图。
  • 无自环和平行弧（或平行边）的图称为简单图。
  • 对于简单有向图 ， 是 上的反自反关系(因为不存在自环)，它的图形表示是 的关系图。

• 顶点的次数(degree)

  • 引出弧、引入弧
  • 引出次数、引入次数（有向图）
  • 次数（有向图、无向图）：因为无向图中与 关联的自环的两个端点都是 ，所以应将自环计为两条边。
  • 孤立点：次数为 0 的顶点
  • 悬挂点：次数为 1 的顶点
  • 悬挂边：与悬挂点关联的边
  • 零图：每个顶点都是孤立点的图
  • 平凡图：1 阶零图，即仅由一个孤立点构成的图称为平凡图

• 握手定理

  • 对于顶点集合为 的 有向图，
  • 对于顶点集合为 的 有向图，
  • 次数为奇数的顶点称为奇顶点，次数为偶数的顶点称为偶顶点。
  • 在任何图中，奇顶点的个数必为偶数。

• 正则图：无向图 的所有顶点的次数都是同一个数 ，则称 为 次的正则图。

• 无向完全图
  任何两个顶点之间都有一条边的简单无向图称为完全图，将 n 阶完全图记为 。 是 次正则图，它的边数为

• 有向完全图
  任意两顶点之间都恰有一条弧的简单有向图称为有向完全图，也称为竞赛图。在 阶有向完全图中，每个顶点的次数都是 ，边数为 。

• 图的同构

  • 无向图：设 和 是两个无向图。若存在双射 使得， 当且仅当 ，并且重数相同，则称 和 是同构的。
  • 有向图：设 和 是两个有向图。若存在双射 使得， 当且仅当 ，并且重数相同，则称 和 是同构的
  • 性质（必要但不充分）
    • 同样的顶点数。
    • 同样的边数。
    • 对于任意自然数 ，次数为 的顶点数一样多。
    • 有同样多的自环。

9.3 子图

• 子图/部分图、真子图

• 补图：设 和 是图 的两个子图。若 ，并且 与关联是中孤立点，则称 为 相对于 的补图。

• 无向图

  • 导出子图：（点不一定全，边也不一定全，但只要两边的点都有就一定有边）设 是 的子图。若 的端点都在中，则称 为 的由 导出的子图，或简称 的导出子图。
  • 生成子图：（只要求点是全的，边不一定全）设 是 的子图。若 ，则称 为 的生成子图。
  • 去点运算、去边运算
  • 加法运算：设无向图 中顶点 和 不相邻，在 中增加边 得到的图记为 。
  • 图的并集

• 有向图的导出子图：（点不一定全，边也不一定全，但只要两边的点都有就一定有边）设 ＝ 是有向图 的子图，如果 的各条弧是由 的所有在 中拥有始点和终点的那些弧所组成，即 的始点和终点都在中，则称 为顶点集合 所导出的子图，或简称图 的导出子图。

9.4 连通性

9.4.1 有向图 通路 回路 连通

• 通路：在有向图 中，首尾相接的弧的序列 称为通路。

• 长度

• 简单通路：无重复边

• 基本通路：无重复点

• 基本通路必是简单通路，简单通路未必是基本通路。

• 回路：（一圈）始点终点相同

• 简单回路：一圈+无重复边

• 基本回路：一圈+除了始点终点无重复点

• 无回路图：没圈

• 半通路（有边）、通路（有同向边）

• u连接到v、u可达v（从 到 有“正向”边）：若存在从顶点 到顶点 的半通路，则说 连接到 。若存在从顶点 到顶点 的通路，则说 可以到达 。
  可达关系是顶点集 上的自反的、传递的关系。

• 若从顶点 可以到达顶点 ，则存在从 到 的基本通路。

• 到 有通路，则必有基本通路，且最短通路必是基本通路；从而 到 无基本通路，则必无通路

• 从u到v的距离

  • 当且仅当
  • （三角不等式）
  • 在 阶有向图中，任何基本通路的长度都不超过 ，任何基本回路的长度都不超过 。
    从到的最短通路的长度从可到达

• 强联通的、3度连通的：（任意两点互相可达）

• 单向连通的、2度连通的：（任意两点至少一个方向可达）

• 弱连通的、1度连通的：（任意两点互相连接）

• 不连通的、0度连通的：（不弱连通）

• 完备通路：称通过有向图中所有顶点的通路为完备通路。

• 完备回路：称通过有向图中所有顶点的回路为完备回路。

• 完备半通路：称通过有向图中所有顶点的半通路为完备半通路。

• 有向图 是强连通的当且仅当 有一条完备回路。

• 有向图 是单向连通的当且仅当 有完备通路。

• 有向图 是弱连通的当且仅当 有完备半通路。

9.4.2 无向图 链 连通

• 链、长度
• 简单链：（各边不同）
• 基本链：（各点不同）
• 闭合链：（第一个点和最后一个点相同）
• 圈：（第一个点和最后一个点相同且各边不同）
• 从u到v的距离
  • （对称性）
  • （三角不等式）
  • 当且仅当
    从到的最短通路的长度从可到达
• 连通：有链
• 图的连通：若无向图 中任何两顶点都是连通的，则称 是连通的，否则说 是不连通的。
• 连通分支：无向图 的顶点之间的连通关系是等价关系。每个等价类是顶点集的一个非空子集。由等价类导出的子图称为 的连通分支，等价类的数目即连通分支的数目。
  图 是连通的当且仅当 只有一个连通分支。
• 割点：设 是连通无向图 的顶点，如果从 中去掉 和与它关联的边得到的无向图 是不连通的，则称 为 的割点。
• 割边/桥：设 是连通无向图 的边，如果从 中去掉 得到的无向图 是不连通的，则称 为 的割边或桥。

9.5 顶点基和强分图

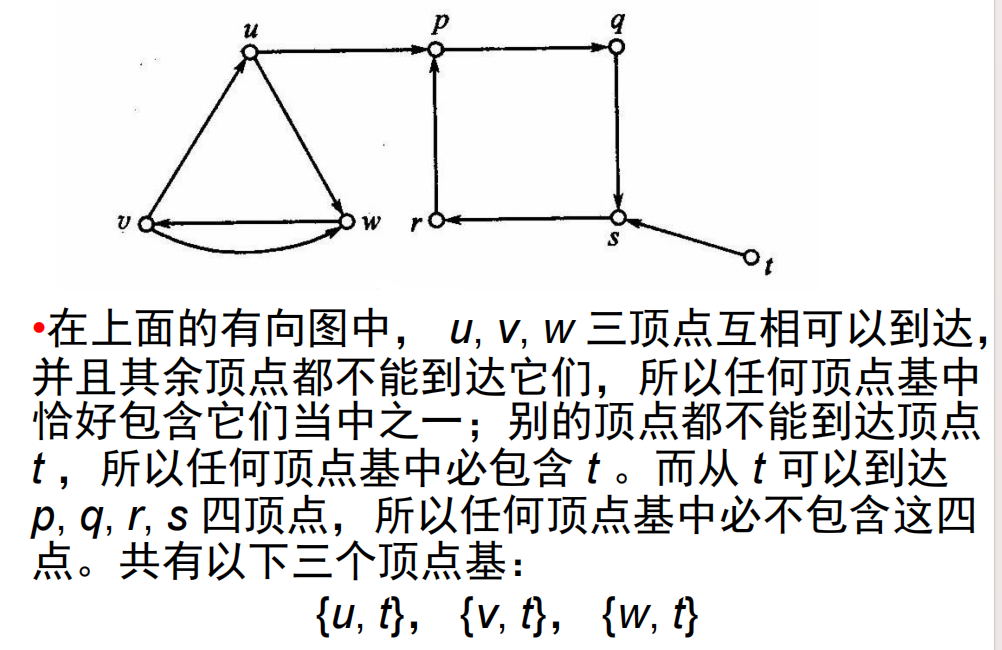
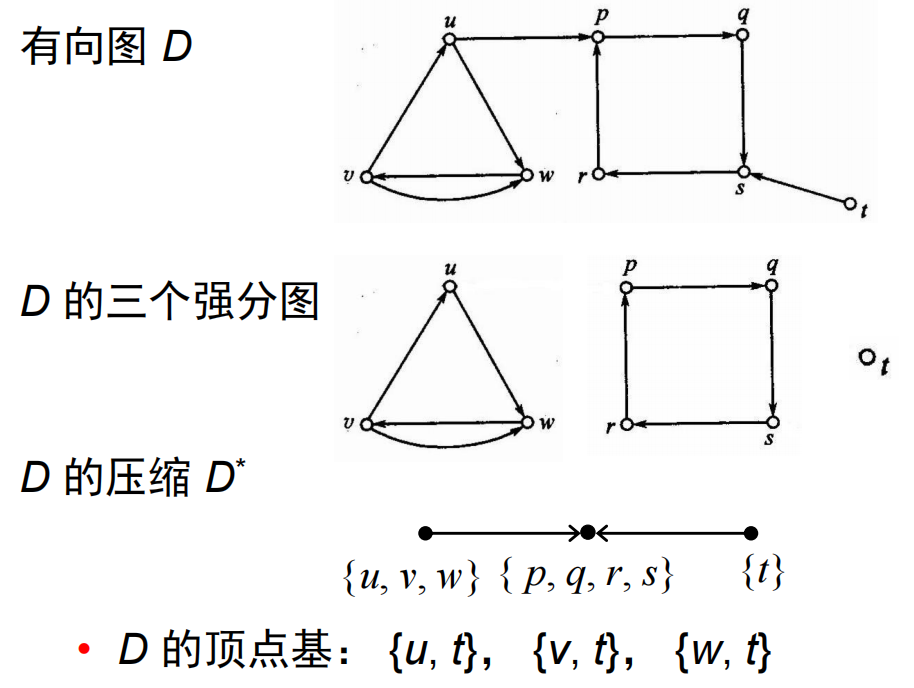
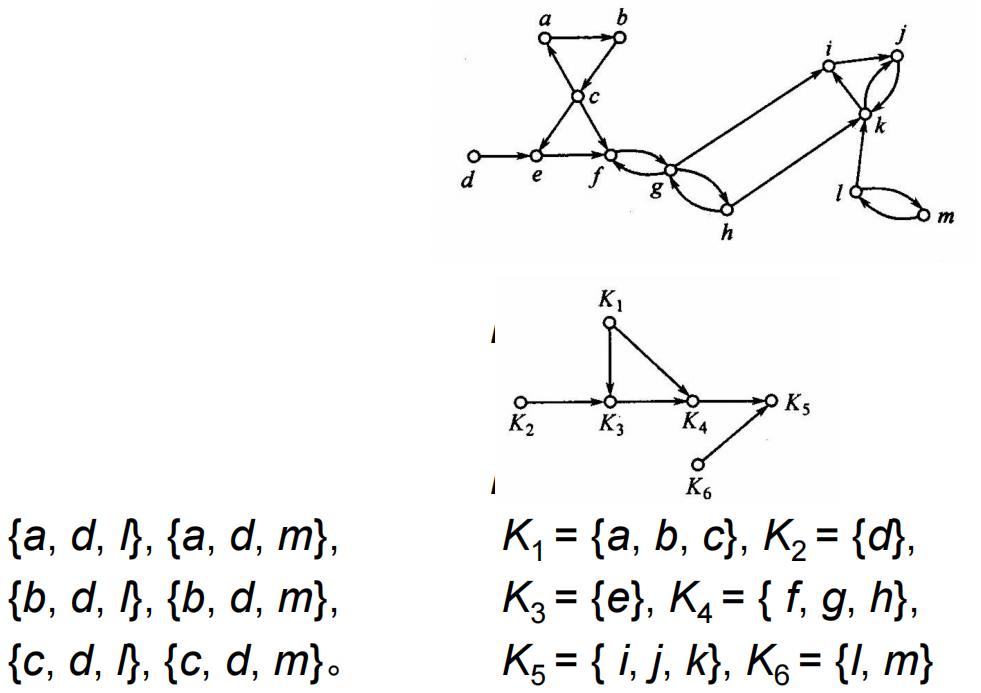
9.5.1 顶点基

• 设有向图 ， ， 。若从 中某个顶点可以到达 ，则称从 可以到达 。
• 顶点基：（可达所有点且极小）设有向图 ，。若从 可以到达 中每个顶点（相当于 可以到达 中的每个顶点，因为 中的点可以到达自身），并且 的每个真子集都不能到达 中每个顶点，则称 为 的顶点基。
  

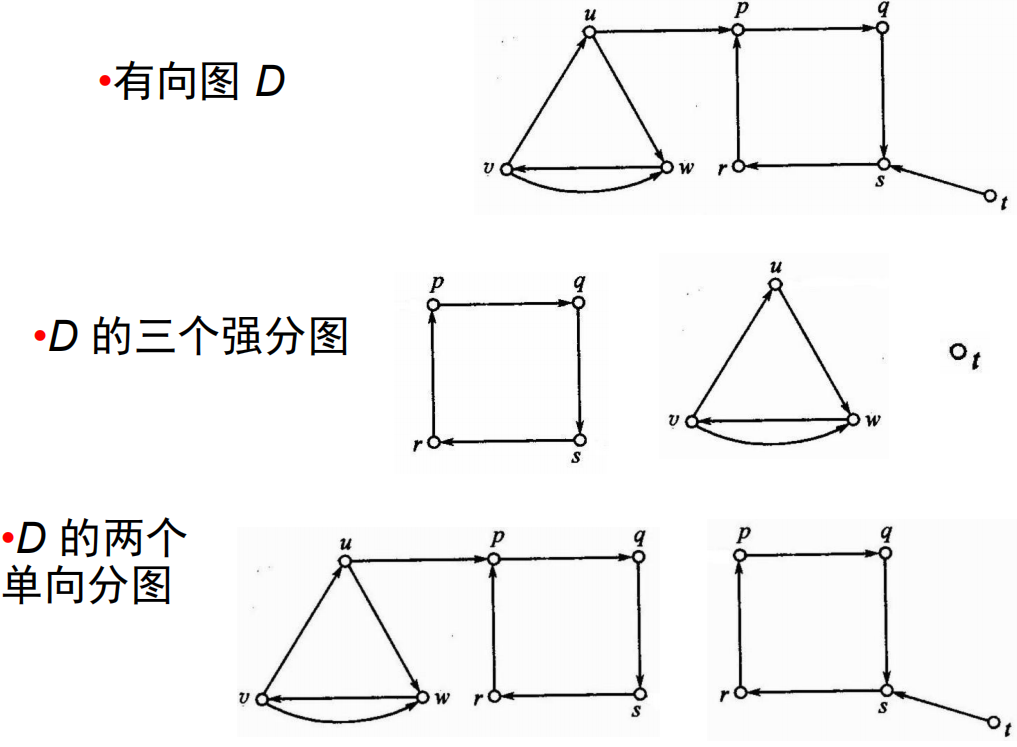
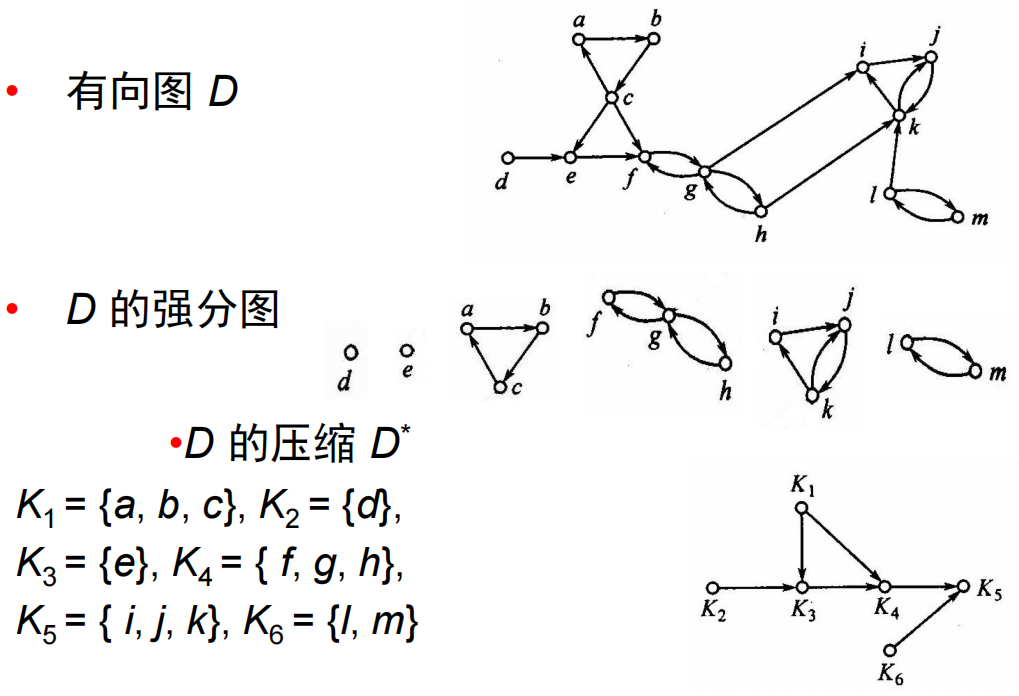
9.5.2 强分图

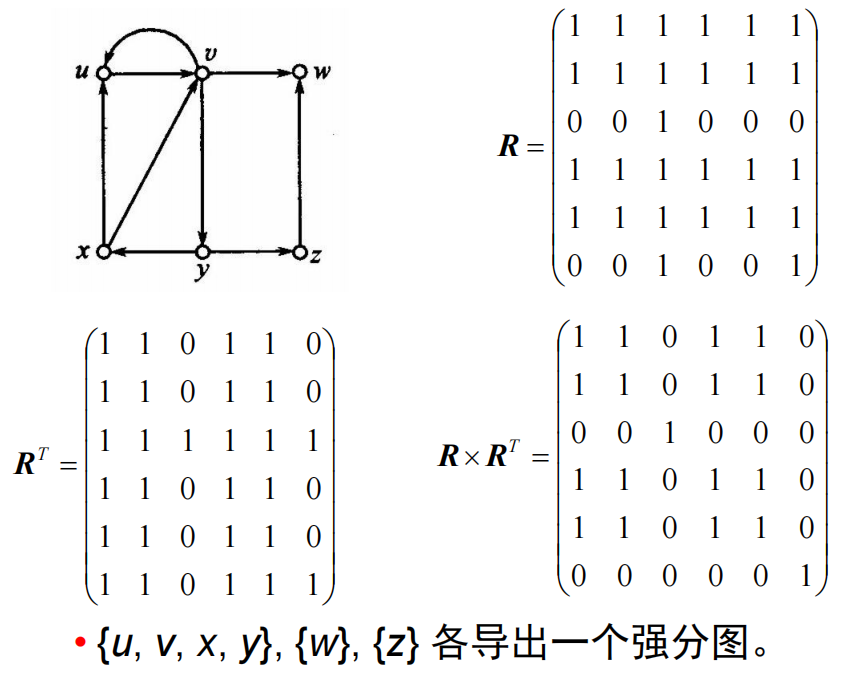
• 强分图：（极大的强连通子图）设 是有向图。若 是 的强（单向、弱）连通子图，并且对于 的任意强（单向、弱）连通子图 ，若 ，则 ；那么就称 为 的强（单向、弱）连通分图，或强（单向、弱）分图。
• 定理9.8：在有向图 中，每个顶点在唯一的强分图中，每条弧至多在一个强分图中。
  • 即在一个有向图中没有不在强分图中的顶点；任意两个强分图都没有公共顶点
  • 若弧 在两个强分图中，则它的端点在两个强分图中。
    

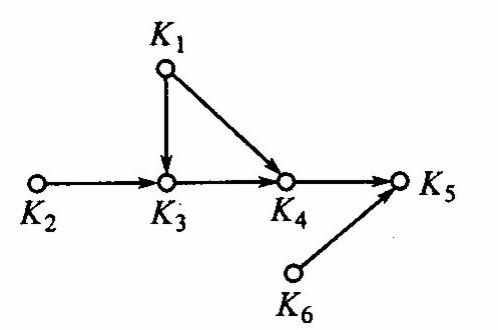
9.5.3 压缩

• 压缩：（强分图之间的弧组成的图）设有向图 的强分图的顶点集为 ，有向图 定义为 ，
  
• 定理9.9：有向图 的压缩 是无回路图。
• 定理9.10：无回路有向图（如压缩） 有唯一的顶点基，它由所有引入次数为 0 的顶点组成。
  
• 定理9.11：（压缩的顶点基中每个元素取出一个顶点可以构成原图的顶点基）设 是有向图 的压缩， 是 的唯一顶点基，则从 的每个元素中取出一个顶点构成的集合 是 的顶点基，并且 的每个顶点基都可以这样得到。
• 定理9.12：有向图 的每个顶点基都包含同样数目的顶点。
  
  

9.6 总结

• 根据图的结构特点，定义出多种图的名称
  无向图、有向图、带权图、邻接、关联、相邻、自环、平行弧/边、多重图、简单图、次数、n阶图、零图、平凡图、完全图
• 对于图和图之间的比较，定义出多种图的名称
  补图、正则图、同构图、子图(生成子图和导出子图)、图的并集
• 考察不相邻节点之间的关系，定义出新的概念
  通路及回路、简单通路及回路、基本通路及回路、可达、半通路、连接到、强(单向/弱)连通、完备通路(回路/半通路)、链、简单链、基本链、闭合链、圈、连通分支
• 根据连通图中特殊点和边的特点，定义出新的概念
  割点、割边/桥、顶点基、强分图(单向分图/弱分图)、压缩

第10章 通路问题

10.1 最短通路

• 弧 的长度 、通路 的长度 、从 到 的最短通路、从 到 的距离

10.2 关键通路

• 工序流线图是满足以下条件的简单带权有向图：

  • 没有回路。
  • 有唯一的引入次数为 0 的顶点，称其为发点。
  • 有唯一的引出次数为 0 的顶点，称其为收点。
  • 每个顶点都在某条从发点到收点的通路上。
  • 每条弧的权是非负实数。

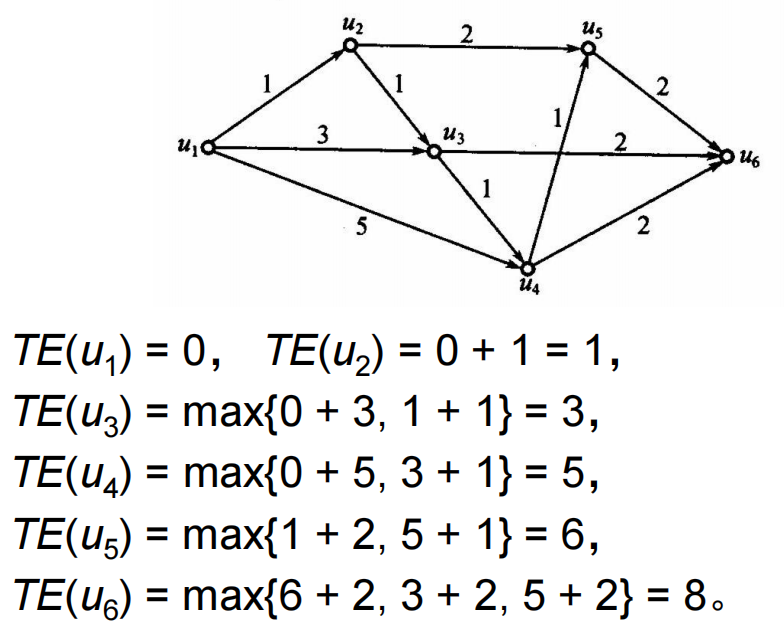
• 最早完成时间：在工序流线图中，从发点 到事件 的最长通路的长度称为事件 的最早完成时间，记为 。
  
  
  

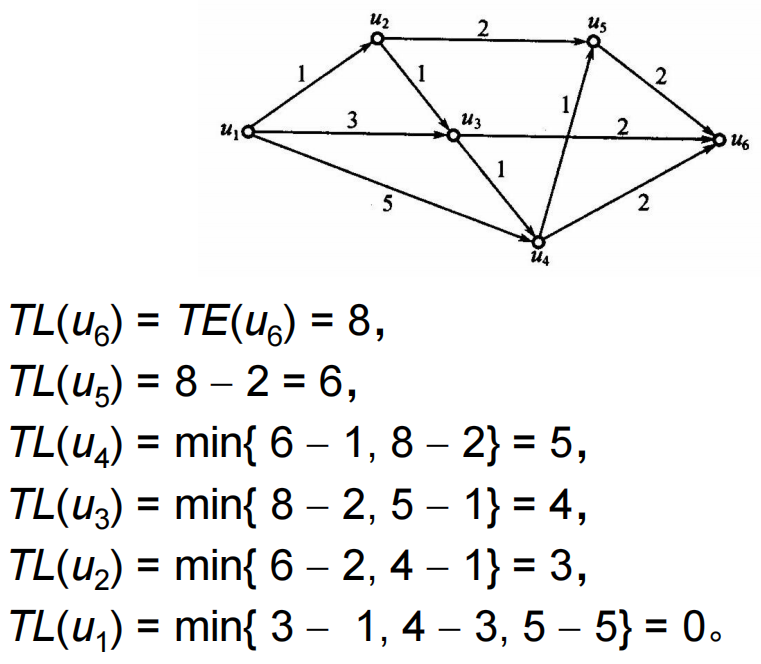
• 最迟完成时间：给定工序流线图，在保证收点 的最早完成时间不增加的前提下，自发点 最迟到达事件 的时间称为 的最迟完成时间，记为 。
  
  
  

• 关键通路：在工序流线图中，从发点到收点的最长通路称为关键通路。

• 事件 在某条关键通路上当且仅当它的最早完成时间和最迟完成时间相等。

• 缓冲时间：给定工序流线图 ，，定义 的缓冲时间 。

  • 事件 的发生可以比预定的最早完成时间推迟缓冲时间 ，而不会影响整个工程的进度。
  • 关键通路上的所有事件的缓冲时间都是0，即它们都要准时发生，不能推迟，并且关键通路上的工序都要按时完成，不能推迟。

第11章 图的矩阵表示

11.1 邻接矩阵

11.1.1 有向图的邻接矩阵

• 对于简单有向图 来说，邻接矩阵 M 为 A 的关系矩阵。
  因为简单图没有自环，所以邻接矩阵 M 的主对角线全为 0。

• 定理11.1：设 是有向图，， 是 的邻接矩阵，，则 是从顶点 到顶点 的长度为 的通路的条数。

  • 是 到 的最短通路的长度，所以其是使 中第 行第 列的元素有非零值的最小正整数
  • 对于 和 ＝，如果 中第 行第 列的元素均为0，又结合定理9.4（任何基本通路的长度不超过n-1），则可得从 到 不存在任何通路，因而属于不同的强分图。

11.1.2 无向图的邻接矩阵

• 特别地，对于简单无向图来说
  简单无向图G 的邻接矩阵M 是对称矩阵
  主对角线元素都是0

• 定理11.2：设 是无向图，， 是 的邻接矩阵，，则 是从顶点 到顶点 的长度为 的链的条数。

11.2 有向图的可达性矩阵

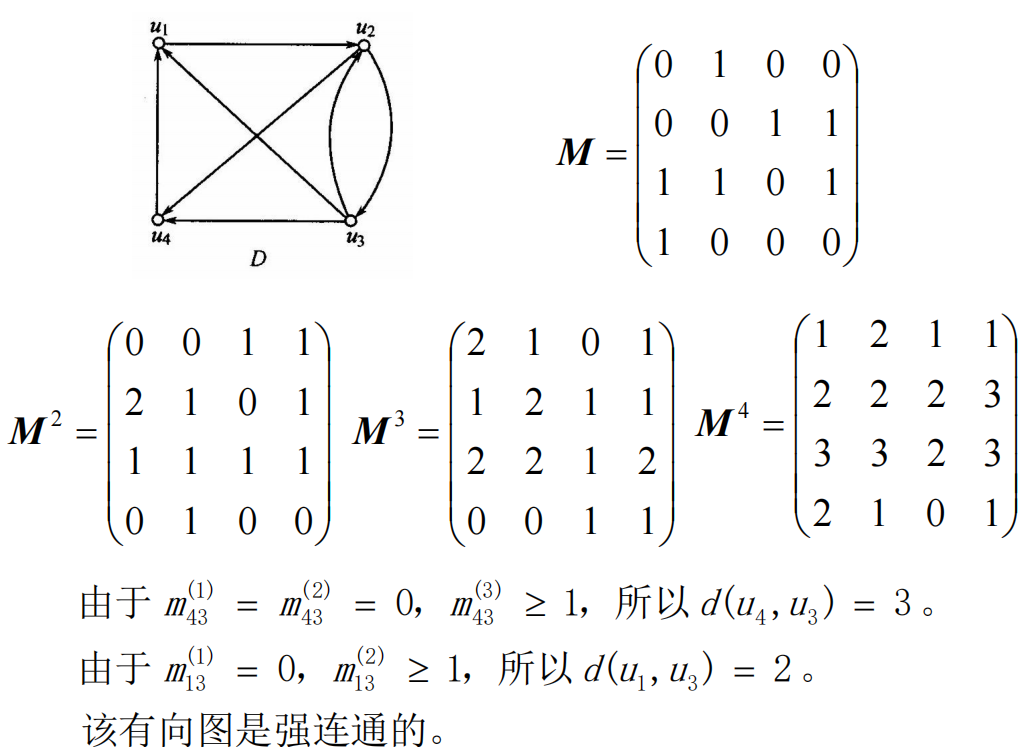
• 可达性矩阵：设有向图 ，， 的可达性矩阵 定义为

  若可达否则

  因为每个顶点可以到达自己，所以任何有向图的可达性矩阵的主对角线元素全为1
  设 和 分别是 阶有向图 的可达性矩阵和邻接矩阵，则，其中 是 阶单位矩阵。

• 布尔函数

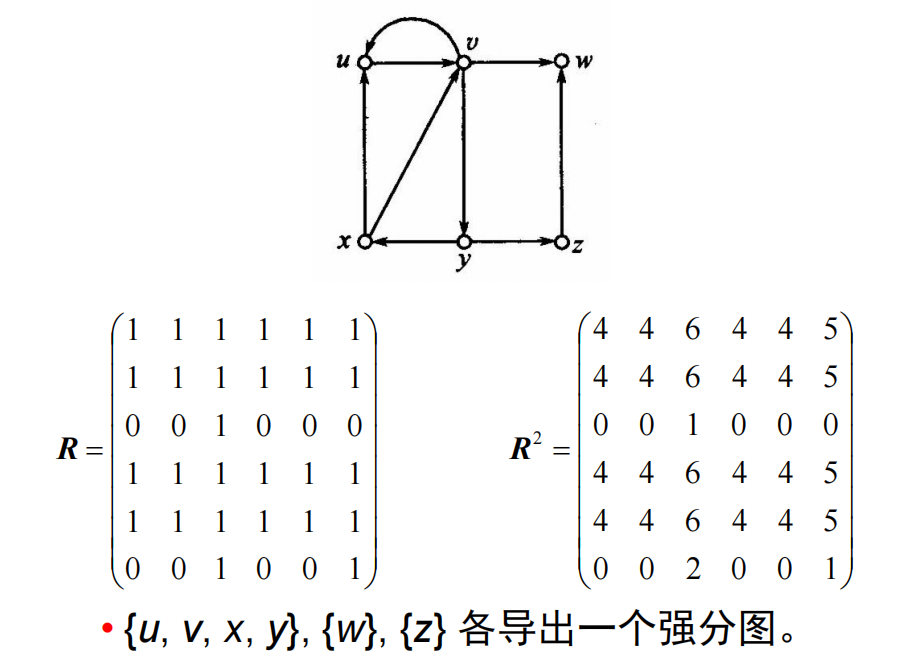
• 可达矩阵的应用：求包含指定顶点的强分图以及此强分图中所含顶点的数目。

• 元素积：设 且 ，称 为 和 的元素积。

• 定理11.4：设 是有向图 的可达性矩阵，并设 ，则

  • 由 的第 i 行（列）中等于 1 的元素对应的顶点导出的子图是 所在的强分图。
    解释： 的 表示 i 可达 j， 的 表示 j 可达 i，故 中 的表示 i j 互达
  • 所在的强分图有 个顶点。
    与 互达的顶点数
    
    

• 设 R 和 M 分别是 n 阶有向图 D 的可达性矩阵和邻接矩阵，则

  • 是强连通的当且仅当 的元素全为 1。
  • 是单向连通的当且仅当 的元素全为 1。
  • 是弱连通的当且仅当 的元素全为 1，其中 。
  • 是无回路的当且仅当 的主对角线元素全为 0。

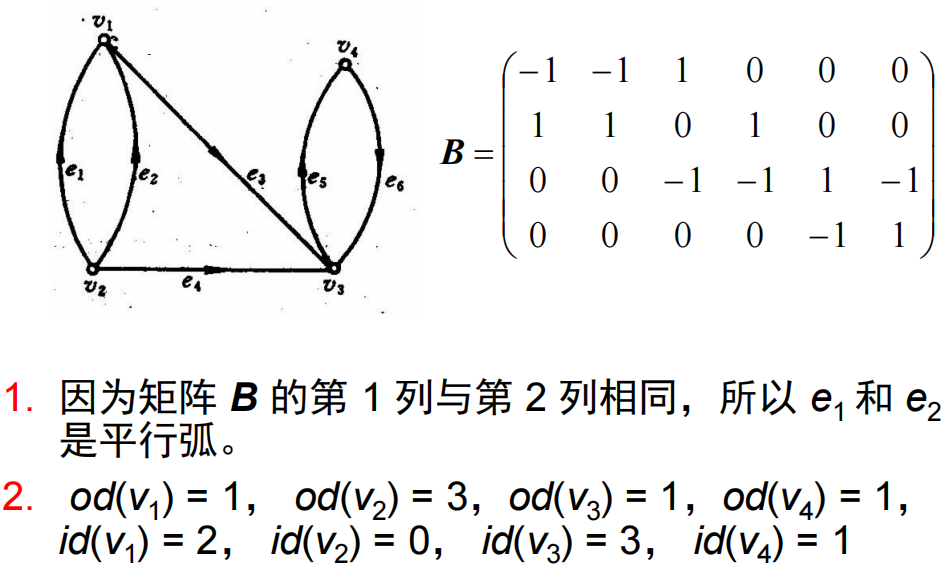
11.3 关联矩阵(Incidence Matrix)

11.3.1 有向图的关联矩阵

• 关联矩阵：设无自环有向图 不是零图，其中 ，， 的关联矩阵 定义为
  若是弧的始点若是弧的终点若不是弧的端点
  矩阵 每列元素之和都是0。
  若 的第 i 列与第 j 列相同，则 和 是平行弧。
  的第 i 行中 1 的个数 = 顶点 的出度，
  的第 i 行中 −1 的个数 = 顶点 的入度。
  

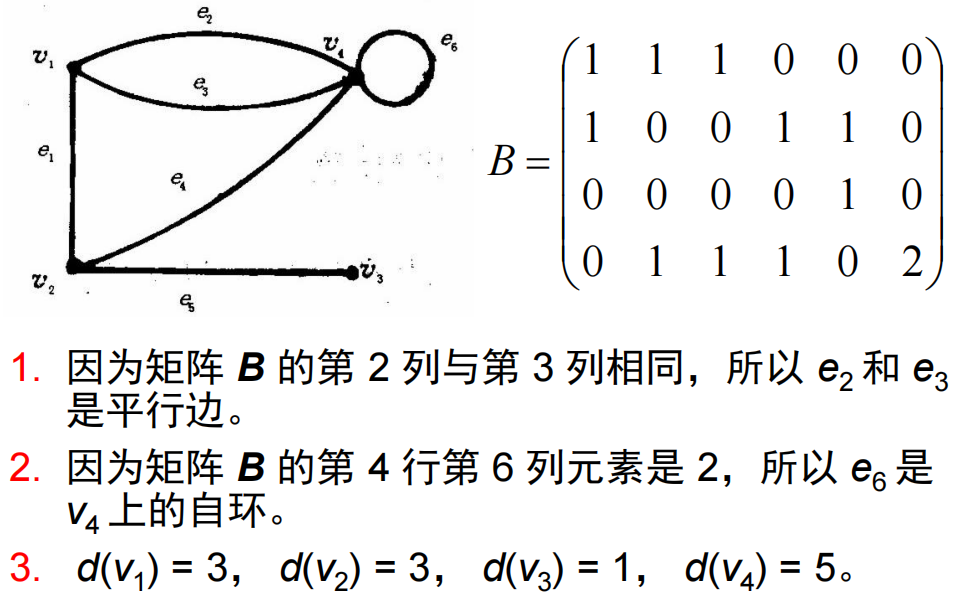
11.3.2 无向图的关联矩阵

• 关联矩阵：设无自环有向图 不是零图，其中 ，， 的关联矩阵 定义为
  与的关联次数
  矩阵 每列元素之和都是 2
  若 的第 i 行第 j 列是 2，则 是 上的自环
  若 的第 i 列与第 j 列相同，则 和 是平行弧
  的第 i 行元素之和 = 顶点 的度
  

第12章 树

12.1 树的一般定义

• 树：连通且无圈的无向图称为树。

• 林：无圈的无向图称为林。林是每个连通分支都是树的无向图。

• 树的等价定义
  设 是 无向图。以下说法是等价的。

  • 连通且无圈。
  • 无自环，并且每对顶点之间有唯一基本链。
  • 连通，在 中加一边仅有一个圈。
  • 连通，去掉任何一边就不连通了。
  • 连通，并且 。
  • 无圈，并且 。

• 树叶、分支顶点

• 定理12.3：非平凡树中至少有两片树叶

12.2 根数与有序树

• 有向树：将一个树的边加上任意的方向，就得到有向树。任何有向树都是弱连通的无回路有向图，但是弱连通的无回路有向图未必是有向树（如下图）。
  

• 树根、根数：若有向树 T 有一个顶点的引入次数为0，其余顶点的引入次数都为 1，则称 T 为根树。称根树中引入次数为 0 的顶点为树根。

• 树叶、分支顶点、级：从树根到一个顶点的通路的长度称为该顶点的级。

• 树高：根树中顶点的级的最大值称为树高

• 有序树：称为顶点或弧指定了次序的根树是有序树。若从顶点 u 可以到达 v ，则称 v 为 u 的后裔， u 为 v 的祖先。若 < u, v > 是弧，则称 v 为 u 的儿子，u为 v 的父亲，同一顶点的儿子互为兄弟。

12.3 二元树

• m元树、完全m元树、位置m元树
  • 每个顶点的引出次数都小于等于 m 的根树称为 m 元树。
  • 每个顶点的引出次数都等于 m 或 0 的根树称为完全 m 元树。
  • 若为 m 元树 T 中每个顶点的各儿子规定了位置，则称 T 为位置 m 元树。

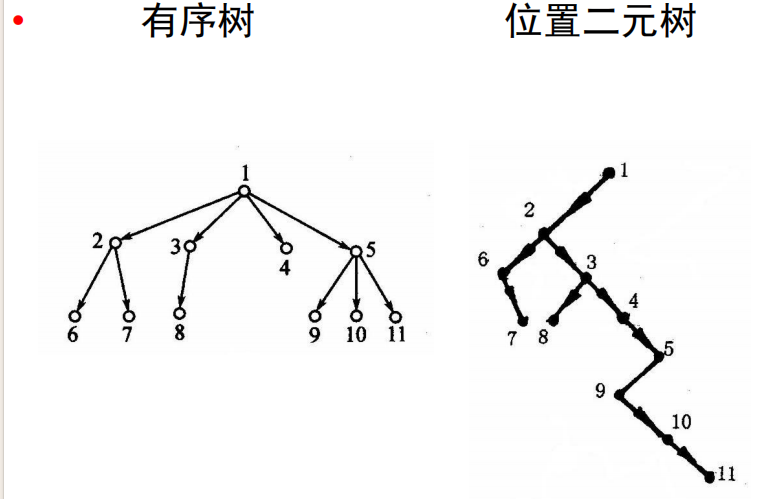
有序树转换为位置二元树的算法

• 若 u 是原来有序树的树根，则它仍然是转换后的位置二元树的树根。

• 在原来有序树中，

  • 若顶点 u 是 v 的大儿子，则在转换后的位置二元树中，u 是 v 的左儿子；
  • 若顶点 u 是 v 的大兄弟，则在转换后的位置二元树中，u 是 v 的右儿子。
    

• 每个弱分图都是有序树，并且为各有序树规定了顺序的有向图称为有序林。如果称排在前面的有序树的树根是排在后面的有序树的树根的哥哥，并规定转换后的位置二元树的树根是有序林中第一个有序树的树根，则可按照上面的算法将有序林转换为位置二元树。

前缀码

• 若存在非空符号串 使得 ，则称符号串 是符号串 的前缀。设 A 是字母表 {0, 1} 上的语言，若不存在 , A 使得 是 的前缀，则称 A为二元前缀码。
  例如，{00, 10, 11} 是二元前缀码， {1, 00, 10, 11} 不是二元前缀码
• 二元树和二元前缀码
  让位置二元树中的每个顶点对应一个 {0, 1} 上的字，令所有树叶对应的字的集合为该位置二元树产生的二元前缀码。
  • 顶点对应的字归纳定义如下：
    • 树根对应空字 。
    • 若顶点 u 对应字 ，则 u 的左儿子对应 ， u 的右儿子对应 。
  • 每个顶点对应字的长度等于该顶点的级。从顶点 u 可以到达另一顶点 v 当且仅当 u 对应的字是 v 对应的字的前缀。因为从一个树叶不可能到达另一树叶，所以位置二元树产生的语言是二元前缀码。反之，任意二元前缀码都可由一个位置二元树产生。

最优二元树

• 带权二元树 的权 、最优二元树。
• 设 ，则存在一个带权 的最优二元树使得权为 和 的树叶是兄弟。
• 设 ， 是带权 的二元树。为 中带权 的树叶增加两个分别带权 的儿子得到带权 的二元树 。那么， 是带权 的最优二元树当且仅当 是带权 的最优二元树
• Huffman算法
  

12.4 生成树

• 若无向图 G 的生成子图 T 是树，则称 T 为 G 的生成树。

• 设 T 是无向图 G 的生成树。称 T 中的边为 T 的树枝，称 G 的不在 T 中的边为 T 的弦，弦的集合称为 T 的补。(n, m) 无向图 G 的任何生成树有 n − 1 个树枝，m − n + 1 条弦。当然， G 的某条边可能是这棵生成树的树枝，却是另一棵生成树的弦

• 定理12.7：无向图 G 有生成树当且仅当它是连通的。

• 基本圈、基本圈组：(n, m) 无向图 G 的生成树 T 有 m − n + 1 条弦。任取 T 的一条弦 e ， T + e 有唯一的圈，它由树枝和弦e 组成，称这样的圈为对应于弦 e 的基本圈。由这 m− n + 1 个基本圈组成的集合称为关于生成树 T 的基本圈组。
  

最小生成树

12.5 割集

• 割集(最小的 能把图分成两块的边的集合)：设连通无向图 ，。若 不连通，即 分离成为两个连通分支，并且对于任意 ， 仍然连通，则称 为 的割集。
  割集的等价定义： 是连通无向图 的割集当且仅当存在 的划分 使得 ，并且 导出的子图和 导出的子图都是连通的。

• 桥： 是 中的桥当且仅当 是 的割集。

• 基本割集(一个树枝一堆弦)、基本割集组：设 是 连通无向图 的生成树。因为从 中去掉所有弦后仍连通，所以每个割集中必有树枝。因为从 中去掉所有弦和一个树枝后不再连通，所以，对于每个树枝都存在由它和若干弦组成的割集。我们称只包含一个树枝的割集为基本割集。显然，有 n −1个基本割集。称由这 n −1 个基本割集组成的集合为关于生成树 的基本割集组。

• 定理12.8：每个圈与任何生成树的补(即弦的集合)至少有一条公共边，即每个圈中都包含弦。

• 定理12.9：每个割集与任何生成树至少有一条公共边，即每个割集中都包含树枝。

• 定理12.10：任何圈和任何割集都有偶数条（包含零条）公共边。

• 定理12.11：给定图 的生成树 。设 是基本割集，其中 是树枝， 是弦，则 包含在对应于 的基本圈(一个弦一堆树枝)里，但不包含在任何其它基本圈里。

• 定理12.12：给定图 的生成树 。设 是基本圈，其中 是弦， 是树枝，则 包含在对应于 的基本割集(一个树枝一堆弦)中，但不包含在任何其它基本割集中。

第13章 穿程问题

13.1 欧拉图

无向图中的欧拉图

• 欧拉圈、欧拉图：称穿过无向图中每条边的简单闭合链为欧拉圈。有欧拉圈的图称为欧拉图。
• 若无向图 中每个顶点的次数大于1，则在 中存在圈。
• 定理13.1：连通无向图 是欧拉图当且仅当 的每个顶点都是偶顶点。
• 欧拉链：称穿过无向图 中每条边的简单非闭合链为欧拉链。(注意：欧拉链一般不是基本链)
• 定理13.2：在连通无向图 中存在连接顶点 和 的欧拉链当且仅当只有 和 是奇顶点。
  

一笔画问题

从无向图的一个顶点出发，笔不离纸，不重复地画出该图的所有边。

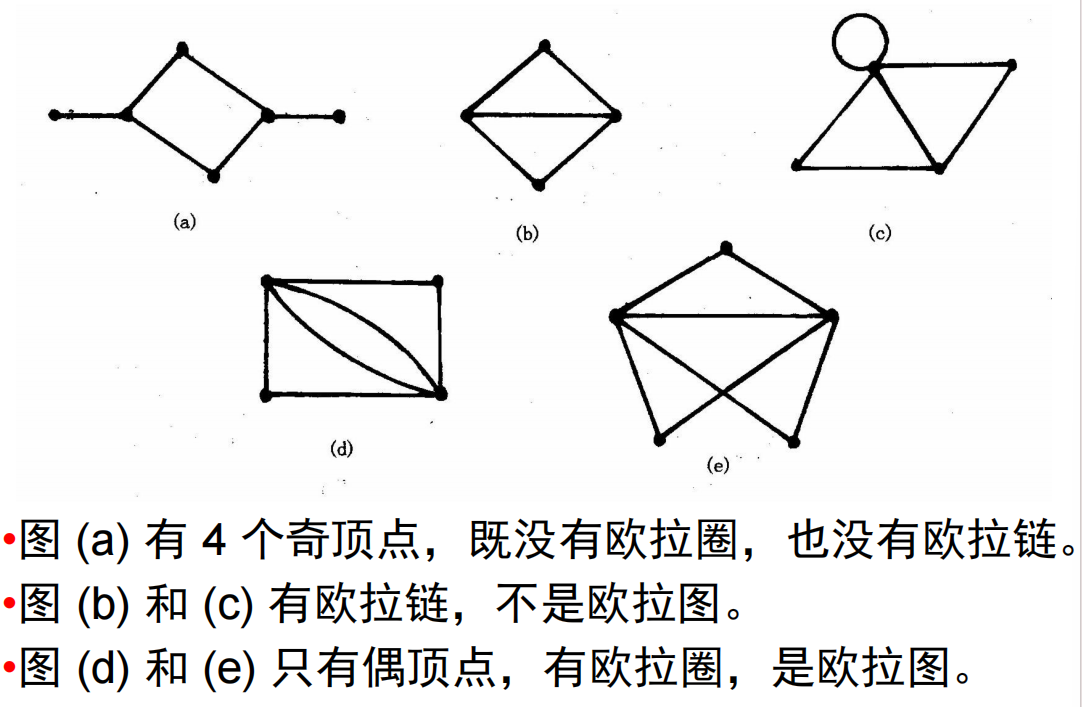
• 若连通无向图只有偶顶点，则从任意顶点出发，可沿欧拉圈不重复地一笔画出所有边，并回到出发点。
• 若连通无向图只有两个奇顶点，则从一个奇顶点出发，可沿欧拉链不重复地一笔画出所有边，并到达另一个奇顶点。
• 若连通无向图有多于两个奇顶点，则不能不重复地画出该图的所有边。

有向图中的欧拉图

• 欧拉回路、欧拉图：称穿过有向图中每条弧的简单回路为欧拉回路。有欧拉回路的有向图称为欧拉图。
• 欧拉通路：称穿过有向图中每条弧且非闭合的简单通路为欧拉通路。
• 强连通有向图 是欧拉图当且仅当 中每个顶点的引入次数与引出次数相同。
• 单向连通有向图 有从顶点 到 的欧拉通路当且仅当 的引出次数比引入次数大1， 的引入次数比引出次数大1， 中其它顶点的引入次数与引出次数相同。
  
  
  

13.2 哈密顿图

• 哈密顿圈、哈密顿回路、哈密顿图

  • 称穿过无向图 中每个顶点一次且仅一次的圈为哈密顿圈。
  • 称穿过有向图 中每个顶点的基本回路为哈密顿回路。
  • 有哈密顿圈或哈密顿回路的图称为哈密顿图。

• 哈密顿链：称穿过无向图 中每个顶点的基本链（顶点不同的链）为哈密顿链。

• 哈密顿通路：称穿过有向图 中每个顶点的基本通路为哈密顿通路。

• 从哈密顿回路中去掉一条弧就成为哈密顿通路，从哈密顿圈中去掉一条边就成为哈密顿链。哈密顿回路是完备回路，哈密顿通路是完备通路，所以有向哈密顿图是强连通的，存在哈密顿通路的有向图是单向连通的。存在哈密顿链的无向图是连通的。

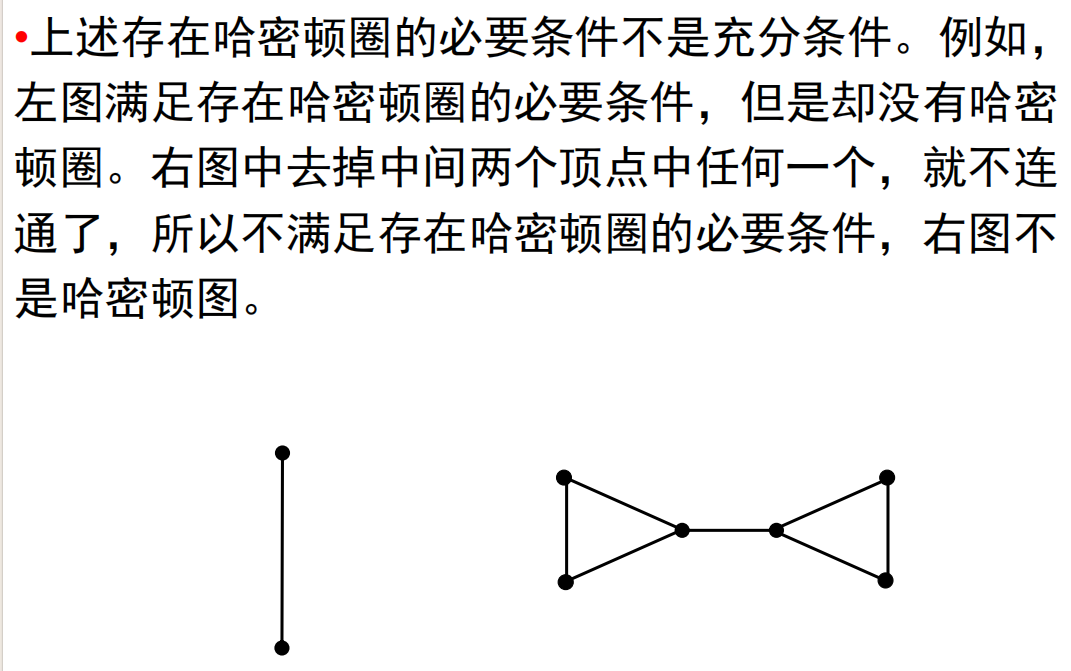
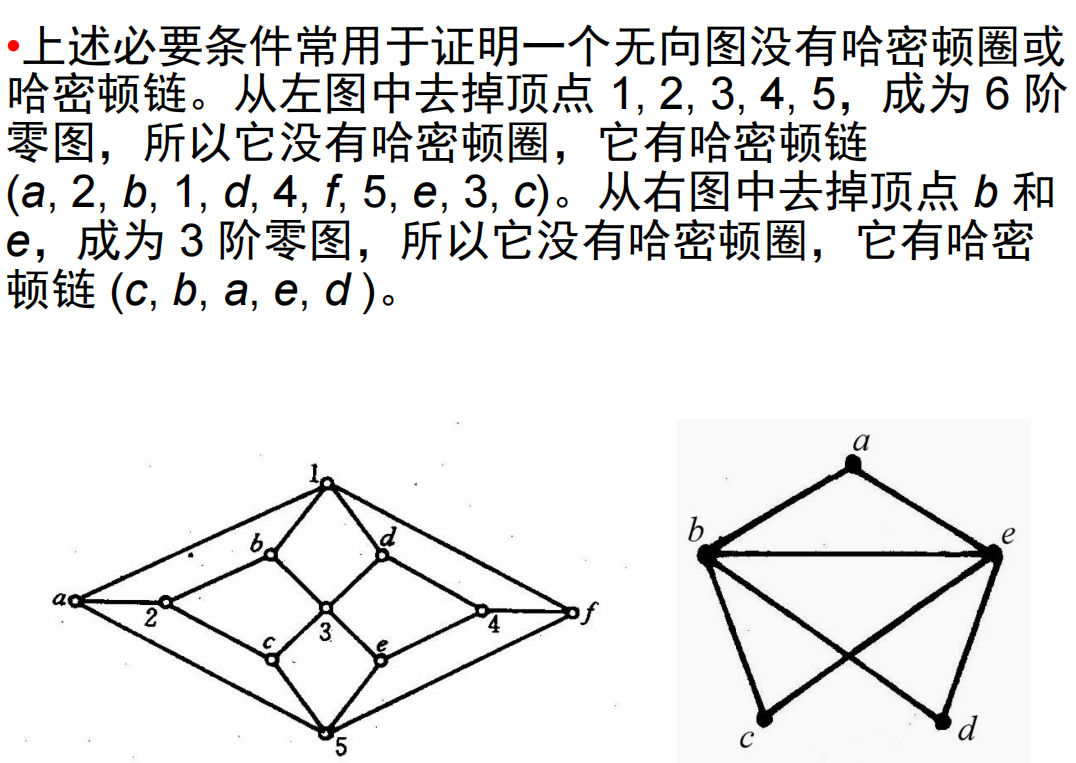
• 哈密顿图的必要条件（只能判断不是哈密顿图）：若无向图 ＝ 是哈密顿图， 是 的非空真子集，则 。其中 是从 中删除 中所有顶点及它们关联的边所得子图的连通分支数。
  

• 哈密顿链的必要条件（只能判断不是哈密顿链）：若无向图 ＝ 有哈密顿链， 是 的非空真子集，则 。其中 是从 中删除 中所有顶点及它们关联的边所得子图的连通分支数。
  

• 哈密顿链的充分条件：若 阶简单无向图 中每对不相邻顶点次数之和 ，则在 中存在哈密顿链。

• 哈密顿图的充分条件：设 ，若 阶简单无向图 中每对不相邻顶点次数之和 ，则 是哈密顿图。

• 定理13.4：在有向完全图中必存在哈密顿通路。

• 凡是强连通的有向完全图一定有哈密顿回路。

第14章 二分图的匹配问题

14.1 基本概念

• 二分图、互补顶点子集：设 是无向图。若可以将 分成两个非空子集 和 ，并且使得同一子集中的任何两个顶点都互不邻接，则称 为二分图。并称 和 为 的互补顶点子集。即二分图的每条边都连接着 中的一个顶点和 中的一个顶点。或者说任何一条边的两个端点，必然一个在 中，一个在 中。
  若非平凡图 的每个连通分支都是二分图或平凡图，则 是二分图。
  二分图中必没有三角形的圈。

• 完全二分图：设 和 是二分图 的互补顶点子集，若 中每个顶点都与 中每个顶点邻接，则称 为完全二分图。互补顶点子集分别有 个顶点和 个顶点的完全二分图记为 。
  左图是 ，右图是 。
  

• 若无向图 中有长度为奇数的闭合链，则在 中有长度为奇数的圈。

• 定理14.1：非平凡无向图 是二分图当且仅当 的每个圈的长度都是偶数。

判断是不是二分图：构造两个点的集合，证明二者互补

• 匹配（二分图左边的点和右边的点相连，每个点最多连一条线）：设 是二分图， 。若 中任何两条边都不相邻，则称 为 的匹配。
  中的边一定把 中的一些顶点和 中的相同数目的一些顶点一一配成对。
  中不一定把 中的顶点都包括了。

14.2 二分图的最大匹配

• 最大匹配：在二分图 的所有匹配中，边数最多的匹配称为最大匹配。
• 交错链：设 是二分图 的匹配， 是 中的基本链。若 中任何相邻的两条边中恰有一条属于 ，则称 为关于 的交错链，或简称为交错链。（即交错链中属于M的边和不属于M的边是交替出现的）
• 饱和顶点/非饱和顶点：设 是二分图 的匹配，称与 中的边关联的顶点为 的饱和顶点，称不与 中任何边关联的顶点为 的非饱和顶点。
• 可扩充链：两个端点都是匹配 的非饱和顶点的交错链称为关于 的可扩充链。
  可扩充链长度一定是奇数
  不在匹配中的边比在匹配中的边多一条
  可扩充链的两个非饱和端点，一定一个属于X，一个属于Y
  若将可扩充链中原来属于匹配的边从匹配中去掉，而将原来不属于匹配的边加入匹配中，则可得到多一条边的新匹配。
• 定理14.2：二分图 的匹配 是最大匹配当且仅当 中不存在关于 的可扩充链

14.3 从X到Y的匹配

• 从X到Y的匹配：设 和 是二分图 的互补顶点子集， 是 的匹配。若 中每个顶点都是 的饱和顶点，即是 中某条边的端点，则称 为从 到 的匹配。
  显然，若存在从 到 的匹配，则 。
  若 是从 到 的匹配，则 是最大匹配。

• 的邻域 ：设 ，所有与 中顶点相邻的顶点组成的集合称为 的邻域，记为 。显然， 。

• 定理14.3 从X到Y的匹配的充要条件：设 和 是二分图 的互补顶点子集。 中存在从 到 的匹配当且仅当满足以下相异性条件：对于 的任意子集 ，。

• 从X到Y的匹配的算法：

  1. 先任意找 中一个匹配 作为初始匹配.
  2. 如果 还不是从 到 的匹配, 即有 为非饱和顶点.
  3. 根据相异性条件, 设 有邻接顶点 :
     • 若有某个 为非饱和顶点, 则可扩充 进 ;
     • 若这 个邻接顶点都是饱和顶点,
       1. 则可构造 条以 为起点的交替链,
       2. 并基于相异性条件, 必可找到一条可扩充链.

• 定理14.4 t条件 从X到Y的匹配的充分条件：设 和 是二分图 的互补顶点子集。若存在正整数 ，使得 中每个顶点的次数 ，而 中每个顶点的次数 ，则 中存在从 到 的匹配。

判断二分图是否存在从 到 的条件

• 先用定理14.4
  • 成立：存在
  • 不成立：用定理14.3
    • 成立：存在
    • 不成立：不存在