11.1 邻接矩阵

11.1.1 有向图的邻接矩阵

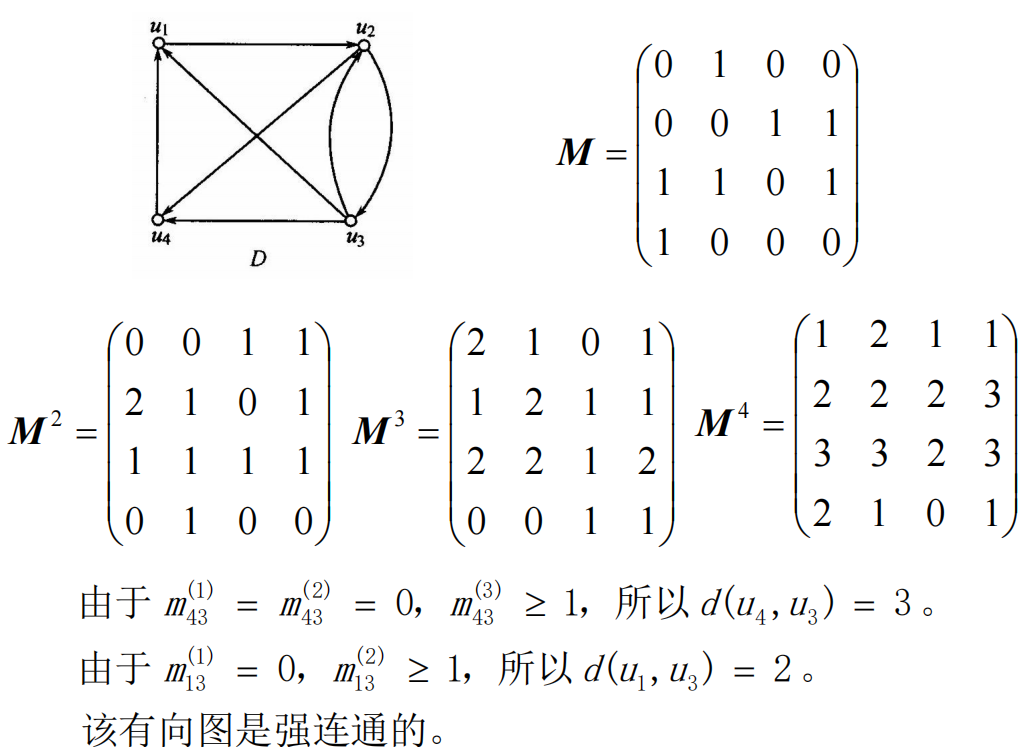
• 邻接矩阵：设简单有向图 ，， 的邻接矩阵 定义为

  若若

  邻接矩阵 M 即为 A 的关系矩阵。
  有向图 D1 和 D2同构当且仅当适当排列顶点的顺序可使它们的邻接矩阵相同。
  因为简单图没有自环，所以邻接矩阵 M 的主对角线全为 0。
  点的度数

• 邻接矩阵：可以将邻接矩阵的概念推广到有自环和平行弧的一般有向图。设 ，，有向图 的邻接矩阵 定义为 弧 的重数

• 定理11.1：设 是有向图，， 是 的邻接矩阵，，则 是从顶点 到顶点 的长度为 的通路的条数。

  • 等于顶点 上 长度为 的回路的条数。
  • 是 到 的最短通路的长度，所以其是使 中第 行第 列的元素有非零值的最小正整数
  • 对于 和 ＝，如果 中第 行第 列的元素均为0，又结合定理9.4（任何基本通路的长度不超过n-1），则可得从 到 不存在任何通路，因而属于不同的强分图。

11.1.2 无向图的邻接矩阵

• 邻接矩阵：设简单有向图 ，， 的邻接矩阵 定义为

  若若

  简单无向图G 的邻接矩阵M 是对称矩阵
  主对角线元素都是0
  点的度数

• 邻接矩阵：可以将邻接矩阵的概念推广到有自环和平行边的一般无向图。设，，无向图 的邻接矩阵 定义为 边的重数

• 定理11.2：设 是无向图，， 是 的邻接矩阵，，则 是从顶点 到顶点 的长度为 的链的条数。

11.2 有向图的可达性矩阵

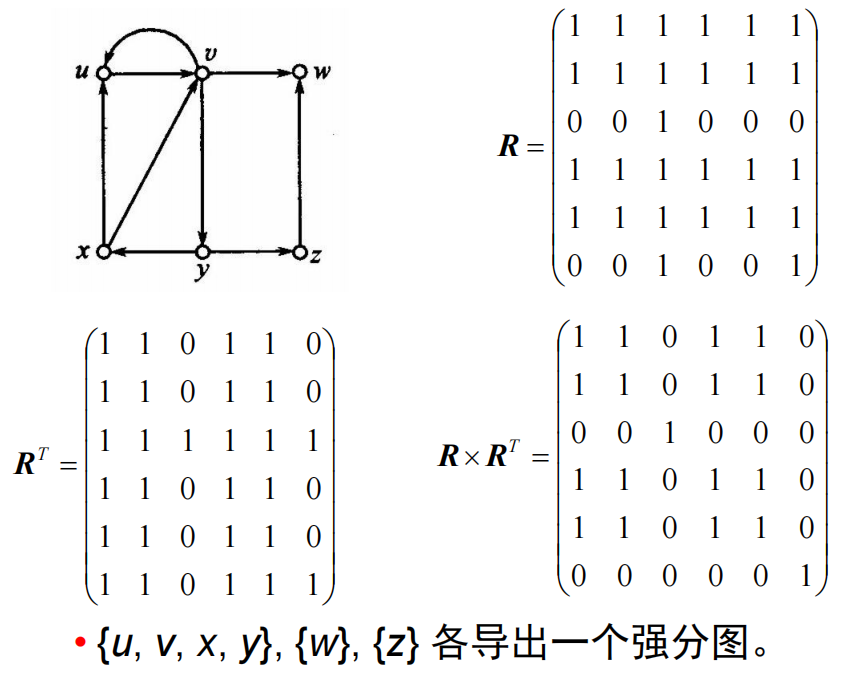
• 可达性矩阵：设有向图 ，， 的可达性矩阵 定义为

  若可达否则

  因为每个顶点可以到达自己，所以任何有向图的可达性矩阵的主对角线元素全为1

• 布尔函数：对于矩阵 ，定义 。 将矩阵 中的大于 1 的元素都改成1。

• 定理11.3：设 和 分别是 阶有向图 的可达性矩阵和邻接矩阵，则，其中 是 阶单位矩阵。

• 可达矩阵的应用：求包含指定顶点的强分图以及此强分图中所含顶点的数目。

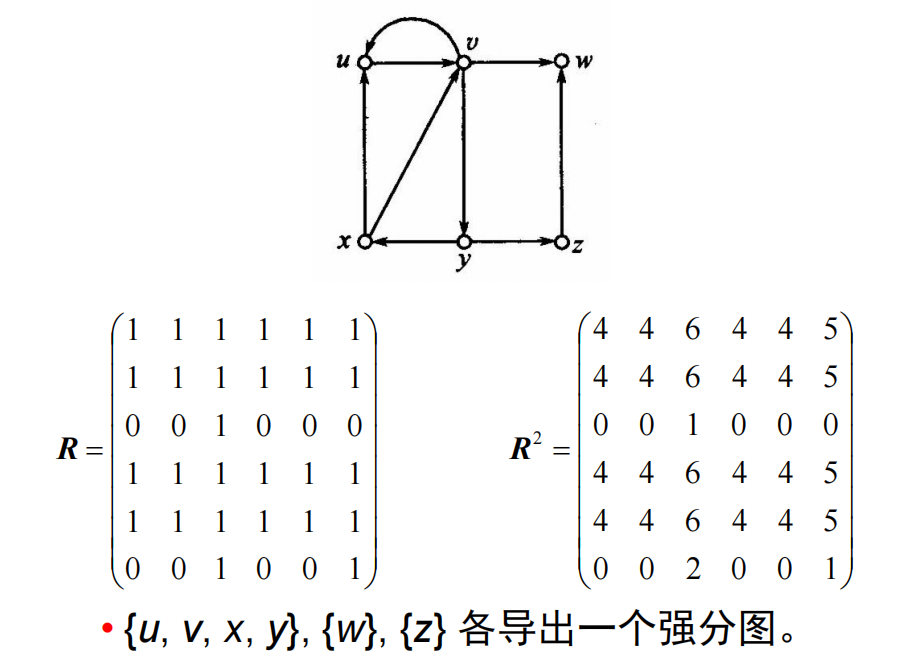
• 元素积：设 且 ，称 为 和 的元素积。

• 定理11.4：设 是有向图 的可达性矩阵，并设 ，则

  • 由 的第 i 行（列）中等于 1 的元素对应的顶点导出的子图是 所在的强分图。
    解释： 的 表示 i 可达 j， 的 表示 j 可达 i，故 中 的表示 i j 互达
  • ui所在的强分图有sii个顶点。
    与 互达的顶点数
    
    

• 设 R 和 M 分别是 n 阶有向图 D 的可达性矩阵和邻接矩阵，则

  • 是强连通的当且仅当 的元素全为 1。
  • 是单向连通的当且仅当 的元素全为 1。
  • 是弱连通的当且仅当 的元素全为 1，其中 。
  • 是无回路的当且仅当 的主对角线元素全为 0。

11.3 关联矩阵(Incidence Matrix)

11.3.1 有向图的关联矩阵

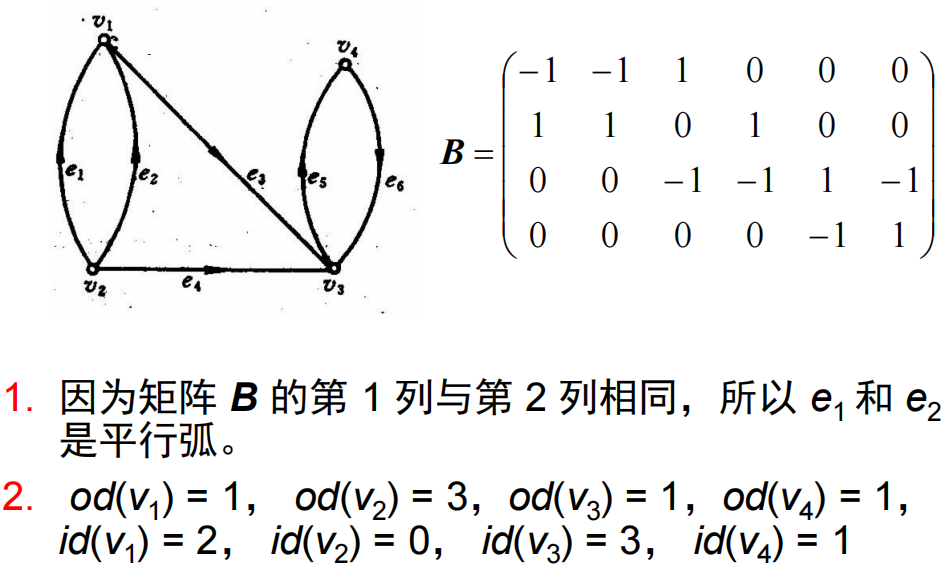
• 关联矩阵：设无自环有向图 不是零图，其中 ，， 的关联矩阵 定义为
  若是弧的始点若是弧的终点若不是弧的端点
  矩阵 每列元素之和都是0。
  若 的第 i 列与第 j 列相同，则 和 是平行弧。
  的第 i 行中 1 的个数 = 顶点 的出度，
  的第i行中 −1 的个数 = 顶点 的入度。
  

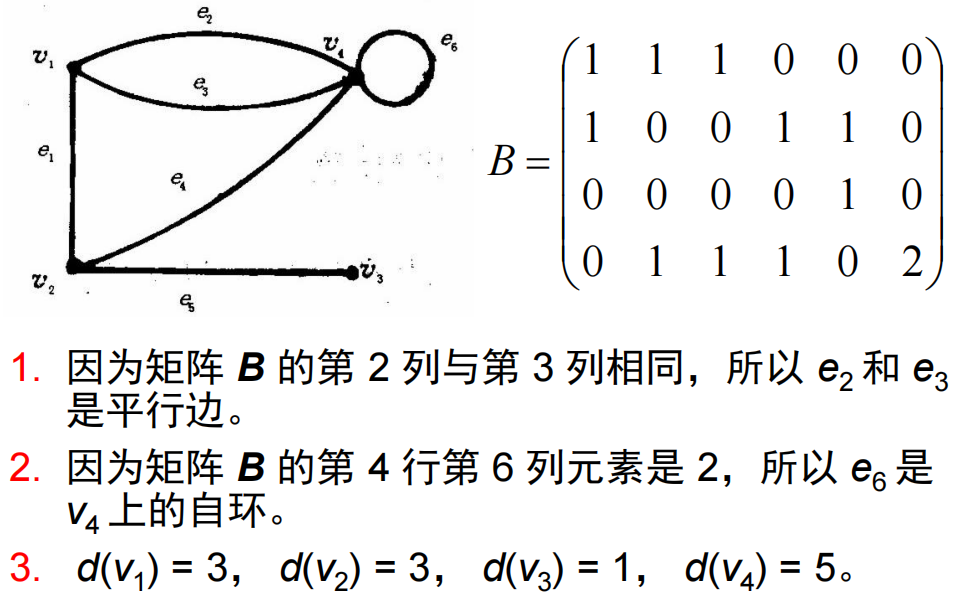
11.3.2 无向图的关联矩阵

• 关联矩阵：设无自环有向图 不是零图，其中 ，， 的关联矩阵 定义为
  与的关联次数
  矩阵 每列元素之和都是 2
  若 的第 i 行第 j 列是 2，则 是 上的自环
  若 的第 i 列与第 j 列相同，则 和 是平行弧
  的第 i 行元素之和 = 顶点 的度