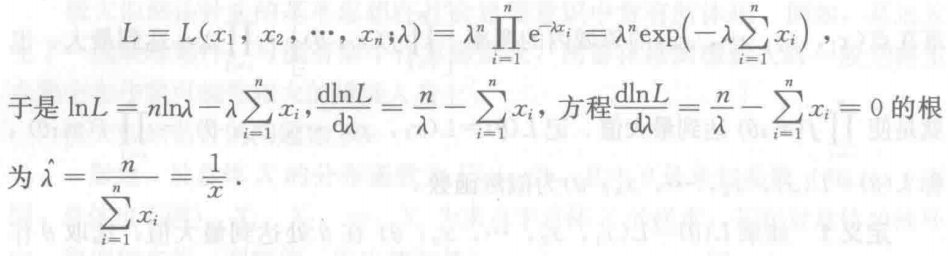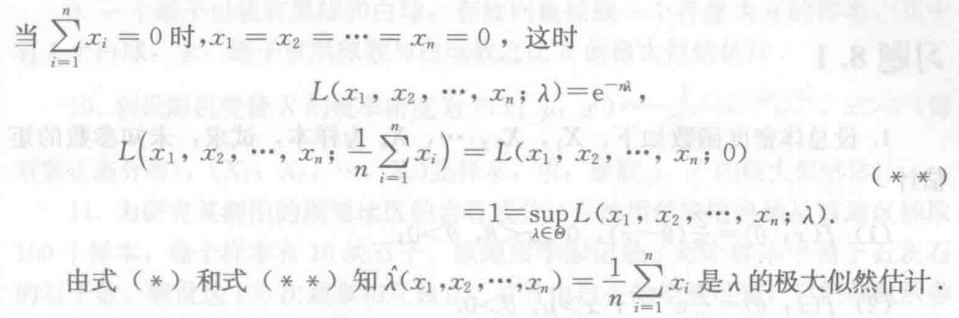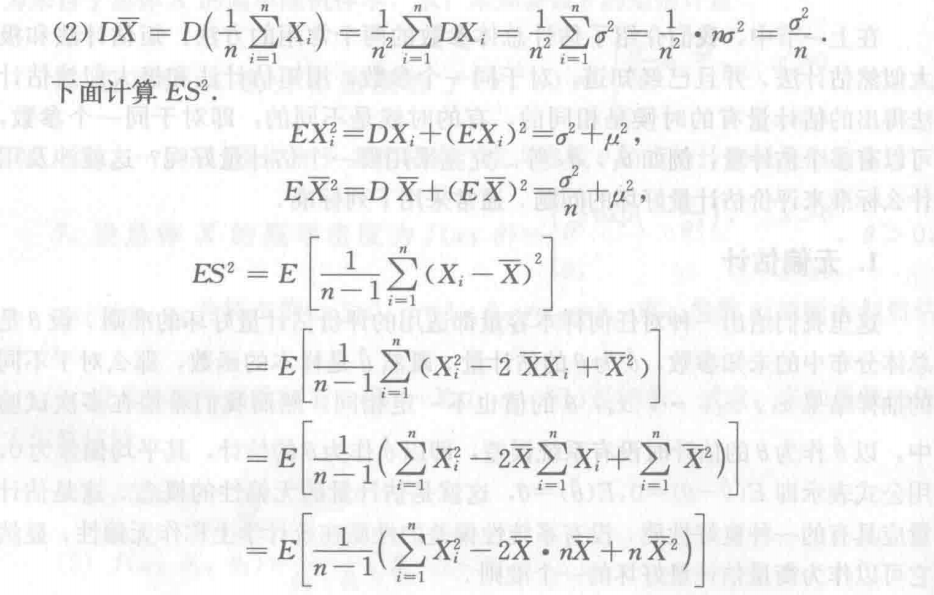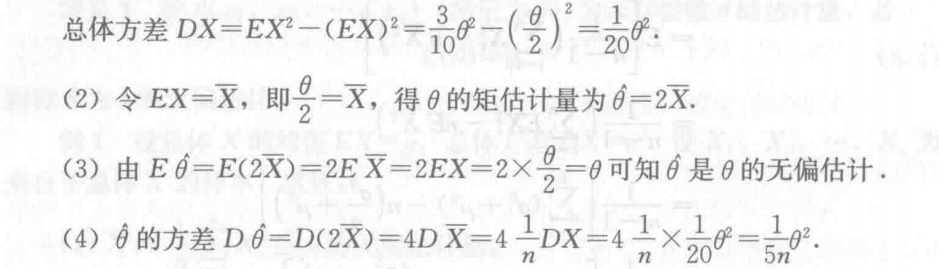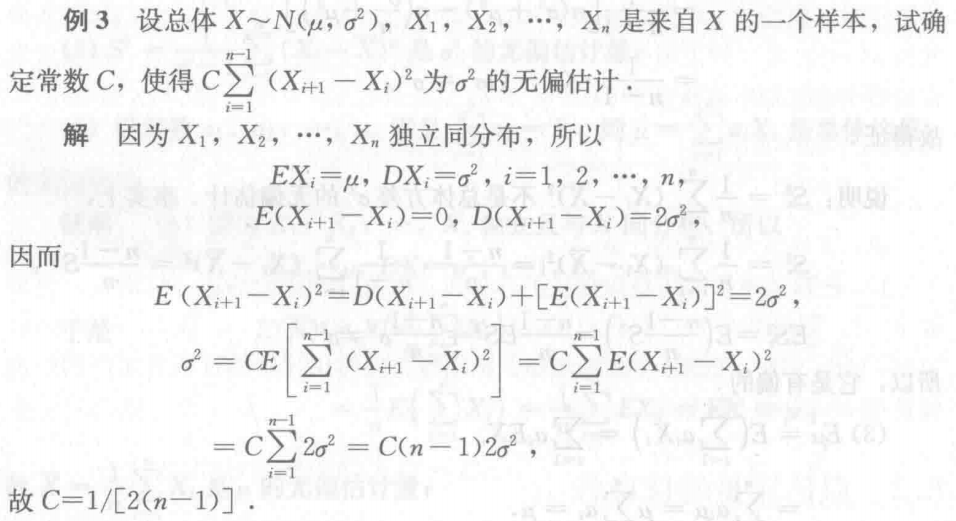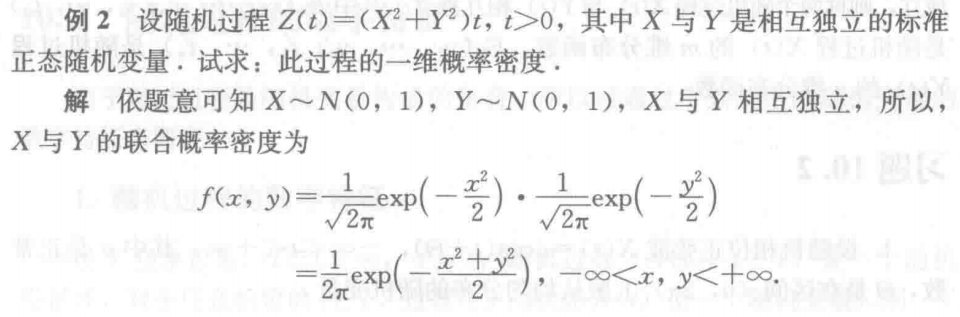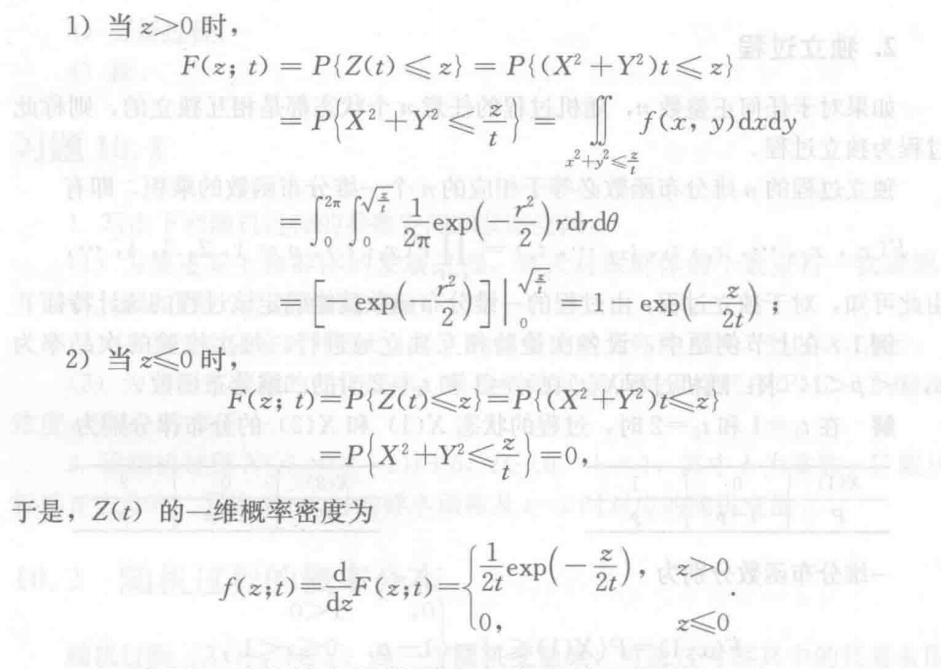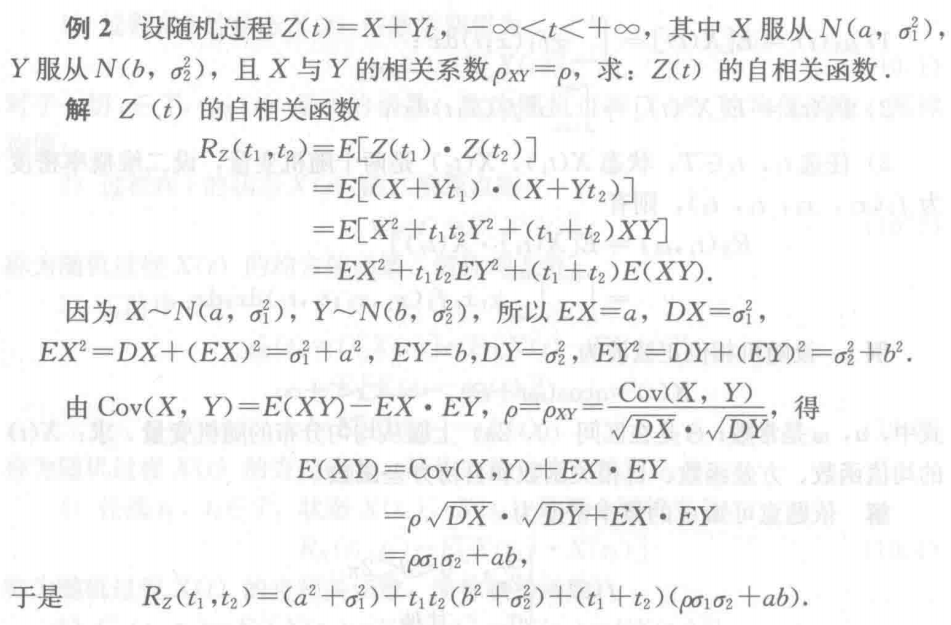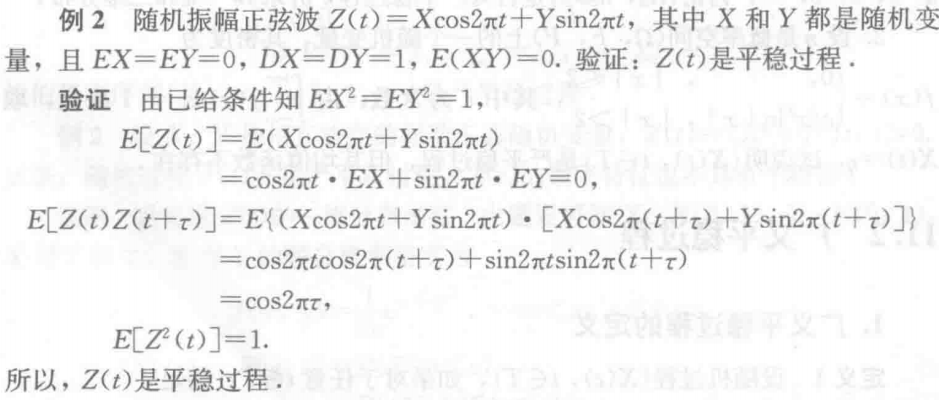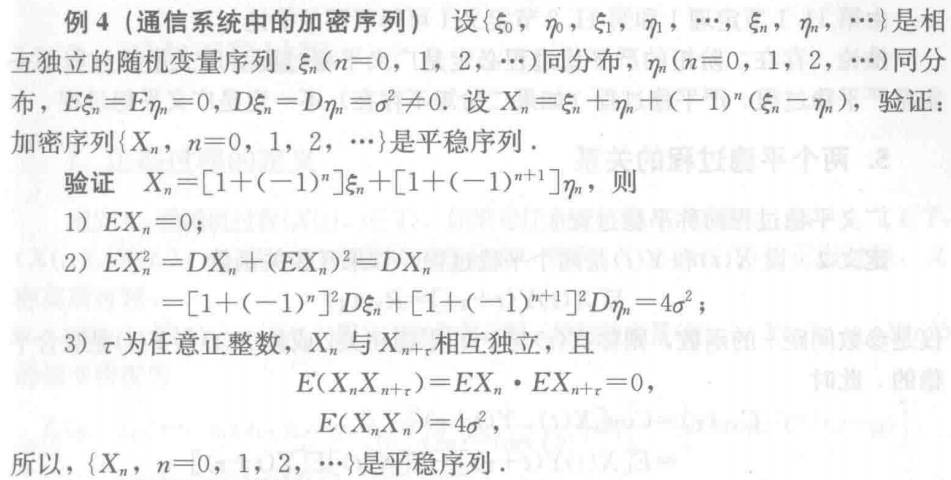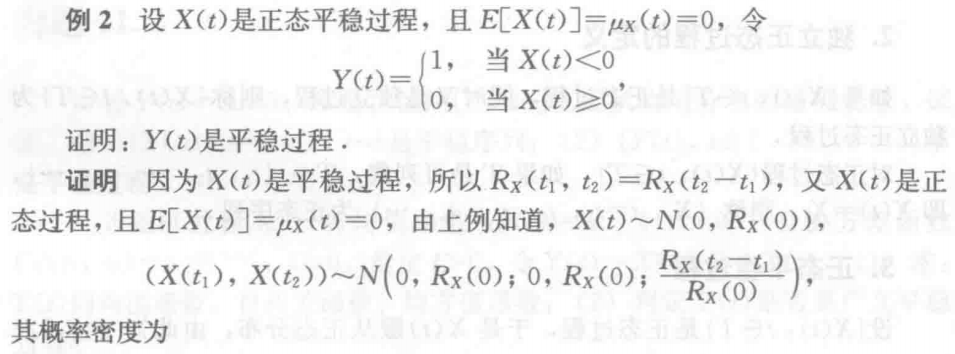04

8 参数估计

8.1 参数的点估计

8.1.1 矩估计法

用样本矩估计相应的总体（随机变量）矩。
只要总体的 阶矩存在，样本 阶矩依概率收敛于相应的总体 阶矩。

具体过程

设总体 的分布函数为 ，未知参数为 .

  1. 求出总体矩： 或
  2. 对总体进行随机抽样，设 为来自于总体 的样本， 为样本值；
  3. 构造样本矩：；
  4. 由于：；
  5. 联立并解方程组求出 .

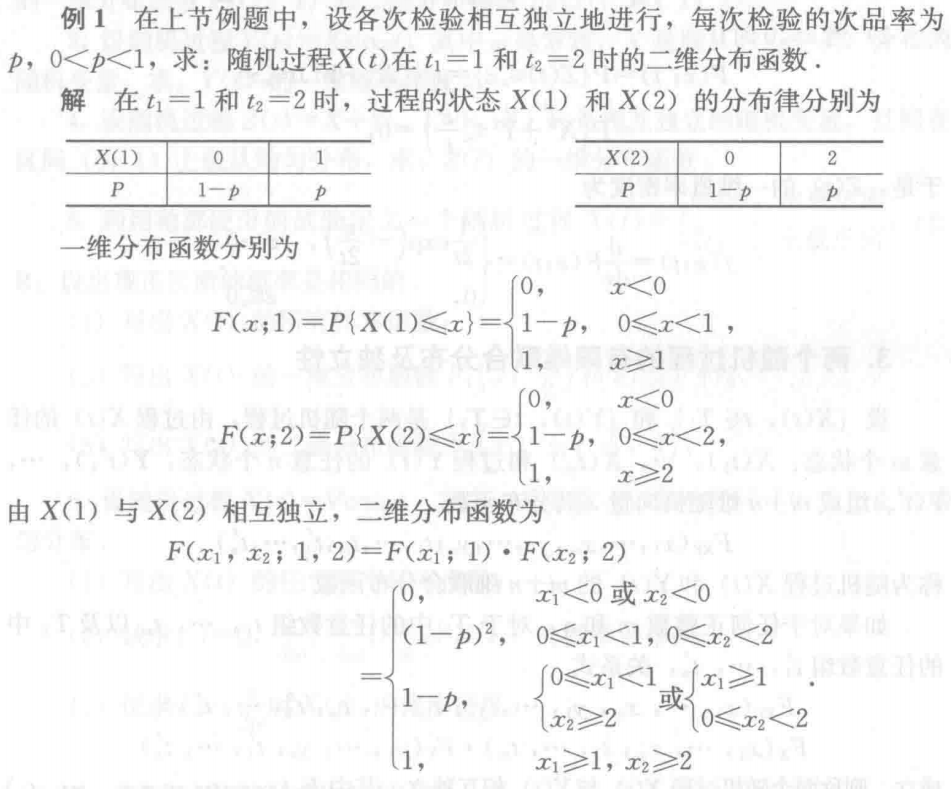
例1

Pasted image 20241120103007.png

例2

Pasted image 20241120103036.png

8.1.2 极大似然估计法

根据样本的具体情况，选择总体参数的估计，使得该样本发生的概率最大。

1 连续情形

定义

若 是连续型随机变量，概率密度函为 ，其中 为未知参数， 落在点 邻域内的概率为
选取总体参数 的估计值 ，使得此概率达到最大，即 达到最大值。
称为极大似然函数。

单参数解法
  1. 求
  2. 解方程 或
多参数解法
  1. 求
  2. 解方程
例

Pasted image 20241120105448.png
Pasted image 20241120105503.png
Pasted image 20241120105534.png
Pasted image 20241120105745.png
Pasted image 20241120105809.png

2 离散情形

定义

若 是离散型随机变量，分布律 形式已知，参数 未知， 为样本 的样本观察值。
取到 的概率：

选取总体参数 的估计值 ，使得此概率达到最大，即 达到最大值。
称为极大似然函数。

解法

同上

例1

Pasted image 20241120110224.png
Pasted image 20241120110243.png

例2

Pasted image 20241120110529.png

8.2 点估计的优良性

8.2.1 无偏估计

定义

设 （简记为 ）为未知参数 的估计量，若 （真值），则称 为 的无偏估计。

例1

Pasted image 20241120112404.png
Pasted image 20241120112428.png
Pasted image 20241120112453.png

例2

Pasted image 20241120112514.png
Pasted image 20241120112527.png

例3

Pasted image 20241120112545.png

8.2.2 最小方差无偏估计

定义

设 是 的一个无偏估计，若对于 的任一无偏估计 ，成立：

则称 是 的最小方差无偏估计。
若 和 都是无偏估计量，且 ，则称估计量 较 有效，或较佳，或较优。

例1

Pasted image 20241120113249.png

例2

Pasted image 20241120113314.png
Pasted image 20241120113326.png

8.2.3 一致估计

定义

设 为未知参数 的估计量，若 依概率收敛于 ，即对任意的 ，则称 为 的一致性估计。

例1

Pasted image 20241120115600.png

例2

Pasted image 20241120115615.png

8.3 区间估计与置信区间

8.3.1 置信区间

设总体分布含有一未知参数 ，又 为来自于总体的样本，若对给定的 ，统计量 和 满足：

则称区间 为 相应于置信度是 的置信区间，简称置信区间。

分别称为置信下限和置信上限。

注

  1. 统计量 和 是随机变量，区间 是置信区间。

对于 ，区间 是普通区间。

  1. 较小时，随机区间以较大的概率包含

  2. 置信区间的长度意味着误差，因此越小越好

8.3.2 单侧置信限

若对于给定的 ，统计量 满足 ，则称区间 为 相应于置信度是 的单侧置信区间，称 为置信度为 的单侧置信下限。

若对于给定的 ，统计量 满足 ，则称区间 为 相应于置信度为 的单侧置信区间，称 为置信度为 的单侧置信上限。

8.4 正态分布均值和方差的区间估计

8.4.1 均值 的区间估计

1.方差 已知，对 进行区间估计

设总体 ，其中 已知，又 为来自于总体的样本。

求出统计量 使：

区间 为 的置信度为 的置信区间

  • 特别的，对于不服从正态分布的总体，只要n足够大，则由中心极限定理，随机变量 近似地服从标准正态分布，因此仍然有 作为 的置信区间
证明

Pasted image 20241127102109.png
Pasted image 20241127102122.png

例

Pasted image 20241127102241.png

注：标准正态分布 的 分位点
定义

设 是一个标准正态随机变量，给定 ，若存在唯一的 ，使得：

称 为标准正态分布的 分位点（或 分位数），简称分位点。

分位点的性质：

有：

  1. 或
  2. 或
  3. 或

对于给定的 ，标准正态分布的双侧分位点 ，使：

即：

2.方差 未知，对 进行区间估计

设 为正态总体 的一个样本，由于 未知，用样本方差 来代替总体方差
故均值 的置信区间为
其中

证明

Pasted image 20241127102836.png

例1

Pasted image 20241127103006.png
Pasted image 20241127103017.png

例2

Pasted image 20241127103047.png

例3

Pasted image 20241127103105.png
Pasted image 20241127103118.png

8.4.2 方差 的区间估计（总体均值未知）

设总体 是总体的样本，当总体 的参数 未知时，
方差 的置信区间为
的置信区间是

注

选取的临界值 不是唯一的。

证明

Pasted image 20241127103337.png
Pasted image 20241127103348.png

例

Pasted image 20241127103417.png

9 假设检验

9.1 假设检验的概念

先对总体的参数或总体的分布形式作某种假设 ，然后由抽样结果推断假设 是否成立。

在数理统计学中，称检验假设 的方法为假设检验。

  • 参数的假设检验
  • 分布的假设检验
检验假设的理论依据

小概率事件在一次试验（抽样）中是不可能发生的

假设检验的一般步骤

Pasted image 20241127112114.png

9.2 正态总体均值和方差的假设检验

假设检验过程中的两类判断错误（判断失误）

  1. 当判断 伪（拒绝 ）时，实际情况 真——此为第一类错误（弃真）（概率小于或等于 ）
  2. 当判断 真（接受 ）时，实际情况 伪——此为第二类错误（纳伪）（概率为 ）

当样本容量 固定时，犯两类错误的概率大小时相互制约的，即减小其中一个，另一个往往会增大。

通常的实际做法是：设置检验水平 来限制第一类错误（根据具体情况），再尽量减小第二类错误。（增大样本容量 ）

在实际问题中，如何给定检验水平 ，应根据具体情况而定

  1. 当拒绝一个属真的假设，即犯第一类错误后果非常严重时，应将 取得小一些，如 等；
  2. 当取伪会引起严重后果时，可将 取得适当大一些，如 等。

9.2.1 已知

1. 已知，检验假设

由样本提供的信息计算 的值，查 表得

  • 若 则拒绝原假设 （ 伪），接受 ；
  • 若 则接受原假设 （ 伪）。
具体步骤
  1. 提出假设：
    原假设备选假设
  2. 在 为真时，构建检验统计量
  3. 确定检验水平 和拒绝域
    对于给定的检验水平 ，
    则 ，即 是小概率事件，从而，拒绝域：
  4. 由样本提供的信息计算 的值，查 表得
    • 若 则拒绝原假设 （ 伪），接受 ；
    • 若 则接受原假设 （ 伪）。
  5. 得出结论
例

Pasted image 20241127141159.png
Pasted image 20241127141214.png

2. 已知，检验假设

由样本提供的信息计算出

  • 若 则拒绝原假设（ 伪），接受 ；
  • 若 则接受原假设（ 真）
具体步骤

此时样本信息显示

  1. 提出假设
    原假设备选假设
  2. 构建检验统计量
  3. 确定拒绝域
  4. 由样本提供的信息计算出
    • 若 则拒绝原假设（ 伪），接受 ；
    • 若 则接受原假设（ 真）
  5. 给出结论
例

Pasted image 20241127141308.png

3. 已知，检验假设

由样本提供的信息计算出

  • 若 则拒绝原假设（ 伪），接受 ；
  • 若 则接受原假设（ 真）
具体步骤

此时样本信息显示

  1. 提出假设
    原假设备选假设
  2. 构建检验统计量
  3. 确定拒绝域
  4. 由样本提供的信息计算出
    • 若 则拒绝原假设（ 伪），接受 ；
    • 若 则接受原假设（ 真）
  5. 得出结论
例

Pasted image 20241127141354.png
Pasted image 20241127141409.png

9.2.2 未知

1. 未知，检验假设

由样本计算出 ，然后与 进行比较

  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
具体步骤

由于 未知，这时 已不是统计量，因此我们用 的无偏估计量 来代替

  1. 提出假设
    原假设备选假设
  2. 构建检验统计量
  3. 确定拒绝域
    从而，拒绝域
  4. 由样本计算出 ，然后与 进行比较
  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
  1. 得出结论
例1

Pasted image 20241127141602.png
Pasted image 20241127141614.png

例2

Pasted image 20241127141638.png

2. 未知，检验假设

由样本计算出 ，然后与 ​ 进行比较

  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
具体步骤

事先计算出样本值

  1. 提出假设
    原假设备选假设
  2. 构建检验统计量
  3. 确定拒绝域
    从而，拒绝域
  4. 由样本计算出 ，然后与 ​ 进行比较
  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
  1. 得出结论

3. 未知，检验假设

  1. 由样本计算出 ，然后与 ​ 进行比较
  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
具体步骤

事先计算出样本值

  1. 提出假设
    原假设备选假设
  2. 构建检验统计量
  1. 确定拒绝域

从而，拒绝域
4. 由样本计算出 ，然后与 ​ 进行比较

  • 若 ，则拒绝假设 ，接受
  • 若 ，则接受假设
  1. 得出结论

以上三种检验法均采用了 分布，故又名 检验法。

9.2.3 正态总体方差的假设检验

1. 检验假设

根据样本值计算

  • 若 或 则拒绝假设 ，接受
  • 否则接受假设
具体步骤
  1. 提出假设
  2. 构建检验统计量
  1. 确定拒绝域

从而拒绝域
4. 根据样本值计算

  • 若 或 则拒绝假设 ，接受
  • 否则接受假设
  1. 得出结论
例1

Pasted image 20241127142205.png
Pasted image 20241127142215.png

例2

Pasted image 20241127142540.png

2. 检验假设

根据样本值计算

  • 若 则拒绝假设 ，接受
  • 否则接受假设
具体步骤
  1. 提出假设
  2. 构建检验统计量
  3. 确定拒绝域
    从而拒绝域
  4. 根据样本值计算
  • 若 则拒绝假设 ，接受
  • 否则接受假设
  1. 得出结论

3. 检验假设

根据样本值计算

  • 若 则拒绝假设 ，接受
  • 否则接受假设
例

Pasted image 20241127142624.png

具体步骤
  1. 提出假设
  2. 构建检验统计量
  3. 确定拒绝域
    从而拒绝域
  4. 根据样本值计算
  • 若 则拒绝假设 ，接受
  • 否则接受假设
  1. 得出结论

注：假设检验与置信区间的关系

假设 的检验实质上是找出 的置信区间，如果 落在置信区间内，则接受原假设 ；如果落在置信区间外，就拒绝假设

10 随机过程的基本概念

10.1 随机过程的定义及分类

10.1.1 随机过程的定义

定义1

给定参数集 ，对于固定 ，对应有随机变量 ，对应所有 ，是一族随机变量 ，则称随机变量族 为随机过程。

对任意给定的 是一个随机变量，称为随机过程在 时的状态变量，简称状态。

定义2

设随机试验 的样本空间 ， 是非空集合，若对于固定 ，对应关于参数 的函数 称为随机过程的样本函数（或随机过程的一个实现，也称为一条轨道）。

对于所有的 ，得到一族 的函数 ，称为随机过程，简称过程。简记为 或 .

称为参数集。

由定义2得
  • 对于 中的每一个 ， 是仅依赖于 的函数，称为随机过程的样本函数，它是随机过程的一次物理实验或对应于 的轨道
  • 对任意给定的 ， 是一个随机变量，称其为随机过程在 时的状态变量，简称状态
定义3

定义在 上的二元函数 ，对于每个固定的 ， 是可测函数，则称 为随机过程。

对于固定的 ， 是随机变量，其所有可能的取值构成的实数空间，称为随机过程的状态空间。它是二元函数 的值域，记为 。

例

Pasted image 20241204095825.png

10.1.2 随机过程的分类

1. 按随机过程的参数集和状态空间分类

  • 参数集 可能为离散集或连续集
  • 状态空间 可能为离散集或连续集
  1. 离散， 离散（贝努里随机过程）
  2. 离散， 连续

参数离散随机过程是随机变量序列，简称随机序列。

一般地记 ，于是

  1. 连续， 离散（泊松过程）
  2. 连续， 连续

2. 按随机过程的概率结构分类

  • 二阶矩过程，包括正态过程，平稳过程等
  • 马尔可夫过程
    • 马尔科夫链
    • 泊松过程
    • 维纳过程
    • 扩散过程
  • 更新过程
  • 鞅

10.2 随机过程的概率分布

10.2.1 随机过程的n维分布函数

设 是一随机过程，对于参数集 中的任意 个元素： 相应有过程分别在 的 个状态：

个状态（随机变量）的联合分布函数

称为随机过程 的 维分布函数。

如果存在非负函数 ，使得：

成立，则称 为随机过程 的 维概率密度，

10.2.2 独立过程

如果对于任何正整数 ，随机过程的任意 个状态都是相互独立的，则称此过程为独立过程。
独立过程的 维分布函数（或 维概率密度）必等于相应的 个一维分布函数（一维概率密度）的乘积，即有：

例

Pasted image 20241204101141.png
Pasted image 20241204101248.png
Pasted image 20241204101256.png

10.2.3 两个随机过程的有限维联合分布及独立性

设 和 是两个随机过程，由 的任意 个状态 和 的任意 个状态 组成 维随机向量。其分布函数：

称为随机过程 和 的 维联合分布函数。

如果对于任何正整数 和 ，对于 和 中的任意数组，关系式：

都成立，则称两个随机过程相互独立。

10.3 随机过程的数字特征

10.3.1 随机过程的数字特征

参数集 ，随机变量族 是一个随机过程，对于任意给定 , 过程在 的状态 是随机变量，一维概率密度 。

  1. 过程在 的状态 的数学期望

    对于一切 ， 是 的函数，称为随机过程 的均值函数，简称均值。

  2. 过程在 的状态 的二阶原点矩

    称为随机过程 的均方值函数，简称均方值

  3. 过程在 的状态 的二阶中心矩

    称为随机过程 的方差函数，简称方差。标准差/均方差函数

  4. 任选 ，状态 是两个随机变量

    称为随机过程 的自相关函数，简称相关函数

  5. 称为随机过程 的自协方差函数，简称协方差函数

  • 均值、均方值、方差是刻画随即过程在各个状态的统计特性
  • 相关函数和协方差函数是刻画随机过程的任何两个不同状态的统计特性
数字特征间的关系

10.3.2 连续型随机过程的数字特征

对连续型随机过程 ，设一维概率密度为 ，则有

任选 ，状态 是两个随机变量，二维概率密度 ，则有

例1

Pasted image 20241204112751.png

例2

Pasted image 20241204112903.png

10.3.3 两个随机过程的互相关函数

两个随机过程 和 ，任选 ，对应有过程 在 的状态 ，过程 在 的状态 。

  1. 和 的二阶原点混合矩

    称为随机过程 和 的互相关函数

  2. 和 的二阶中心混合矩

    称为随机过程 和 的互协方差函数
    且有

  3. 如果对任意 ，都有 ，亦即 ，则称随机过程 和 是不相关的。
    显然，两个相互独立的随机过程必不相关

例

Pasted image 20241204113507.png
Pasted image 20241204113516.png

11 平稳过程

11.1 严平稳过程

11.1.1 严平稳过程的定义

对于任意实数 ，如果随机过程 的任意 维分布满足：

（严平稳条件）

则 称为严，强或狭义平稳过程。

若参数 表示“时间”，则严平稳过程的任何有限维概率分布不随时间的平移而变化。

11.1.2 严平稳过程的性质

  1. 状态离散的随机过程 的严平稳条件
  2. 状态连续的随机过程 的严平稳条件
  3. 特殊地，取
    • 一维分布函数
    • 二维分布函数
  • 一维分布函数 ：不依赖于参数
  • 二维分布函数 ：仅依赖于参数间距 ，而与 本身无关

11.1.3 严平稳过程的数字特征

定理

设 是严平稳过程，如果过程的二阶矩存在，那么

  • 均为常数，与参数 无关；
  • 仅依赖于
注：

这一性质也称为数字特征的平稳性

例

Pasted image 20241211100025.png
Pasted image 20241211100039.png
Pasted image 20241211100059.png

11.2 宽（广义）平稳过程

11.2.1 宽平稳过程的定义

设随机过程 ，对于任意 ，满足：

  2. 是常数
  3. 仅依赖于 ，而与 无关

则称 为宽，弱或广义平稳过程，简称平稳过程。

参数集 为可列集的平稳过程，又称为平稳序列，或称平稳时间序列。

11.2.2 平稳过程的例子

例1 证明是平稳过程

Pasted image 20241211101920.png

例2 证明是平稳过程

Pasted image 20241211101941.png

例3 证明是平稳序列

Pasted image 20241211102006.png
Pasted image 20241211102015.png

例4 证明是平稳序列

Pasted image 20241211102036.png

例5 证明是平稳过程

Pasted image 20241211102056.png
Pasted image 20241211102111.png

11.2.3 严平稳过程与宽平稳过程的关系

  1. 宽平稳过程不一定是严平稳过程
  2. 严平稳过程不一定是宽平稳过程
    • 存在二阶矩的严平稳过程必定是宽平稳过程

二阶矩 存在的随机过程称为二阶矩过程。

11.2.4 两个平稳过程的关系：平稳相关

设 和 是两个平稳过程，如果互相关函数 仅是参数间距 的函数，则称 和 平稳相关，或称它们是联合平稳的。此时：

定义：

称为标准互协方差函数。

11.3 正态平稳过程

11.3.1 正态过程的概念

1. 正态随机变量的有关知识

一维正态随机变量 的概率密度

二维正态随机变量 的概率密度

维正态随机变量 的概率密度

其中：

协方差矩阵

2. 正态过程的定义

如果随机过程 ，对任意正整数 ，， 服从正态分布，则称 为 正态过程，又称高斯(Gauss)过程。

设 为正态过程，则：

3. 独立正态过程的定义

如果 是正态过程，同时又是独立过程，则称 为独立正态过程。

正态过程 ，如果 是可列集，，记 ，那么 是正态序列。

4. 正态过程是二阶矩过程

设 是正态过程， 服从正态分布，则：

必存在，即二阶矩存在。

11.3.2 正态平稳过程

1. 定义

如果正态过程 又是广义平稳过程，则称 为正态平稳过程。

2. 定理

设 是正态过程，则 为严平稳过程 宽平稳过程。

3. 例题

例1 正态平稳过程的一维、二维服从的分布

Pasted image 20241211110645.png

例2 证明平稳过程

Pasted image 20241211110725.png
Pasted image 20241211110743.png

11.4 遍历过程（经历过程）

11.4.1 时间均值和时间相关函数

设随机过程
固定 ，样本函数 ， 在区间 上的函数平均值定义为：

在 上的函数平均值定义为：

当变化时，

\overline{x(t)} = \overline{X(e,t)} = \lim\limits{l \to +\infty}
\dfrac{1}{2l}\int^l{-l}X(e, t),dt

是随机过程对于参数的平均值，称为随机过程的时间均值。，有：

\begin{aligned}
\overline{X(t)X(t + \tau)}
= & \overline{X(e, t)X(e, t + \tau)}\
= & \lim\limits{l \to +\infty}
\dfrac{1}{2l}
\int^l{-l}
X(e, t)X(e, t + \tau),dt
\end{aligned}

称为随机过程的时间相关函数。随机过程

\begin{aligned}
&\overline{X(t)} = \lim\limits{l \to +\infty}
\dfrac{1}{l}
\int_0^l X(e, t), dt\
&\overline{X(t)X(t + \tau)} = \lim\limits{l \to +\infty}
\dfrac{1}{l}
\int_0^l X(e, t)X(e, t + \tau), dt
\end{aligned}

### 11.4.2 各态遍历性 设 $X(t)$ 是一个平稳过程，$T=(-\infty, +\infty)$ 或 $T=[0, +\infty)$ 1. 如果 $P\{\overline{X(t)} = E[X(t)] = \mu_X\} = 1$ ，则称过程 $X(t)$ 的**均值**具有**各态遍历性**； 2. 如果 $P\{\overline{X(t)X(t + \tau)} = E[X(t)X(t + \tau)] = R_X(\tau)\} = 1$ ，则称过程 $X(t)$ 的**自相关函数**具有**各态遍历性**。 **均值和自相关函数**都具有**各态遍历性**的平稳过程称为**遍历过程**，或者说，该过程**具有遍历性**。 #### 平稳过程均值各态遍历性的判别定理 ##### 均方连续 设随机过程 $\{ X(t),t\in T\}$ ，如果对于任意 $t\in T$ ，$E[X^{2}(t)]$ 存在且有限，则称 $\{X(t),t\in T\}$ 为**二阶矩过程**。 设 $\{ X(t),t\in T\}$ 为二阶矩过程，则 1. 对 $t_{0}\in T$ ，如果 $lim_{t\rightarrow t_{0}}E|X(t)-X(t_{0})|^{2}=0$ ，则称 $X(t)$ 在 $t_{0}\in T$ 处**均方连续**； 2. 若 $X(t)$ 在每一个 $t_{0}\in T$ 处都均方连续，则称 $\{X(t),t\in T\}$ 是**均方连续的**。 ##### 定理1 均值各态遍历性判别定理 平稳过程 $\{X(t), -\infty<t<+\infty\}$ 是一均方连续的平稳过程，则时间均值具有各态遍历性的充要条件是

\lim\limits_{l \to +\infty}
\dfrac{1}{l} \int_0^{2l}
(1 - \dfrac{\tau}{2l})[R_X(\tau) - \mu^2_X],d\tau = 0

##### 定理2 设 $\{X(t), t\in T = [0,+\infty)\}$ 是一均方连续的平稳过程，则时间均值具有各态遍历性的充要条件是

\lim\limits_{l \to +\infty}
\dfrac{1}{l} \int_0^{l}
(1 - \dfrac{\tau}{l})[R_X(\tau) - \mu^2_X],d\tau = 0

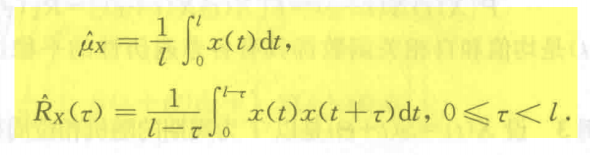### 11.4.3 遍历过程的数字特征 Pasted image 20241211145336.png|325 # 12 马尔可夫链 ## 12.1 马尔可夫链的定义 ### 12.1.1 定义 设随机过程 $\{X(t), t \in T\}$ 的状态空间 $S$ 是有限集或可列集，对任意正整数 $n$，对于 $T$ 内任意 $n+1$ 个状态参数 $t_1<t_2<...<t_n<t_{n+1}$ 和 $S$ 内任意 $n+1$ 个状态 $j_1, j_2, ..., j_n, j_{n+1}$，如果条件概率

\begin{aligned}
&P{X(t{n+1}) = j{n+1}|X(t1)=j_1, X(t_2)=j_2,...,X(t_n)=j_n}\
=&P{X(t{n+1})=j_{n+1}|X(t_n)=j_n}
\end{aligned}

恒成立，则称此过程为**马尔可夫链**。称式子所反映出的性质是**马尔科夫性**，或称**无后效性**。 ### 12.1.2 马尔可夫链的分类 状态空间 $S$ 是离散的（有限集或可列集），参数集 $T$ 可为离散或连续。 ### 12.1.3 离散参数马尔可夫链的转移概率 #### 1. 转移概率的定义 设离散参数马尔可夫链 $\{X(t), t = t_0, t_1, t_2, ..., t_n, ...\}$ 条件概率 $P\{X(t_{m+1})=j|X(t_m)=i\}=p_{ij}(t_m)$ 称为 $X(t)$ 在时刻（参数）$t_m$ 由状态 $i$ 一步转移到状态 $j$ 的**一步转移概率**，简称**转移概率**。 条件概率 $P\{X(t_{m+n})=j|X(t_m)=i\}=p_{ij}^{(n)}(t_m)$ 称为 $X(t)$ 在时刻（参数）$t_m$ 由状态 $i$ $n$ 步转移到状态 $j$ 的 **$n$ 步转移概率**。 #### 2. 转移概率的性质 对于状态空间 $S$ 内的任意两个状态 $i$ 和 $j$，恒有 1. $p_{ij}^{(n)}(t_m)\geq 0$ 2. $\sum\limits_{j \in S}p_{ij}^{(n)}(t_m)=1$ ### 12.1.4 离散参数的齐次马尔可夫链 ##### 定义 设离散参数马尔可夫链 $\{X(t), t = t_0, t_1, t_2, ..., t_n, ...\}$ 如果一步转移概率 $p_{ij}(t_m)$ 不依赖于参数 $t_m$，即对任意两个不等的参数 $t_m$ 和 $t_k,m\ne k$，有

p{ij}(t_m)=p{ij}(tk)=p{ij}

则称此马尔可夫链具有**齐次性**或**时齐性**，称 $X(t)$ 为离散参数的齐次马尔可夫链。 ##### 例 Pasted image 20241218102752.png|575 Pasted image 20241218102804.png|575 ## 12.2 参数离散的齐次马尔可夫链 ### 12.2.1 转移概率矩阵 ##### 定义 设 $\{X(t), t = t_0, t_1, t_2, ..., t_n, ...\}$ 是齐次马尔可夫链，由于状态空间 $S$ 是离散的，不妨设 $S=\{0, 1, 2, ...,n, ...\}$ 则对 $S$ 内的任意两个状态 $i$ 和 $j$，由转移概率 $p_{ij}=P\{X(t_{m+1})=j|X(t_m)=i\}$ 排序一个矩阵：

P=
\left(
\begin{array}
&p{00}&p{01}&\cdots&p{0j}&\cdots\
p{10}&p{11}&\cdots&p{1j}&\cdots\
\vdots&\vdots&\ddots&\vdots&\cdots\
p{i0}&p{i1}&\cdots&p_{ij}&\cdots\
\vdots&\vdots&\vdots&\vdots&\ddots
\end{array}
\right)

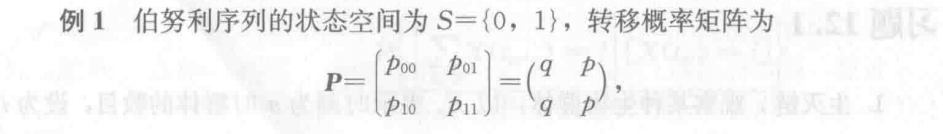
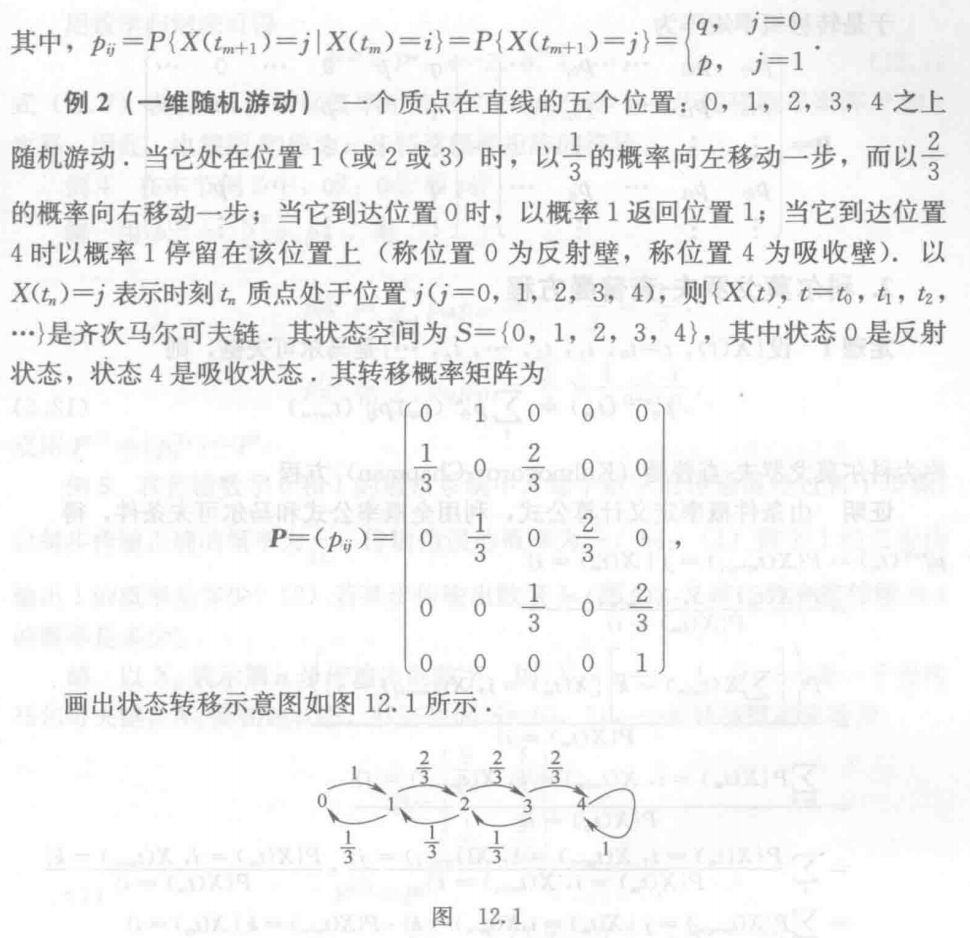
**称为（一步）转移概率矩阵**。 ##### （一步）转移概率矩阵的性质 1. $p_{ij}\geq 0$ 即元素均非负 2. $\sum\limits_{j\in S}p_{ij}=1$ 即每行和为 $1$ 具有以上两个性质的方阵称为**随机矩阵**，转移概率矩阵就是一个随机矩阵。 ##### 例 Pasted image 20241218111325.png|575 Pasted image 20241218111340.png|575 Pasted image 20241218111359.png|575 Pasted image 20241218111421.png|575 ### 12.2.2 科尔莫戈罗夫-查普曼方程 ##### 定理 设 $\{X(t), t=t_0, t_1, t_2, ..., t_n, ...\}$ 是参数离散的马尔可夫链，$S$ 为其状态空间，则有：

p{ij}^{(n+l)}(t_m)=
\sum\limits{k \in S} p{ik}^{(n)}(t_m) \cdot p^{(l)}{kj}(t_{m+n})

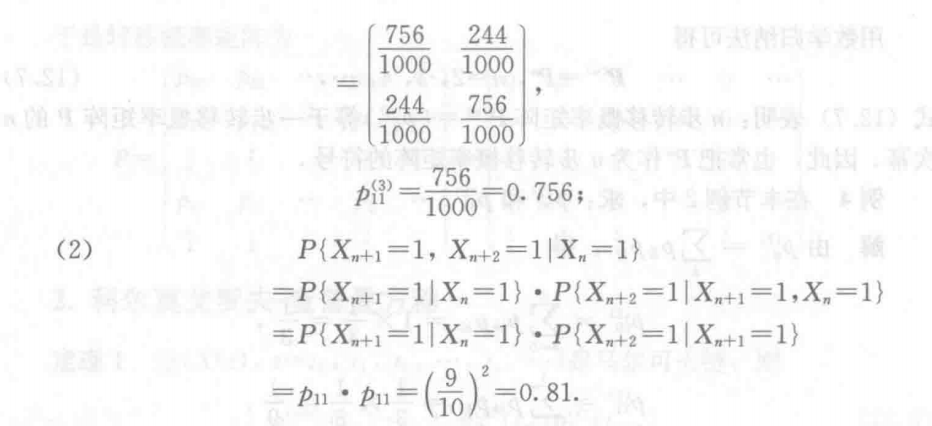称为**科尔莫戈罗夫-查普曼**方程。 ##### 注： 1. 如果马尔可夫链具有**齐次性**，那么 C-K 方程化为：$p_{ij}^{(n+l)}=\sum\limits_{k \in S} p_{ik}^{(n)} \cdot p^{(l)}_{kj}$ 2. 对于**齐次**马氏链，当 $n=l=1$ 时得到 $p_{ij}^{(2)}=\sum\limits_k p_{ik}p_{kj}$ 改写为矩阵形式得：$P^{(2)}=P^2$ 归纳得到 $P^{(n)}=P^n,\space n=2,3,...$ ##### 例 Pasted image 20241218111612.png|625 Pasted image 20241218111622.png|625 Pasted image 20241218111638.png|625 ### 12.2.3 有限维概率分布 #### 1. 初始分布（初始概率） 马氏链 $\{X(t), t = t_0, t_1, t_2, ...\}$ 在初始时刻 $t_0$ 的一维概率分布：

p_{j}(t_0)=P{X(t_0)=j}, \quad j=0, 1, 2, ...

#### 2. $n$ 维概率分布 设**齐次马尔可夫链**的参数集和状态空间都是非负整数集。 ##### 定理 设齐次马尔可夫链 $\{X(n), n=0,1,2,...\}$ 的状态空间 $S=\{0, 1, 2, ...,i, ...\}$，则对 $T$ 内任意 $n$ 个非负整数 $k_1<k_2<...<k_n$ 和 $S$ 内的任意 $n$ 个状态 $j_1, j_2, ...,j_n$，有：

\begin{aligned}
&P{X(k1) = j_1, X(k_2)=j_2, ..., X(k_n) = j_n}\
=& \sum\limits{i=0}^{+\infty}pi(0)\cdot p{ij1}^{(k_1)}\cdot p{j1j_2}^{(k_2 - k_1)}...p{j{n-1}j_n}^{(k_n-k{n-1})}
\end{aligned}

##### 例 Pasted image 20241218111822.png|600 #### 3. 绝对分布（绝对概率，瞬时概率） 马尔可夫链在任何时刻 $t_n$ 的一维概率分布：

p_j(t_n)=P{X(t_n)=j},\quad j = 0,1,2,...

齐次马尔可夫链在时刻的瞬时概率完全由初始分布和步转移概率所决定：

pj(t_n)=\sum\limits{i=0}^{+\infty} pi(t_0)\cdot p{ij}^{(n)},\quad j=0, 1, 2,...

向量形式：

\begin{aligned}
&\big(p_0(t_n), p_1(t_n), ..., p_j(t_n), ...\big)\
=&\big(p_0(t_0), p_1(t_0), ..., p_j(t_0), ...\big)\cdot P^n
\end{aligned}

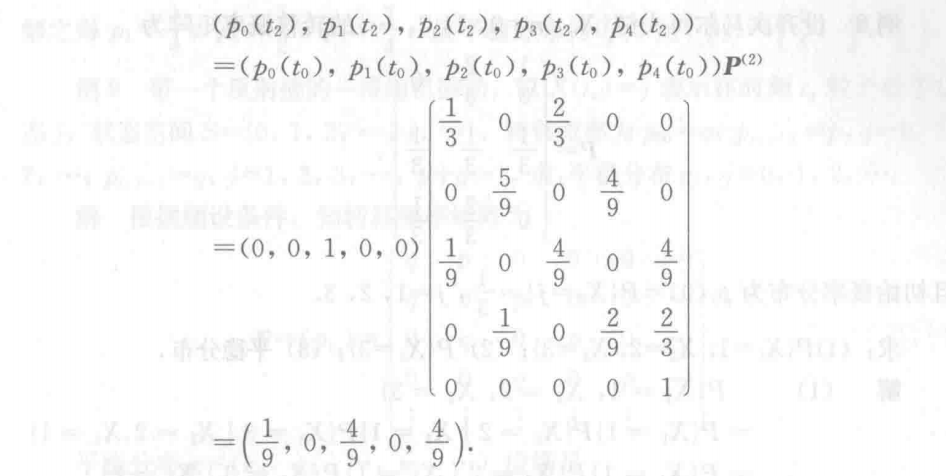其中n步转移概率矩阵 $P^{(n)} = (p_{ij}^{(n)}) = P^{n}$ 设 $\pi_{n} = (p_0(t_n),p_1(t_n),...,p_j(t_n),...)$，则有 $\pi_{n}=\pi_{n-1}P$，如果 $lim_{n\to+\infty}\pi_n=\pi$ 存在，则 $\pi$ 应满足 $\pi = \pi P$ ##### 例 Pasted image 20241218112109.png|625 Pasted image 20241218112119.png|625 Pasted image 20241218112131.png|625 ### 12.2.4 平稳分布 ##### 定义 对于齐次马尔可夫链 $\{X(t), t = t_0, t_1, t_2, ...\}$，如果存在一维概率分布 $p_j\space j=1,2,...$，满足：

pj=\sum\limits{i=0}^{+\infty}pip{ij}

或

(p_0, p_1, p_2, ..., p_j, ...)=(p_0, p_1, p_2, ..., p_j, ...)\cdot P

则称 $p_j,\space j=0,1,2,...$ 为**平稳分布**，称 $X(t)$ 具有**平稳性**，是**平稳齐次马尔可夫链**。 显然有 $\pi = \pi P = \pi P^{(n)}$ ##### 定理 如果齐次马尔可夫链 $\{X(t), t=t_0, t_1, t_2,...\}$ 的初始分布 $p_j(t_0)=P\{X(t_0)=j\},\space j=0,1,2,...$ 是一个平稳分布，则对 $\forall n$

p_j(t_n) = P{X(t_n)=j}=p_j(t_0),\space j=0,1,2,...

\big(p_0(t_n), p_1(t_n), ..., p_j(t_n), ...\big)
=\big(p_0(t_0), p_1(t_0), ..., p_j(t_0), ...\big)

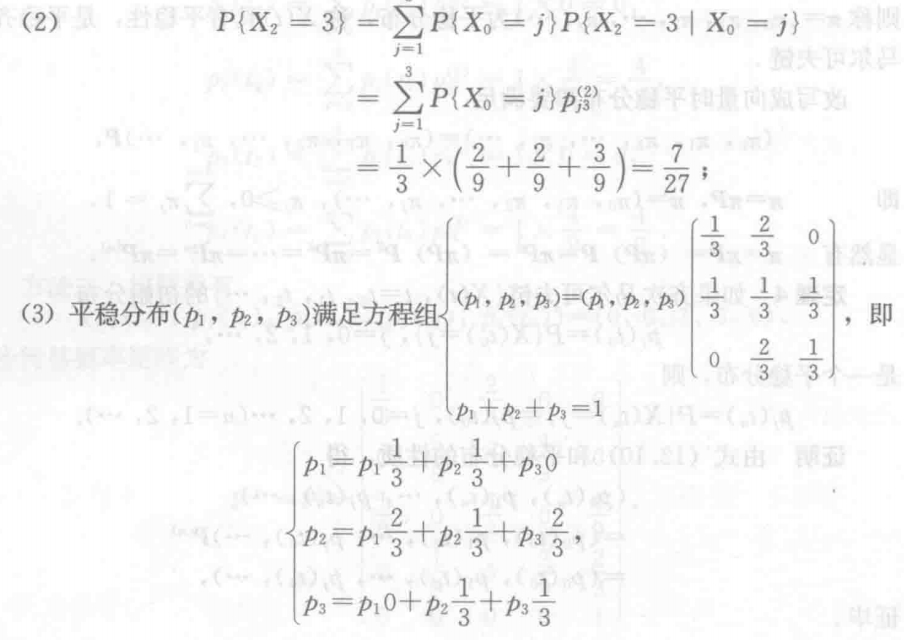
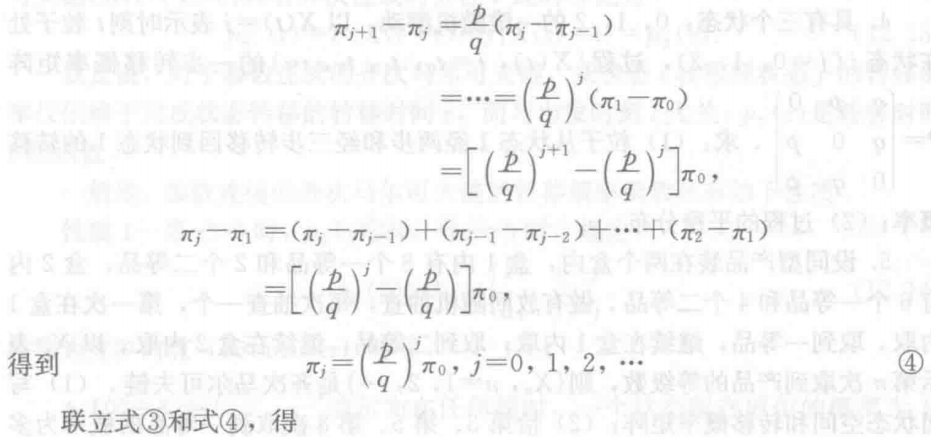
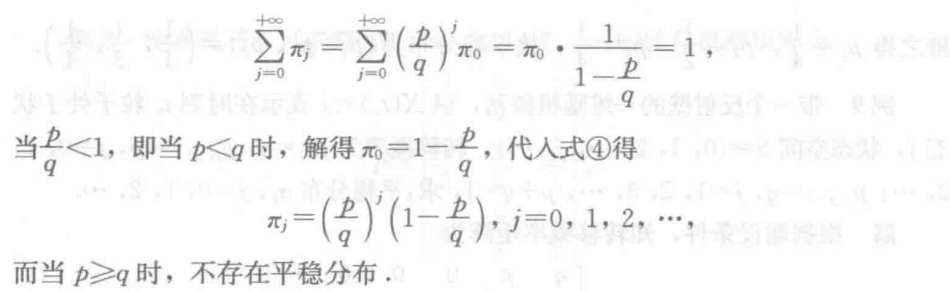是一个严平稳时间序列。 ##### 例 Pasted image 20241218112403.png|550 Pasted image 20241218112413.png|550 Pasted image 20241218112424.png|550 Pasted image 20241218112432.png|550 Pasted image 20241218112439.png|550 ## 12.3 参数连续的齐次马尔科夫链 ### 12.3.1 转移概率函数 ##### 定义：转移概率和转移时间 设 $\{X(t),t\ge 0\}$ 是参数连续的马尔科夫链，对于任意非负实数 $t$ 和任意正实数 $\tau$ ，以及链的任意两个状态 $i,j$，条件概率 $$P\{X(t+\tau) = j|X(t) = i\} = p_{ij}^{(r)}(t)$$ 称为马尔科夫链在时刻 $t$ 由状态 $i$ 出发，经过时间间隔 $\tau$ ，在时刻 $t+\tau$ 到达状态 $j$ 的**转移概率**，$\tau$ 称为**转移时间**。 ##### 定义：齐次性或时齐性 如果 $p_{ij}^{(r)}(t)$ 不依赖于出发时刻 $t$，仅依赖于转移时间 $\tau$，则称马尔科夫链 $\{X(t),t\ge 0\}$ 具有**齐次性**或**时齐性**，此时可记为 $$p_{ij}^{(r)}(t) = P\{X(t+\tau) = j|X(t) = i\} = p_{ij}(\tau)$$ ##### 齐次马尔可夫链的性质 1. 当 $\tau >0$ 时，$p_{ij}(\tau)\ge 0$。当 $\tau = 0$ 时，规定

p{ij}(0) = \delta{ij} =
\begin{cases}
1, &{i = j} \
0, &{i\neq j}
\end{cases}

称为克罗内克符号。此性质表示在任何瞬间，一个状态留在原位的概率为，而跳离原位的概率为，是状态空间满足科尔莫戈罗夫查普曼方程，即

p{ij}(\tau_1+\tau_2) =\sum\limits{k\in S}p{ik}(\tau_1)\cdot p{kj}(\tau_2),\ \tau_1>0,\ \tau_2>0

（实际上是规定）转移概率函数在处右连续。当充分小时，齐次马尔可夫链的状态几乎滞留原位，不发生转移

lim{r\to 0^+}p{ij}(\tau) = p_{ij} (0) =
\begin{cases}
1, &{i=j} \
0, &{i\neq j}
\end{cases}

### 12.3.2 转移速率矩阵 ##### 定义：转移速率/转移密度 如果齐次马尔可夫链的转移概率函数 $p_{ij}(\tau)$ 在 $\tau= 0$ 的右导数存在，即存在

p{ij}'(0) = lim{r\to 0^+} \frac{p{ij}(\tau)-p{ij}(0)}{\tau} = q_{ij}

则称导数值 $q_{ij}$ 为由状态 $i$ 转移到状态 $j$ 的**转移速率**，或称**转移密度**。 ##### 定义：转移速率矩阵/转移密度矩阵/Q阵 不妨设状态空间 $S$ 为非负整数集，以 $q_{ij}$ 为元素的矩阵

Q=
\left(
\begin{array}
&q{00}&q{01}&\cdots&q{0j}&\cdots\
q{10}&q{11}&\cdots&q{1j}&\cdots\
\vdots&\vdots&\ddots&\vdots&\cdots\
q{i0}&q{i1}&\cdots&q_{ij}&\cdots\
\vdots&\vdots&\vdots&\vdots&\ddots
\end{array}
\right)

称为**转移速率矩阵**，或称**转移密度矩阵**，简称**Q阵** ##### 转移速率的性质 1. $q_{ij}\ge 0, i\neq j, q_{ii}\le 0$ 2. 当状态空间为有限集时， $q_{ij}$ 满足 $\sum\limits_{j\in S}q_{ij} = 0$ 当状态空间 $S$ 为无限集时，不一定成立，一般有 $\sum\limits_{j\in S}q_{ij} \le 0$ ##### 例 Pasted image 20241218150703.png|575 Pasted image 20241218150717.png|575 ### 12.3.3 科尔莫戈罗夫方程 设 $\{X(t),t\ge 0\}$ 是参数连续的齐次马尔科夫链，转移概率函数 $p_{ij}(\tau)$，转移速率矩阵 $Q = (q_{ij})$ 。分别以 $p_{ij}(\tau)$ 为元素和以 $p_{ij}/(\tau)$ 为元素构造矩阵 $P(\tau) = [p_{ij}(\tau)],\ P'(\tau) = [p'_{ij}(\tau)]$ 。则有 ##### 科尔莫戈罗夫前进方程 若对状态 $j$，$\sum\limits_{i\neq j}q_{ij}<+\infty$ ，则转移概率函数 $p_{ij}(\tau)$ 满足微分方程

p{ij}'(\tau) = \sum\limits{k\in S}p{ik}(\tau)q{kj}

该方程称为**科尔莫戈罗夫前进方程**，$S$ 为状态空间 科尔莫戈罗夫前进方程写成矩阵微分方程形式分别为 $P'(\tau) = P(\tau)Q$ ##### 科尔莫戈罗夫后退方程 若对状态 $i$，$\sum\limits_{j\neq i}q_{ij}<+\infty$ ，则转移概率函数 $p_{ij}(\tau)$ 满足微分方程

p{ij}'(\tau) = \sum\limits{k\in S}q{ik}p{kj}(\tau)

该方程称为**科尔莫戈罗夫后退方程**，$S$ 为状态空间 科尔莫戈罗夫后退方程写成矩阵微分方程形式分别为 $P'(\tau) = QP(\tau)$ ##### 例 Pasted image 20241218151719.png|575 ### 12.3.4 瞬时概率
Built with MDFriday ❤️