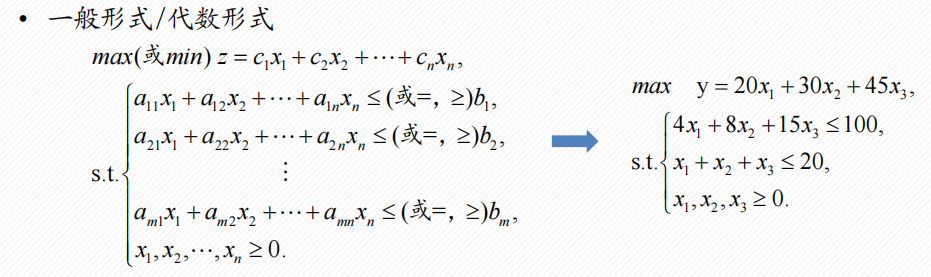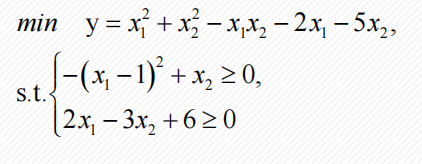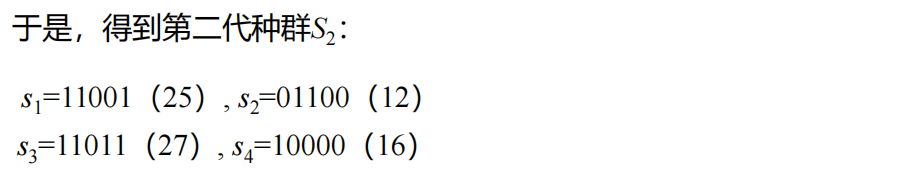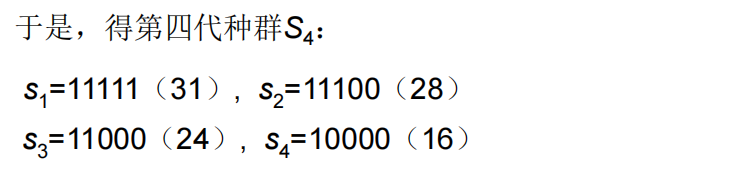B
- 动态优化 > 模糊综合评价。博弈论。多目标优化
- 优化和评价( TOPSIS/熵权 )综合在一起(?)
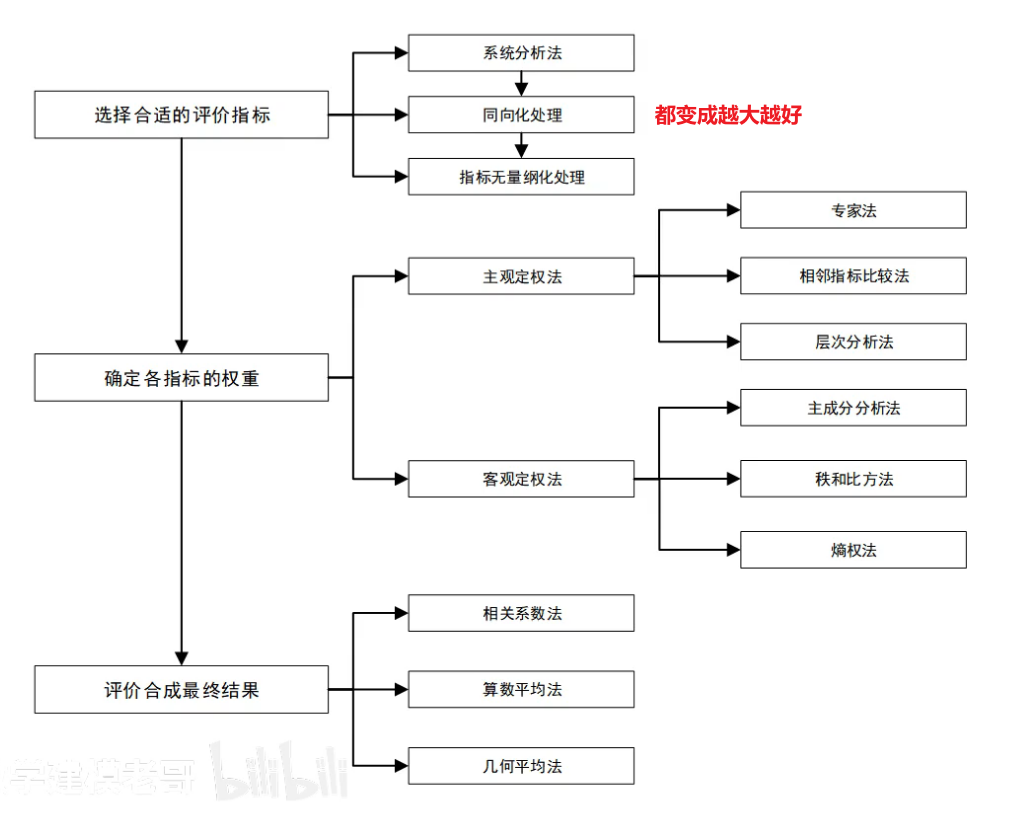
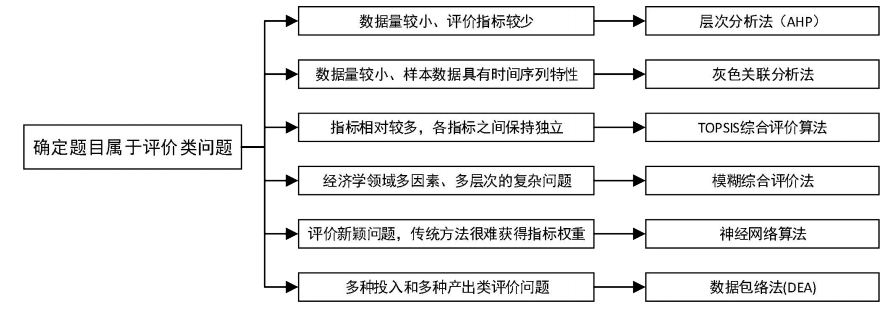
1 评价类
评价或选择一个可能更好或更优的政策或方案,要先找到指标,再量化指标,再综合考虑所有指标
层次分析法
- 一致性检验 (
- 求权重
- 算术平均法
- 几何平均法
- 特征值法
熵权法
- 正向矩阵标准化
- 计算概率矩阵P
- 计算熵权
主成分分析
目的:减少特征(降维)
8) 解释主成分
TOPSIS法
- 原始矩阵正向化(所有指标转化为极大型指标)
- 正向矩阵标准化(消除不同指标量纲的影响)
- 用层次分析法(较主观)/熵权法(较客观)给指标加上权重
- 计算得分并归一化
模糊综合评价
把数据(如成本、可采矿量等)通过隶属函数转化成评分
- 单层次
- 求隶属函数
- 求隶属度,获得单因素评判矩阵
- 求权重
- 综合评价
- 多层次
- 把前一级的
- 把前一级的
灰色关联分析
- 数据正向化
- 正向化后预处理(除以均值)
- 构造母序列(没有母序列时可以
- 计算关联系数
- 计算关联度
- 计算指标权重
- 计算得分并归一化
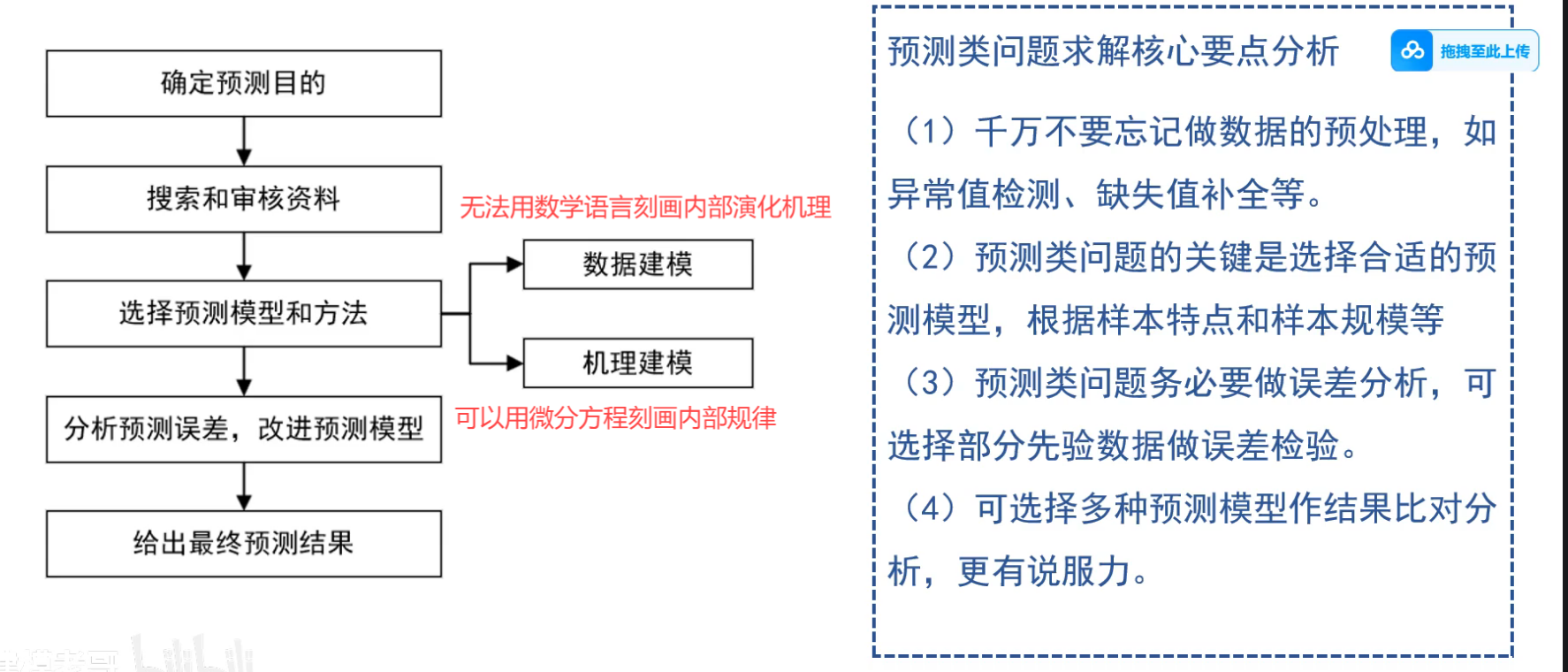
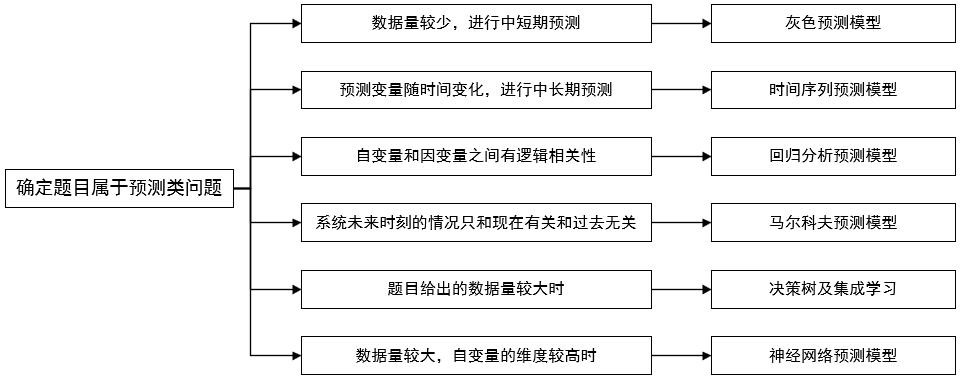
2 预测类
- 根据已知预测未知
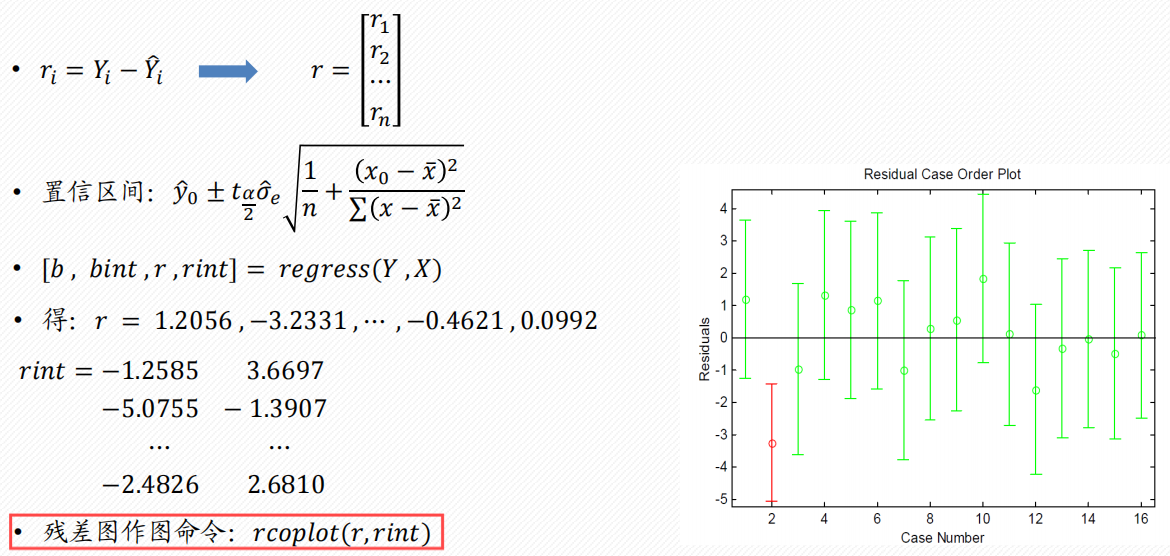
回归分析预测模型
一元线性回归分析
-
使用
regress函数
-
b
-
bint
-
r & rint
-
stats
多元线性回归分析
- 多元线性回归模型的参数估计
- 多元线性回归模型和回归系数的检验
- 多元线性回归模型的预测
普通方法 matlab
调用 regress 函数
逐步回归 matlab
- 先逐步回归判断哪个变量影响更大,删掉影响小的变量
- 对影响大的变量进行线性回归
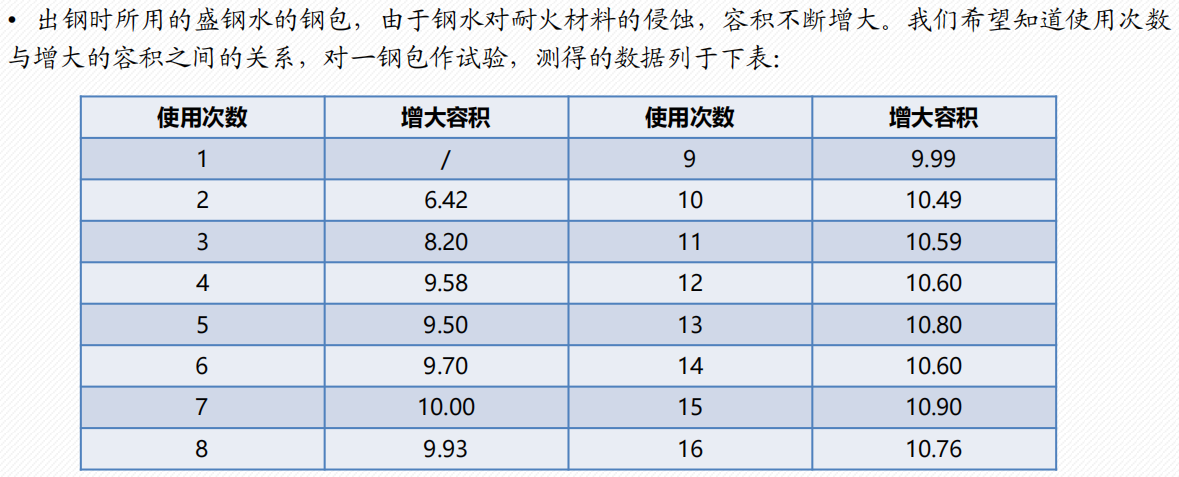
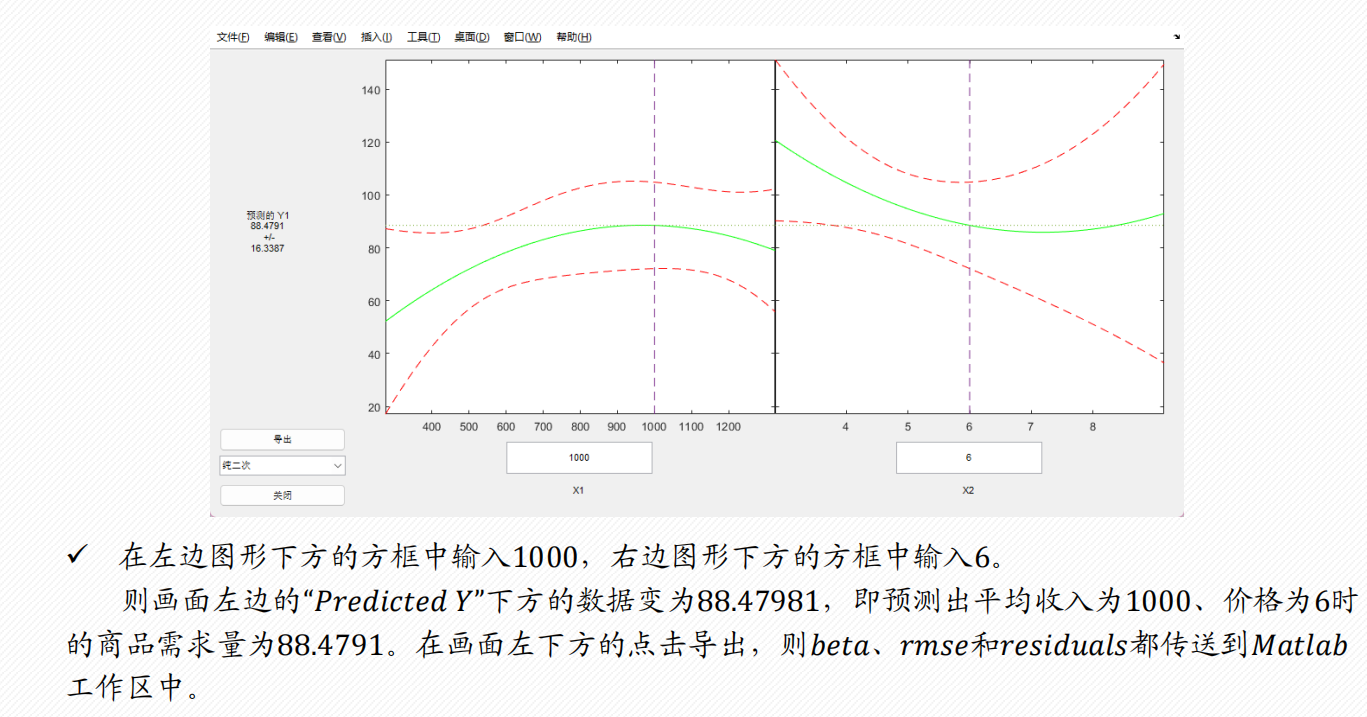
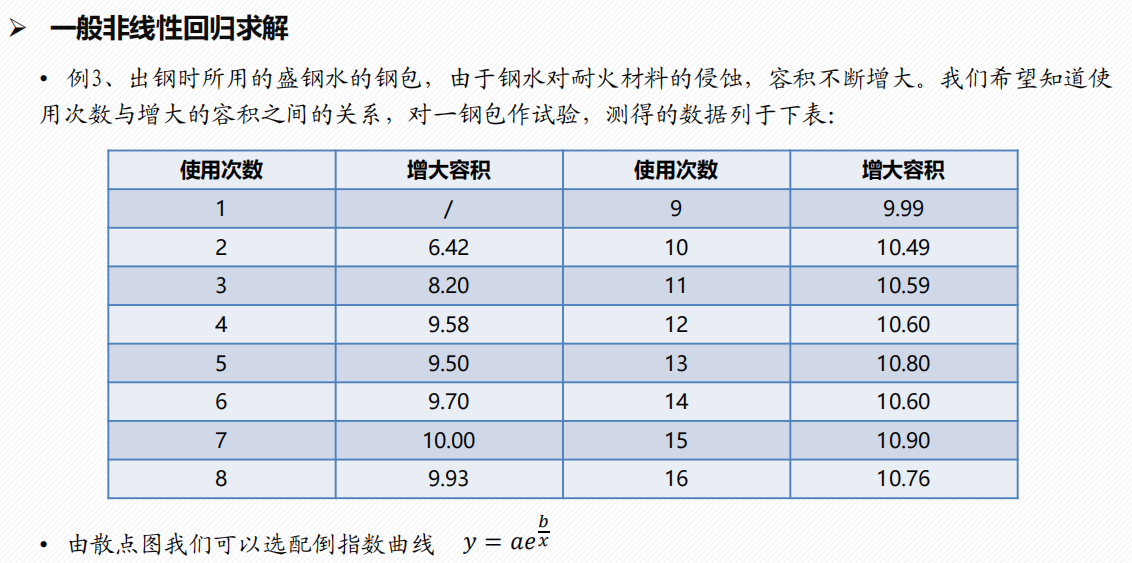
非线性回归分析
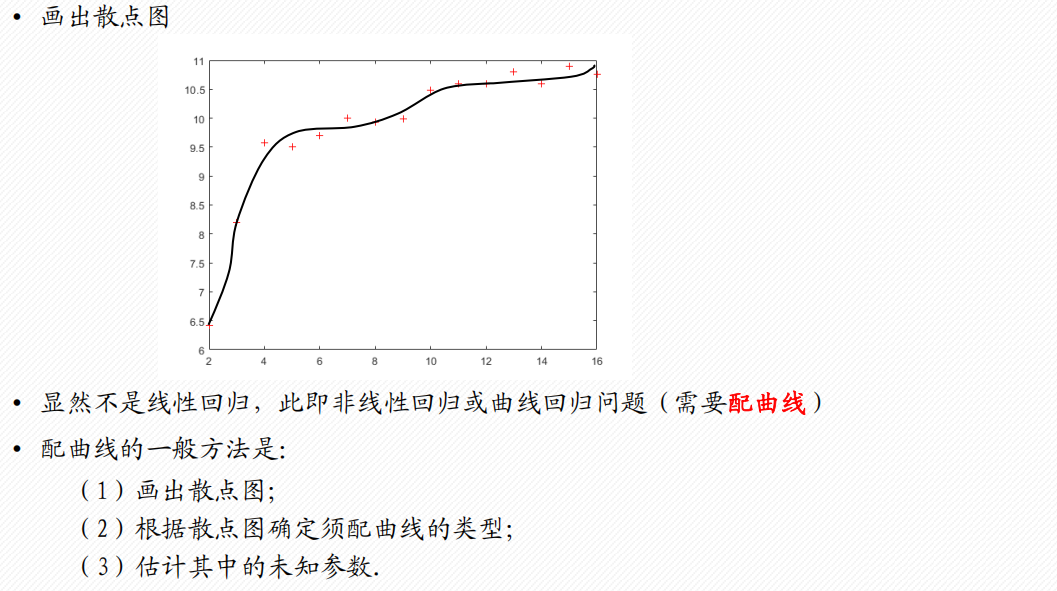
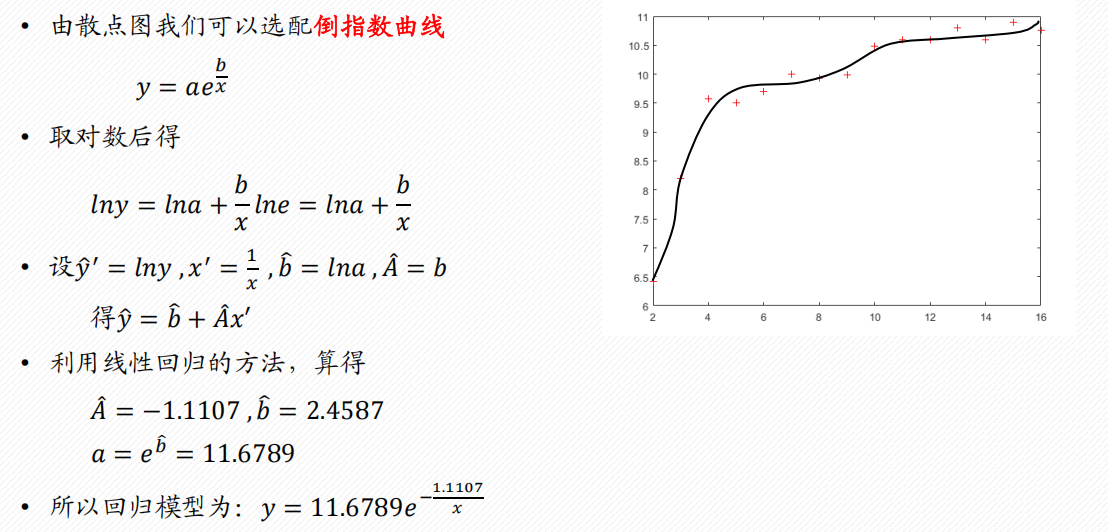
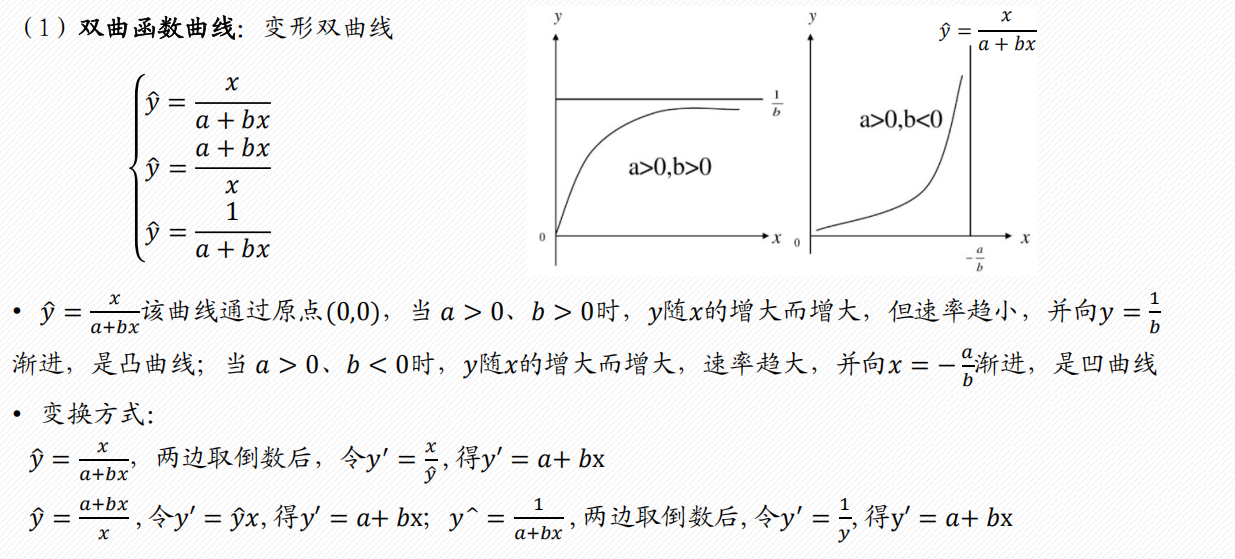
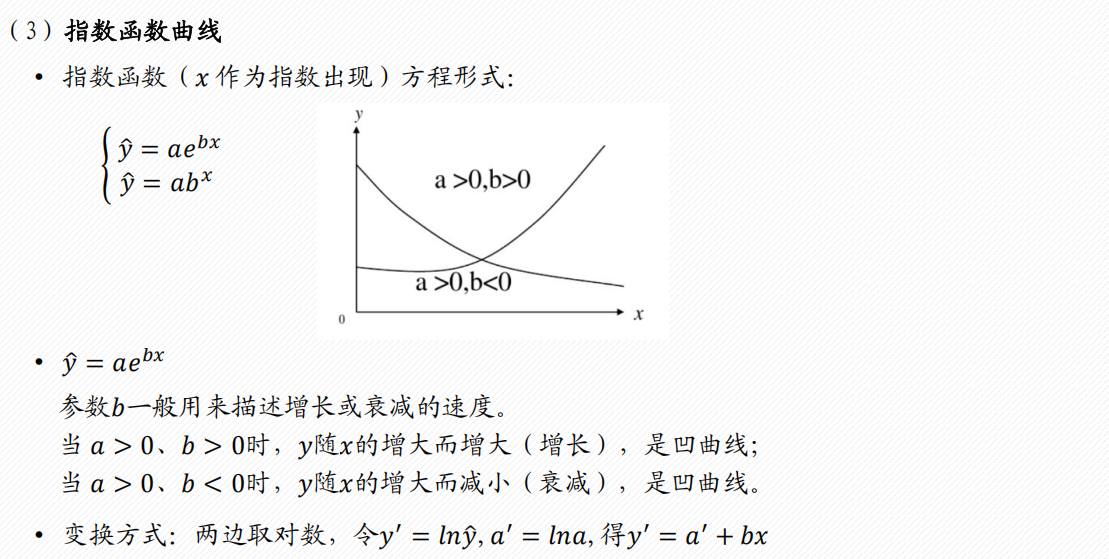
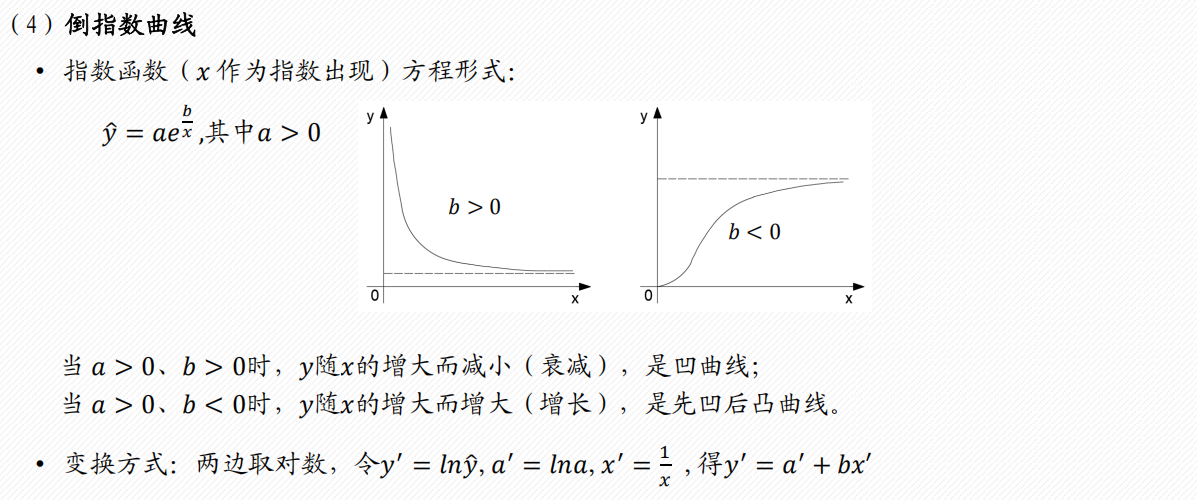
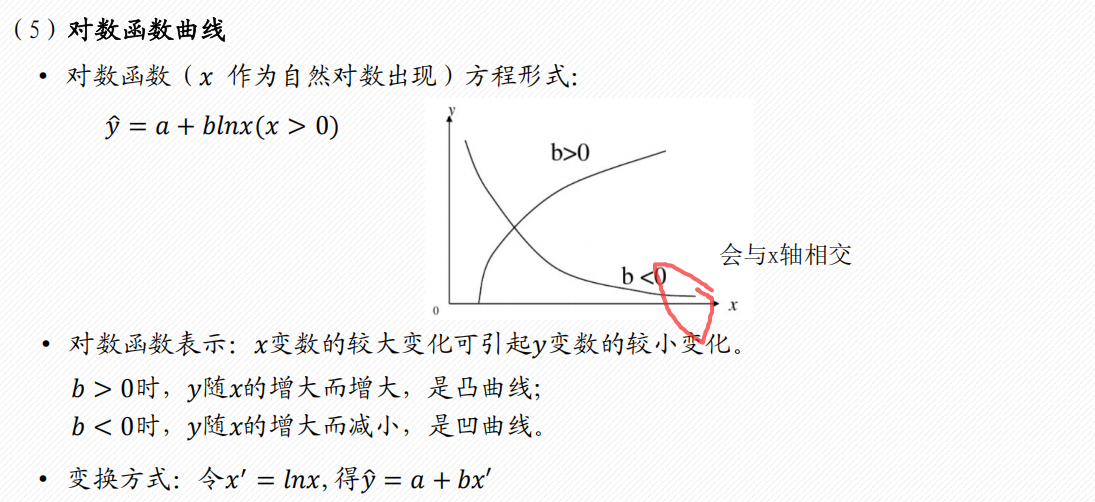
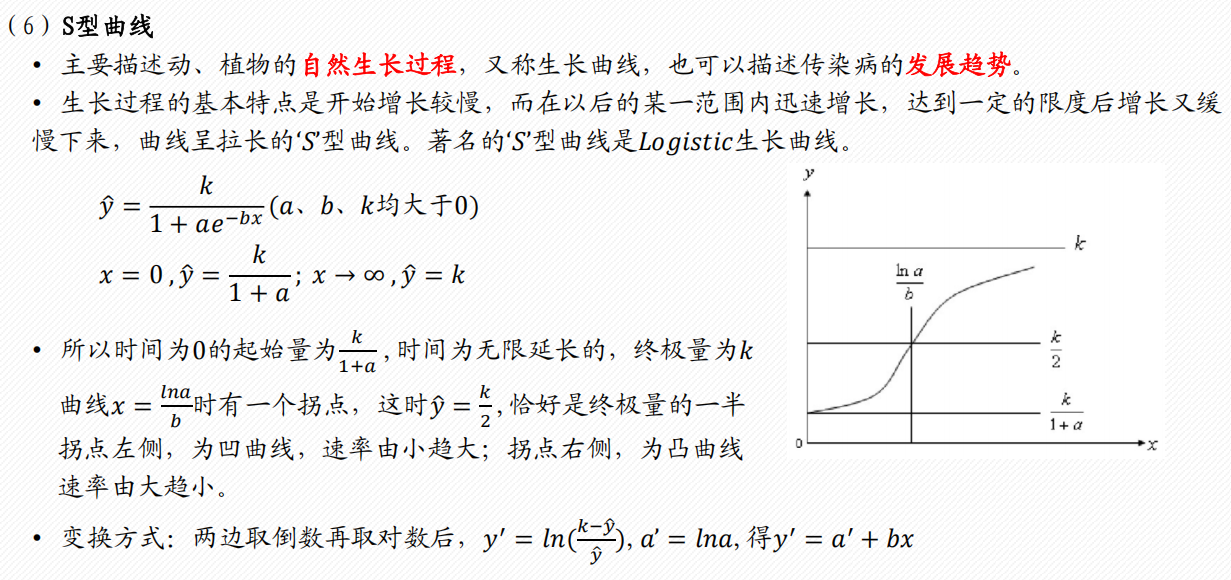
1 配曲线求解
常见的6类曲线
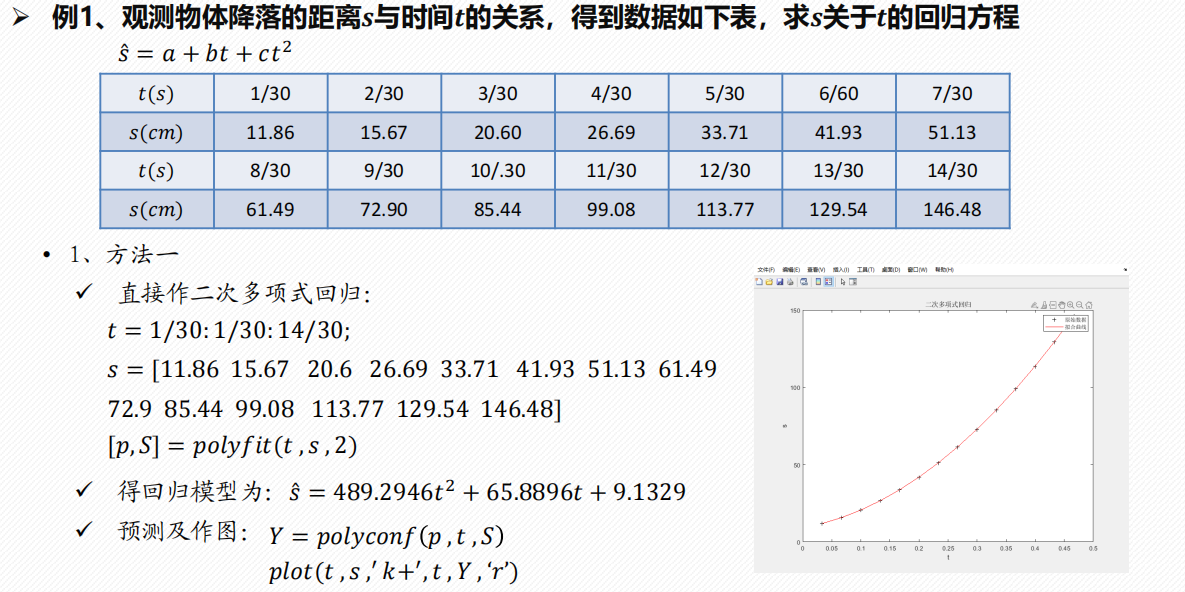
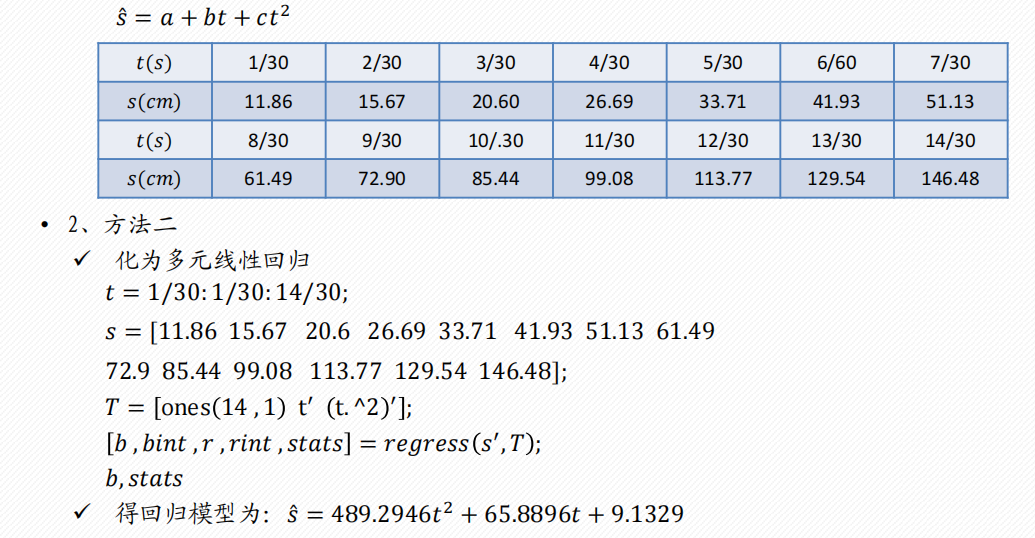
2 多项式回归
一元多项式回归
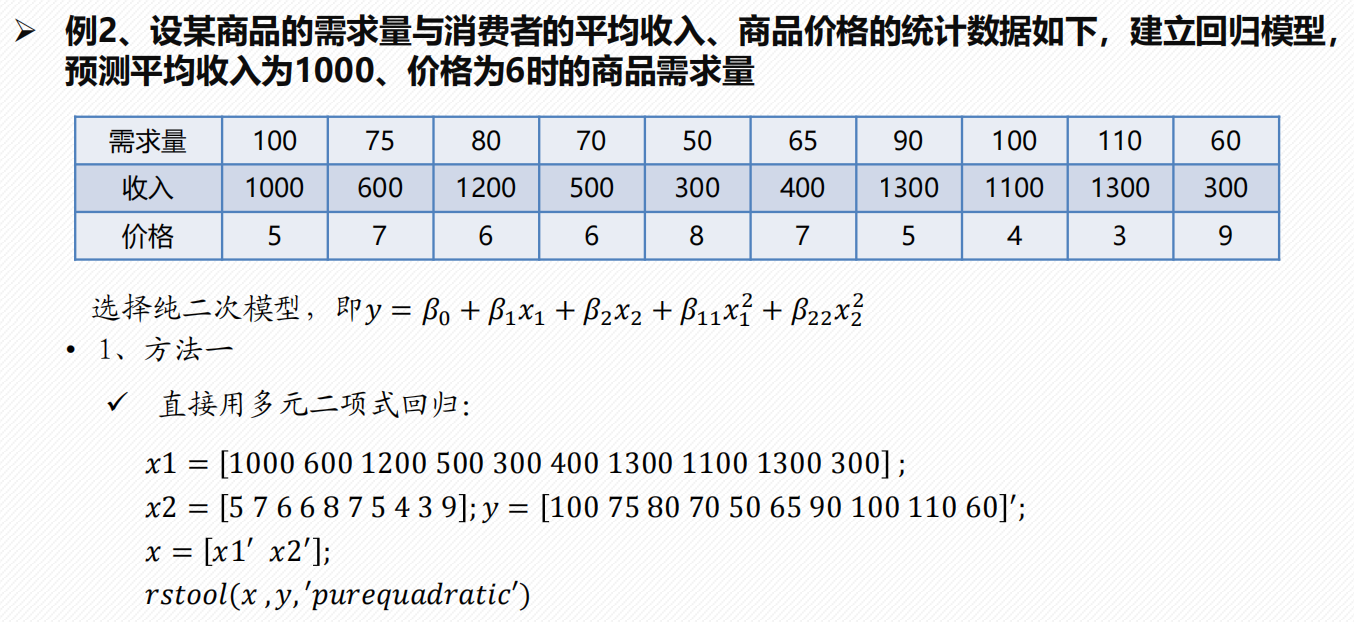
多元二项式回归
3 一般求解
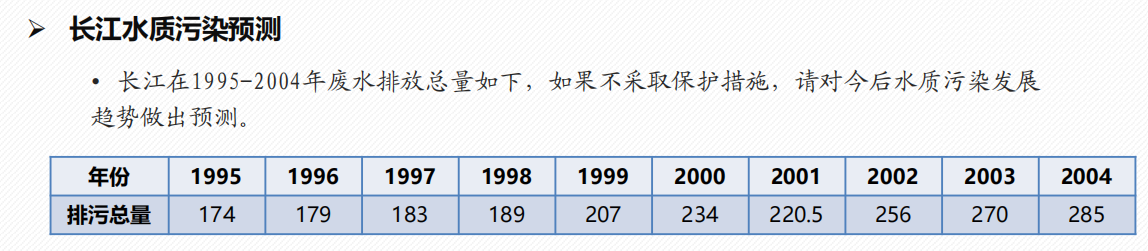
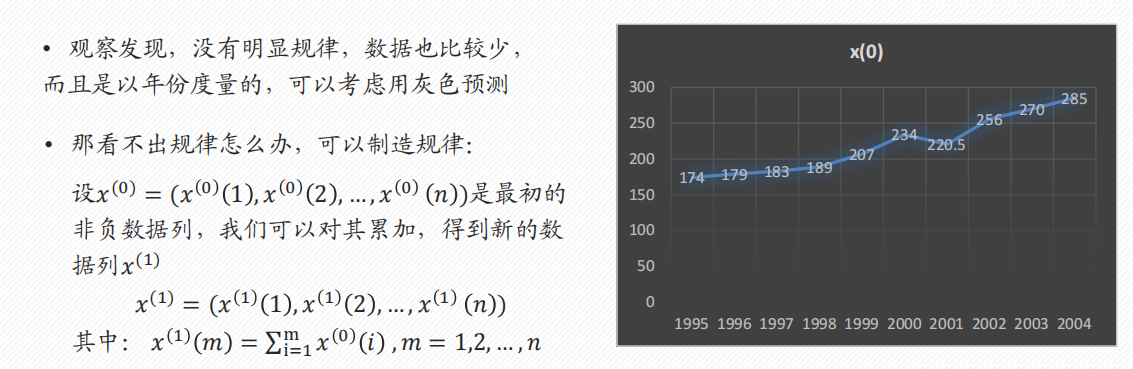
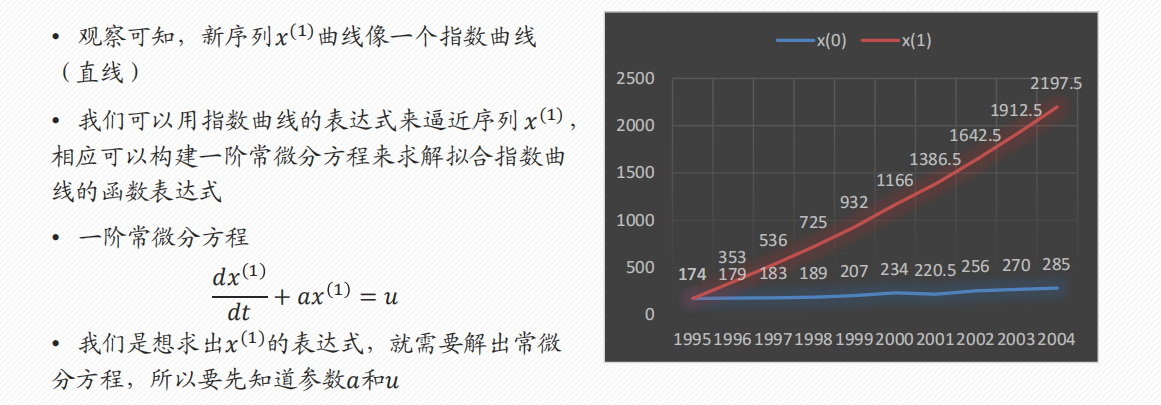
灰色预测 GM(1, 1)
- 灰色预测适用于什么情况?
- 数据是以年份度量的非负数据(如果是月份或者季度数据一般要用时间序列模型),比如定时求量的题目,即已知一些年份数据,预测下一年的数据,常见有GDP、人口数量、耕地面积、粮食产量等;或者定量求时,已知一些年份数据和某灾变的阈值,预测下次灾变时间。
- 数据能经过准指数规律的检验(除了前两期外,后面至少90%的期数的光滑比要低于0.5)。
- 数据的期数较短且和其他数据之间的关联性不强(小于等于10,也不能太短了,比如只有3期数据),要是数据期数较长,一般用传统的时间序列模型比较合适。
- 应该是时期时间序列而不是时点时间序列
模型求解前,判断能否使用灰色预测模型
模型求解
模型评价
时间序列模型 ( ARIMA )
时间序列根据时间和数值性质的不同,可以分为时期时间序列和时点时间序列
- 时期序列中,数值要素反映现象在一定时期内发展的结果
- 时点序列中,数值要素反映现象在一定时点上的瞬间水平
- 时期序列可加,时点序列不可加
模型介绍
自回归模型 ( AR(p) )
移动平均模型 ( MA(q) )
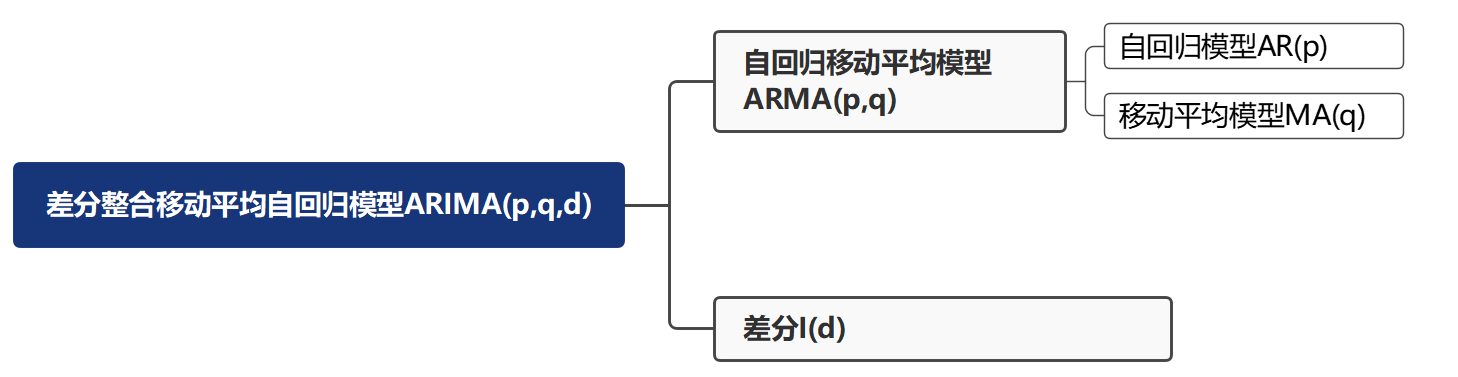
自回归移动平均模型 ( ARMA(p, q) )
差分自回归移动平均模型 ( ARIMA(p, d, q) )
建模步骤
1 实现/检验 平稳性
检验平稳性:
- 图检验法
- 时间序列趋势图
- 自相关函数图
- ADF 检验
不平稳怎么变平稳:
- 差分法(一般 1-2 次就够)
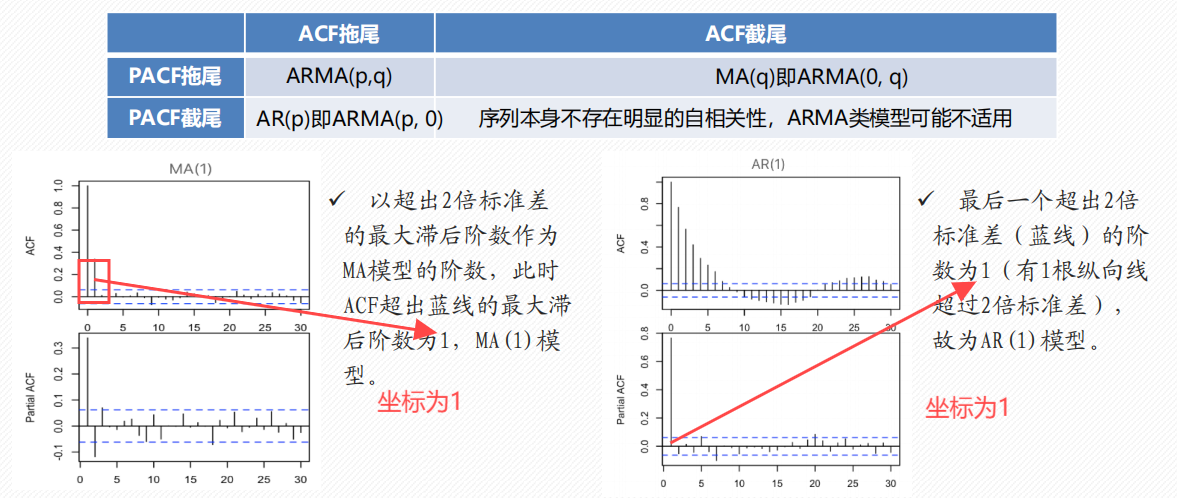
自相关系数 (ACF) 和偏自相关系数 (PACF)
- 自相关系数
- 偏自相关系数:剔除中间 k-1 个随机变量的干扰,只考虑
ADF检验
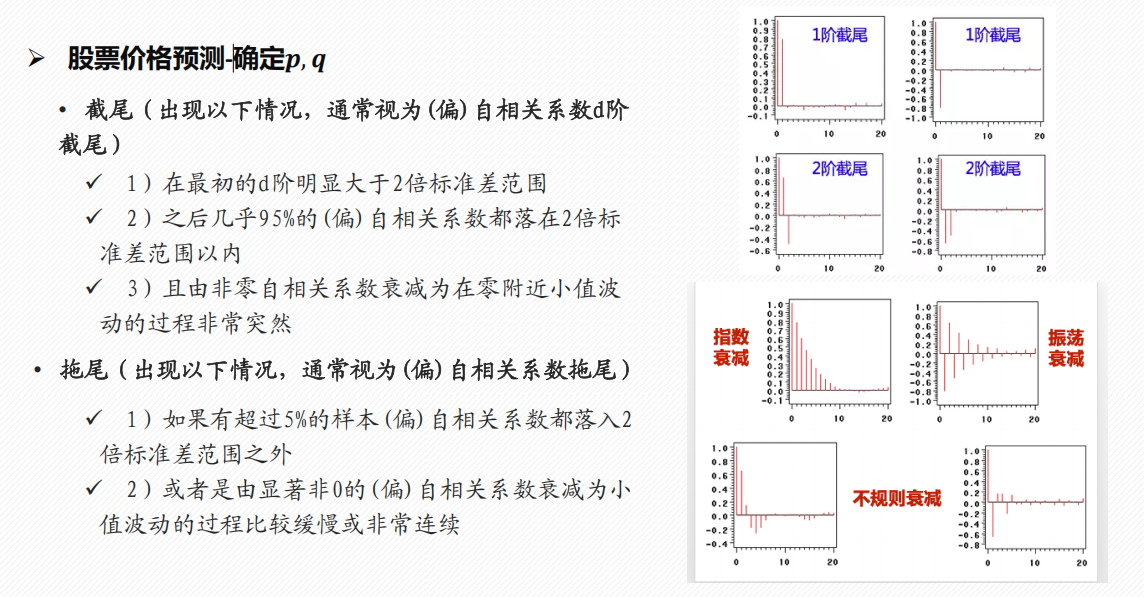
2 确定 p, q, d
- d:差分次数(一般为0, 1, 2)
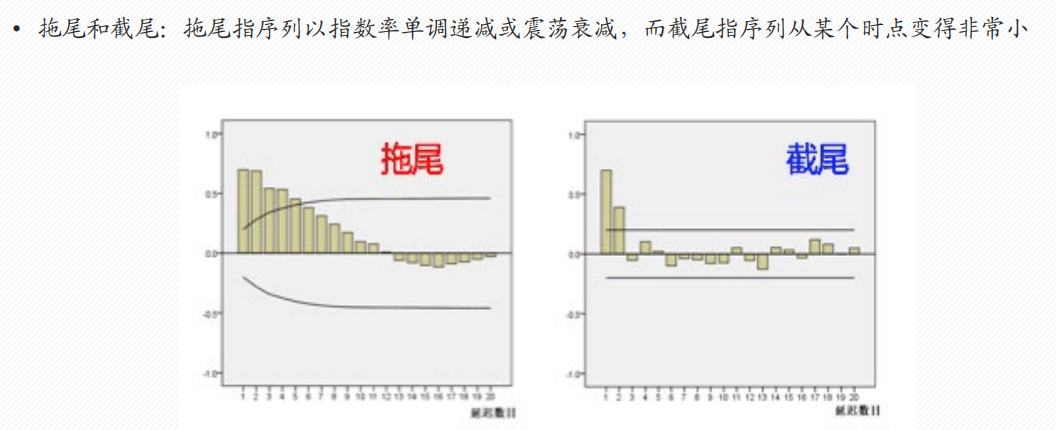
法1:ACF/PACF 截尾/拖尾判断
法2:AIC BIC准则(更客观)
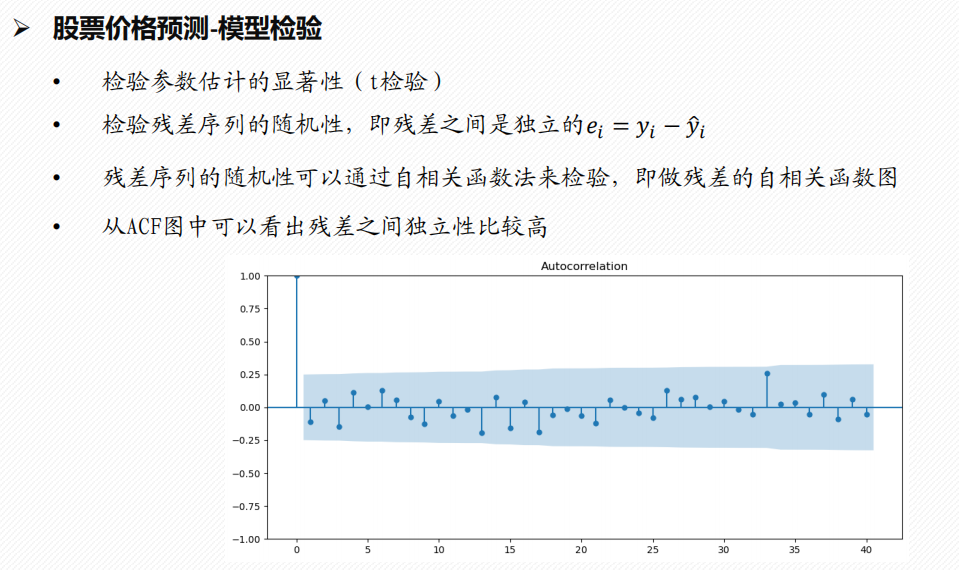
3 模型检验
4 模型预测
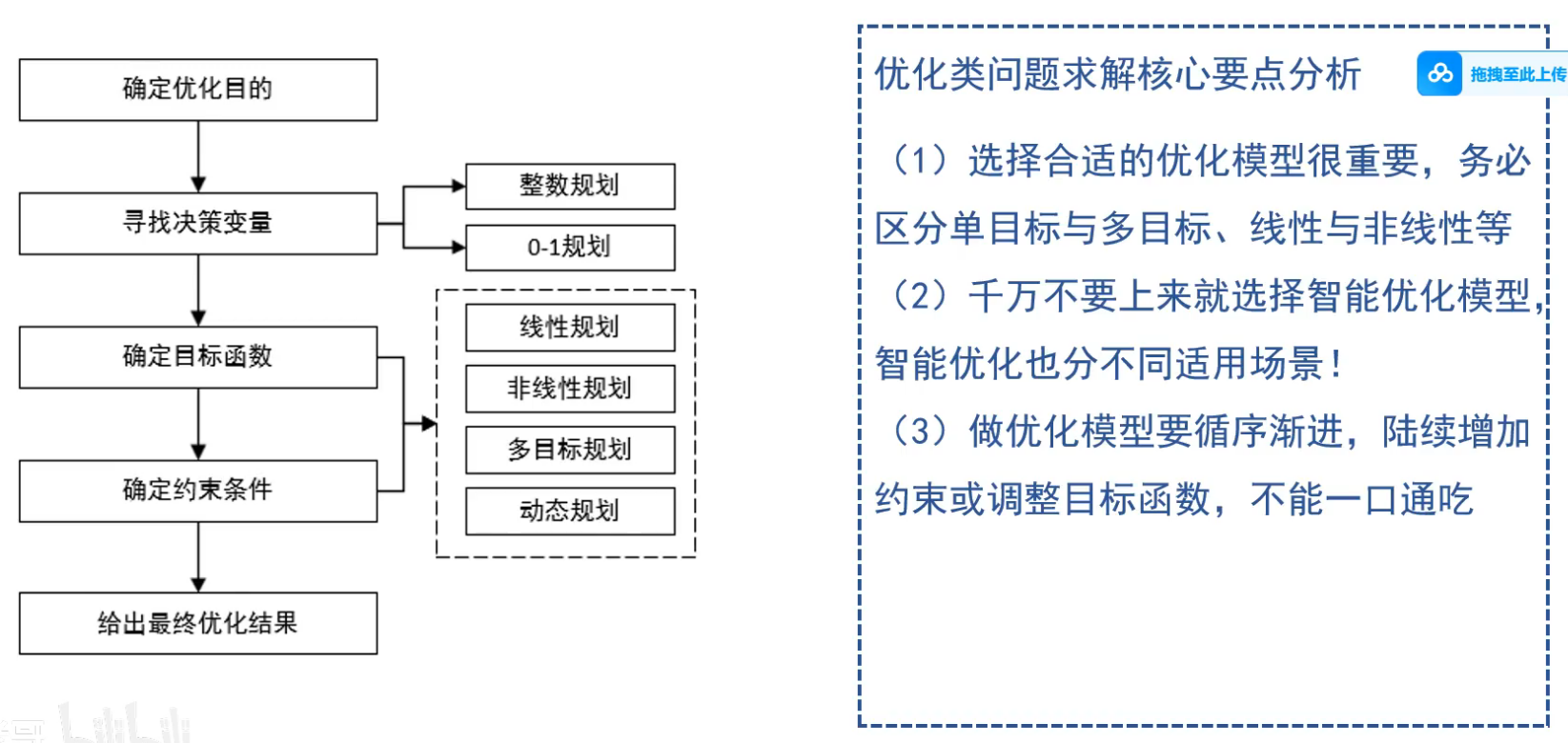
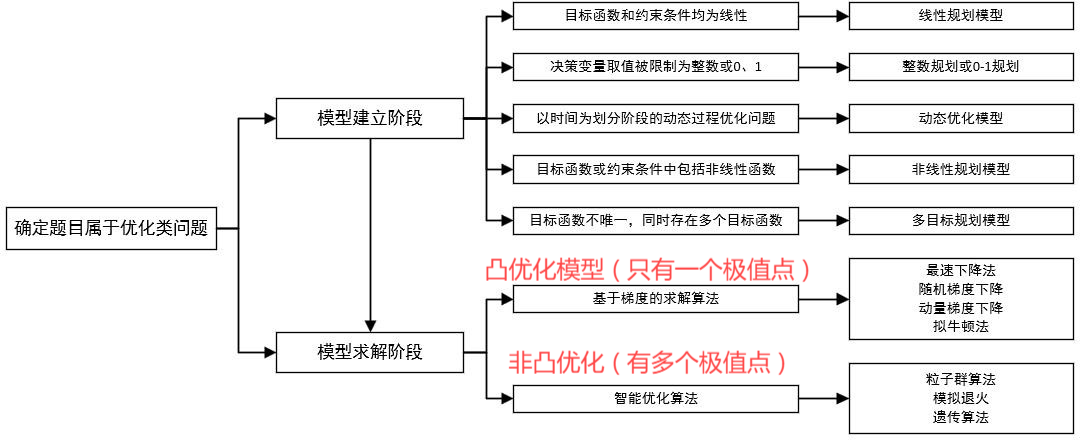
3 优化类
找最大/最小/极值
1 线性规划法
-
目标函数和约束条件都是决策变量的线性函数,即不存在
-
线性规划模型:在一组线性约束条件下,求线性目标函数的最大值或最小值
-
多目标规划:把其中一个目标转化为约束条件进行求解
建模步骤
线性规划的表现形式
关于python代码
2 蒙特卡罗法
- 定义:蒙特卡罗法又称统计模拟法,是一种随机模拟方法,以概率和统计理论方法为基础的一种计算方法,是使用随机数(或更常见伪随机数)来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解。
- 是一种思想而不是算法,没有固定的代码
- 非线性规划用蒙特卡罗法求初始值是最精确的
3 非线性规划法
1 matlab
例1
%% code1.m
%% 非线性规划的函数
% [x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlfun,option)
% x0表示给定的初始值(用行向量或者列向量表示),必须得写
% A b表示线性不等式约束
% Aeq beq 表示线性等式约束
% lb ub 表示上下界约束
% fun表示目标函数
% nonlfun表示非线性约束的函数
% option 表示求解非线性规划使用的方法
clear;clc
format long g %可以将Matlab的计算结果显示为一般的长数字格式(默认会保留四位小数,或使用科学计数法)
%% 例题1的求解
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
% s.t. -(x1-1)^2 +x2 >= 0 ; 2x1-3x2+6 >= 0
x0 = [0 0]; %任意给定一个初始值
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1) % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下
fval = -fval
%% 使用其他算法对例题1求解
% Matlab默认使用的算法是'interior-point' 内点法
% 使用interior point算法 (内点法)
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% 使用SQP算法 (序列二次规划法)
option = optimoptions('fmincon','Algorithm','sqp')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval %得到-4.358,远远大于内点法得到的-1,猜想是初始值的影响
% 改变初始值试试
x0 = [1 1]; %任意给定一个初始值
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option) % 最小值为-1,和内点法相同(这说明内点法的适应性要好)
fval = -fval
%% 使用蒙特卡罗的方法来找初始值(推荐)
clc,clear;
n=10000000; %生成的随机数组数
x1=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin=+inf; % 初始化函数f的最小值为正无穷(后续只要找到一个比它小的我们就对其更新)
for i=1:n
x = [x1(i), x2(i)]; %构造x向量, 这里千万别写成了:x =[x1, x2]
if ((x(1)-1)^2-x(2)<=0) & (-2*x1(i)+3*x2(i)-6 <= 0) % 判断是否满足条件
result = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ; % 如果满足条件就计算函数值
if result < fmin % 如果这个函数值小于我们之前计算出来的最小值
fmin = result; % 那么就更新这个函数值为新的最小值
x0 = x; % 并且将此时的x1 x2更新为初始值
end
end
end
disp('蒙特卡罗选取的初始值为:'); disp(x0)
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)
fval = -fval
%% fun1.m
function f = fun1(x)
% 注意:这里的f实际上就是目标函数,函数的返回值也是f
% 输入值x实际上就是决策变量,由x1和x2组成的向量
% fun1是函数名称,到时候会被fmincon函数调用, 可以任意取名
% 保存的m文件和函数名称得一致,也要为fun1.m
% min f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
f = x(1)^2+x(2)^2 -x(1)*x(2)-2*x(1)-5*x(2) ;
end
%% nonlfun1.m
function [c,ceq] = nonlfun1(x)
% 注意:这里的c实际上就是非线性不等式约束,ceq实际上就是非线性等式约束
% 输入值x实际上就是决策变量,由x1和x2组成的一个向量
% 返回值有两个,一个是非线性不等式约束c,一个是非线性等式约束ceq
% nonlfun1是函数名称,到时候会被fmincon函数调用, 可以任意取名,但不能和目标函数fun1重名
% 保存的m文件和函数名称得一致,也要为nonlfun1.m
% -(x1-1)^2 +x2 >= 0
c = [(x(1)-1)^2-x(2)]; % 千万別写成了: (x1-1)^2 -x2
ceq = []; % 不存在非线性等式约束,所以用[]表示
end
例2
%% xuanzhiwenti.m
%%%第一问:线性规划
clear;clc;
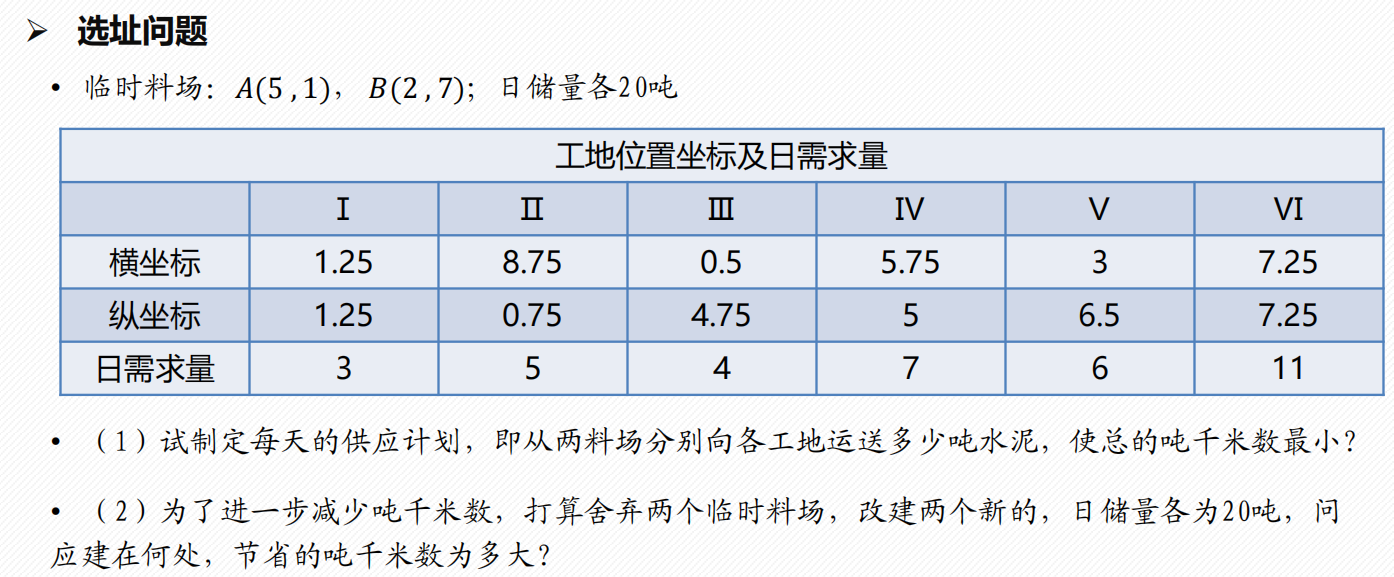
% 6个工地坐标
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
% 临时料场位置
x=[5 2];
y=[1 7];
% 6个工地水泥日用量
d=[3 5 4 7 6 11];
% 计算目标函数系数,即6工地与两个料场的距离,总共12个值
for i=1:6 % 对于6个工地
for j=1:2 % 接收两个料场的供用
l(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2); % 距离
end
end
f = [l(:,1);l(:,2)]; % 目标函数系数向量,总共12个值
% 不等式约束条件的变量系数和常数项
% 双下标转换成单下标:x11=x1,x21=x2,x31=x3,x41=x4,…,x62=x12
A = [1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1];
% 两个临时料场日储量
b = [20;20];
% 矩阵的行数是约束条件个数,列数是变量个数
% 等式约束的变量系数和常数项
Aeq = [eye(6),eye(6)]; % 两个单位矩阵横向拼成
beq=[d(1);d(2);d(3);d(4);d(5);d(6)];
% 所有变量下限全是0
Vlb=[0 0 0 0 0 0 0 0 0 0 0 0];
[x,fval]=linprog(f,A,b,Aeq,beq,Vlb);
x,fval
%% 第二问:非线性规划
% 注意!第二问中求新料场位置,所以两个料场的横纵坐标也是变量,所以多了4个变量
% 对新坐标没有不等式约束,所以其不等式约束条件里的系数为0
A2 = [1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B2 = [20;20];
% 对新坐标也没有等式约束,所以相应项也为0
Aeq2 = [eye(6),eye(6),zeros(6,4)]; % 两个单位矩阵和一个全0矩阵拼成
beq2=[3 5 4 7 6 11]';
Vlb2=[zeros(12,1);-inf;-inf;-inf;-inf];
% 非线性规划必须赋初值,可以基于问题情况来设,或设置rand()随机数等等;
% 初始值设为线性规划的计算结果,即临时料场的坐标
% 设置初始值x0,此处可直接使用第一问的值作为初始值;
x0=[3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7]';
[x2,fval2]=fmincon(@fun2,x0,A2,B2,Aeq2,beq2,Vlb2)
% 若约束条件里有非线性函数,可使用在fmincon里使用nonlcon 项
% 若有条件,可使用蒙特卡罗法求一个近似解作为初始值
% 1、因为第2问模型中有16个变量,所以要给16个变量分别生成随机值,作为当前解;
% 2、判断这些当前解是否满足模型的约束条件
% 3、若满足,代入目标函数,求当前目标函数值
% 4、判断当前目标函数值是否比已求的较优函数值更好,若是,则替换掉较优函数值和对应的较优解
% 5、不断重复前5步,构成统计意义,求得较优解。
p0 = 10000; n = 10^6; tic
x_m0 = 0;
for i = 1:n
% 前12个数是6个工地从两个料场接收的量,6个工地分别需要3,5,4,7,6,11吨水泥
% 所以前12个变量分别需要取0到3,0到5,……,0到11的随机数
% 为加速求近似,取前12个变量(工地从料场接受的量)为随机整数
% randi(n)为随机取1到n之间的一个整数,则randi(n+1)-1为取0到n间随机整数
% 后4个变量是两个料场的横纵坐标,取一定范围内的随机数(根据题目,工地坐标都在0到9,所以此处取0到9)
% ...表示续行,即下一行和这行是在同一行
x_m = [randi(4)-1,randi(6)-1,randi(5)-1,randi(8)-1,randi(7)-1,randi(12)-1,...
randi(4)-1,randi(6)-1,randi(5)-1,randi(8)-1,randi(7)-1,randi(12)-1,...
9*rand(1,4)];
[g,k] = constraint(x_m); % 约束条件
if all(g<=0) % 等式约束难以严格满足,所以此处相差不大即可算近似
if all(abs(k)<=1)
ff = fun2(x_m); % 目标函数
if ff<p0
x_m0 = x_m; p0 = ff;
end
end
end
end
x_m0,p0,toc
% 以采样10^6次的蒙特卡罗法求得的近似值作为初始值,调用fmincon
[x3,fval3]=fmincon(@fun2,x_m0,A2,B2,Aeq2,beq2,Vlb2)
% 此时最终求得的结果fval3 = 85.4054,
% 优于前面以第一问线性规划结果为初始值时求得的90.4920
% 注意!!!非线性规划每次求解的结果都不一样!!!
% 多次运行相同代码,得出的结果不相同是正常的!!!
%% constraint.m
function [g,k] = constraint(x)
% 不等式约束条件
% sum(x(:,1:6),2)是对矩阵前6列按行求和,即对前6个元素求和,
% 对应6个工地接收第一个料场的总量。再减去20,即把不等式右边常数项移到左边
g = [sum(x(:,1:6),2)-20
sum(x(:,7:12),2)-20
];
% 等式约束条件,6个工地从两个料场收到的总量分别为3,5,4,7,6,11
k = [x(1)+x(7)-3
x(2)+x(8)-5
x(3)+x(9)-4
x(4)+x(10)-7
x(5)+x(11)-6
x(6)+x(12)-11
];
end
%% fun2.m
function ff = fun2(x)
% 6个工地坐标
a1 = [1.25 8.75 0.5 5.75 3 7.25];
b1 = [1.25 0.75 4.75 5 6.5 7.75];
f1=0;
% x(13)是第一个新料场的横坐标,x(14)是其纵坐标;
% x(15)是第二个新料场的横坐标,x(16)是其纵坐标;
for i=1:6
s(i)=sqrt((x(13)-a1(i))^2+(x(14)-b1(i))^2); % 第一个料场到各工地的距离
f1=s(i)*x(i)+f1; % 第一个料场给各工地的吨千米数
end
f2=0;
for i=7:12
s(i)=sqrt((x(15)-a1(i-6))^2+(x(16)-b1(i-6))^2); % 第二个料场到各工地的距离
f2=s(i)*x(i)+f2; % 第二个料场给各工地的吨千米数
end
% 总运输量(吨千米数)
ff=f1+f2;
end
2 python
4 整数规划和0-1规划
- 在整数规划中,如果所有变量都限制为整数,则称为纯整数规划;
- 如果仅一部分变量限制为整数,则称为混合整数规划。
- 整数规划的一种特殊情形是0-1规划,它的变数仅限于0或1。
1 matlab
2 python
5 最大最小化规划模型 ( Minimax )
- 最大最小化:最小化最坏情况
- 最大最小算法(Minimax算法),是一种找出失败的最大可能性中的最小值的算法(即最小化对手的最大得益)。在实际问题中也有许多求最大值的最小化问题,例如急救中心选址问题就是要规划其到所有地点最大距离的最小值,在投资规划中要确定最大风险的最低限度等,为此,对每个
matlab
python
6 多目标规划模型
- 多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。
- 设计一个导弹,既要射程远,命中率高,还要耗燃料少
- 选择新厂址,除了要考虑运费、造价、燃料供应费等经济指标外,还要考虑对环境的污染等社会因素
- 解题思路
- 把目标函数转换成约束条件,多目标转换为单目标
- 本节内容
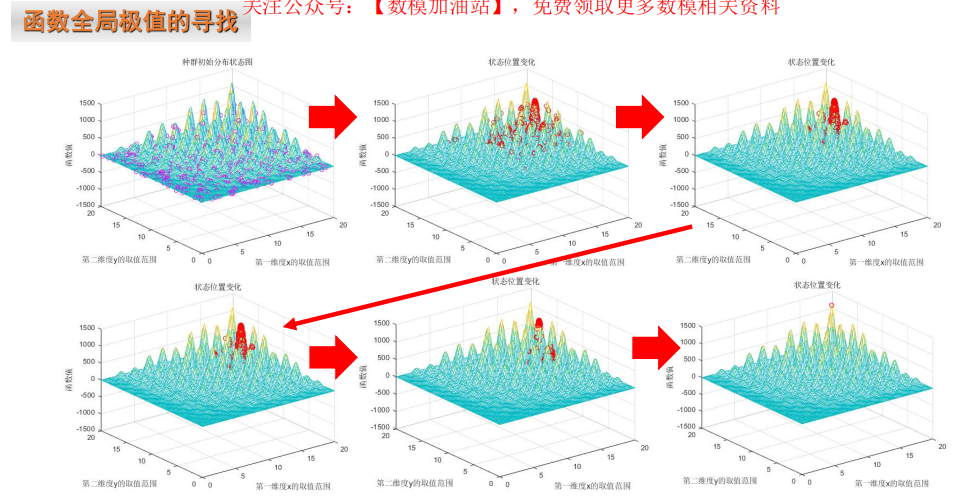
7 智能优化算法
智能优化算法又称为现代启发式算法,是一种具有全局优化性能、通用性强、且适合于并行处理的算法。这种算法一般具有严密的理论依据,而不是单纯凭借专家经验,理论上可以在一定的时间内找到最优解或近似最优解。
特点:都是从任一解出发,按照某种机制,以一定的概率在整个求解空间中探索最优解。由于它们可以把搜索空间扩展到整个问题空间,因而具有全局优化性能。
7.1 粒子群算法 ( PSO )(有代码)
3 原理
原理描述
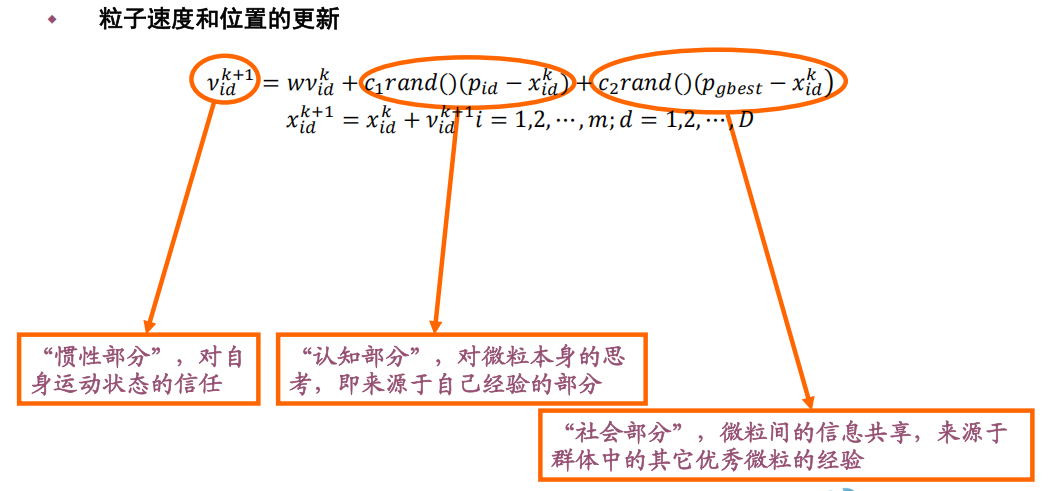
- 初始化为一群随机粒子,通过迭代找到最优。
- 每次迭代中,粒子通过跟踪“个体极值(pbest)”和“全局极值(gbest)”来 更新自己的位置。
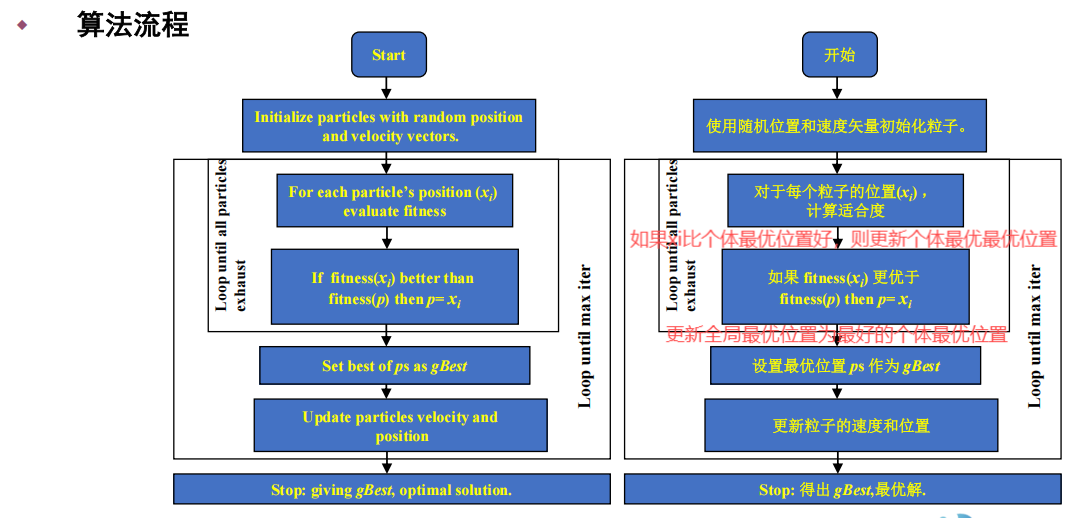
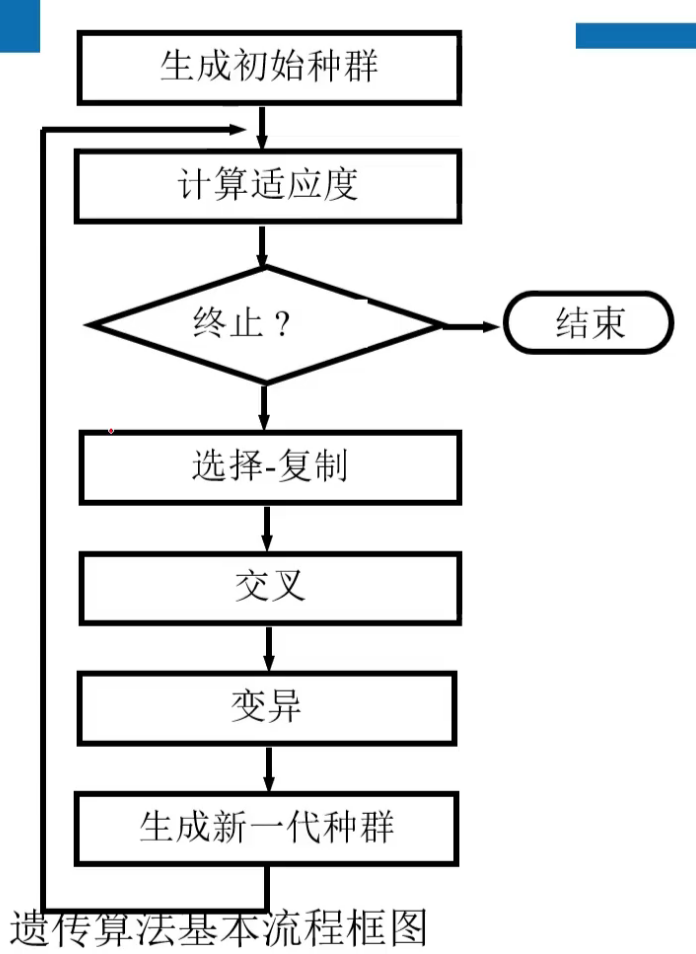
算法
算法流程
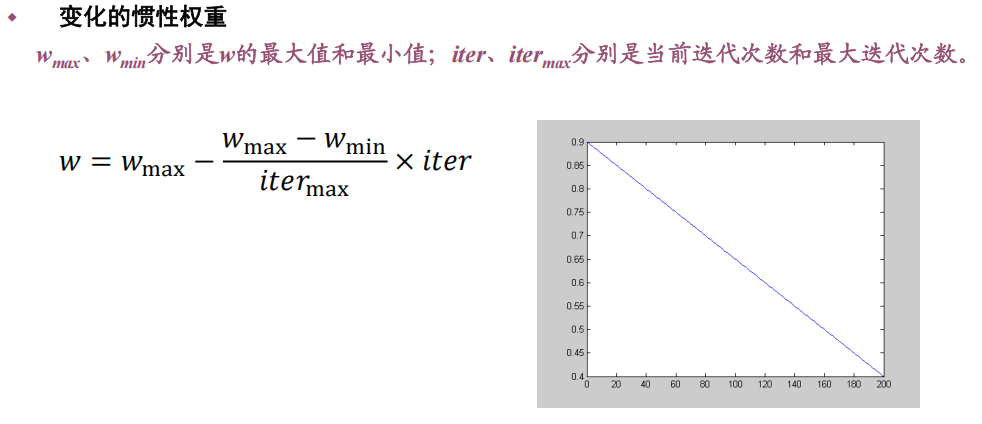
4 参数分析
pro版
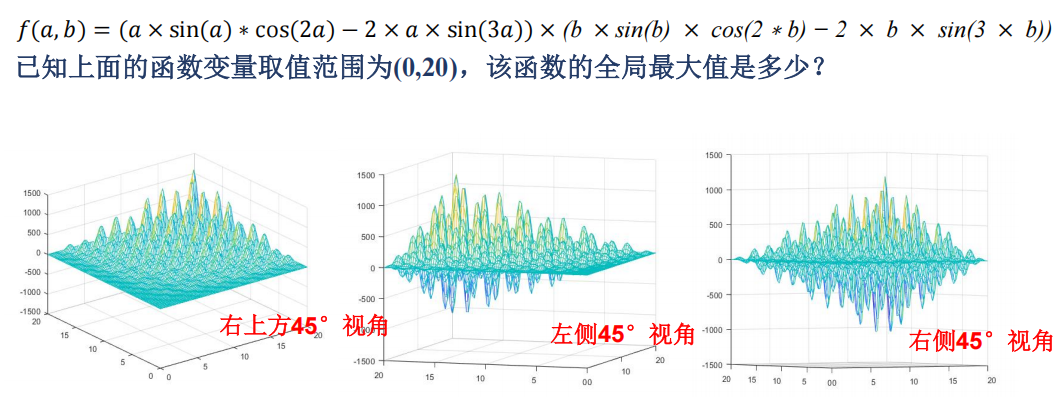
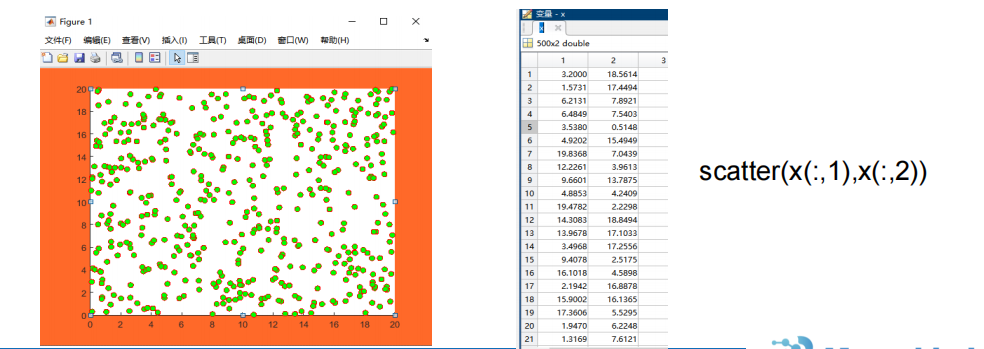
5 算法实现(有代码)
6 群智能优化的特点和不足
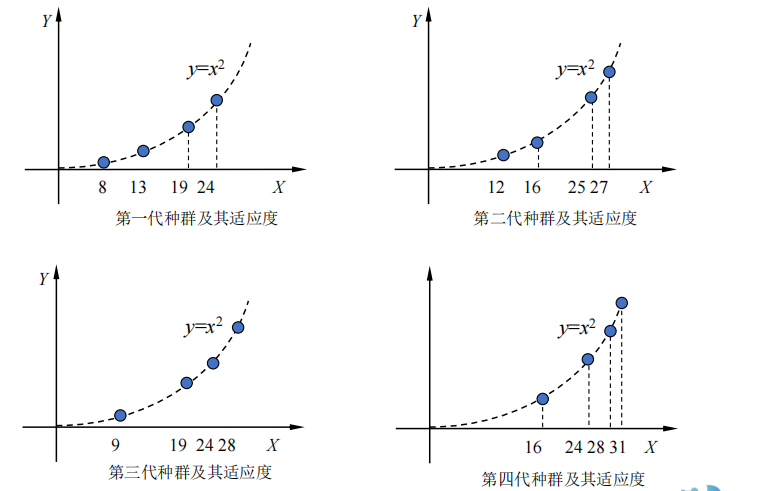
7.2 遗传算法(用工具箱)
1 算法原理
- 染色体与基因
- 遗传操作
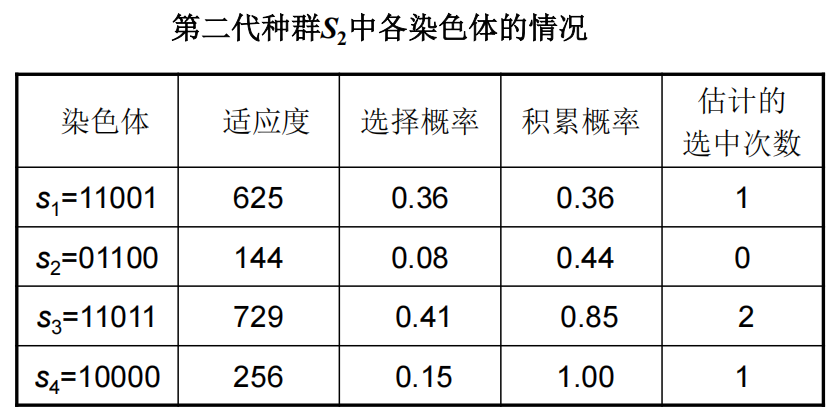
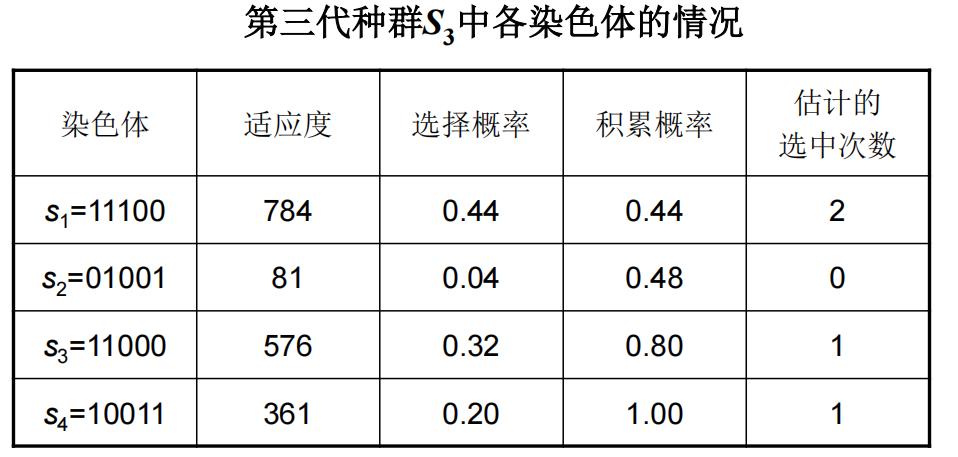
- 选择-复制
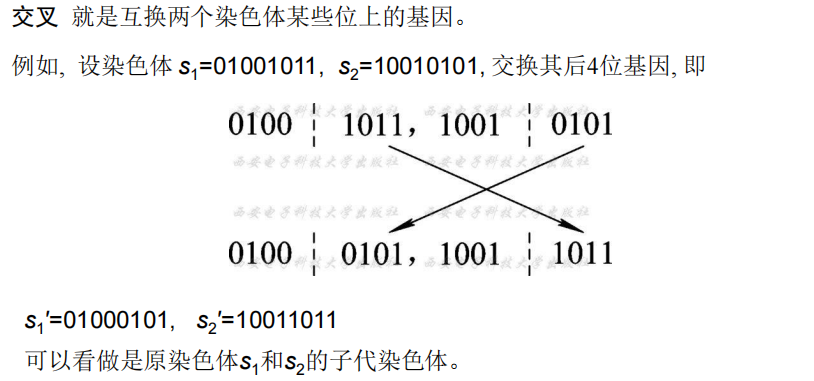
- 交叉
- 变异
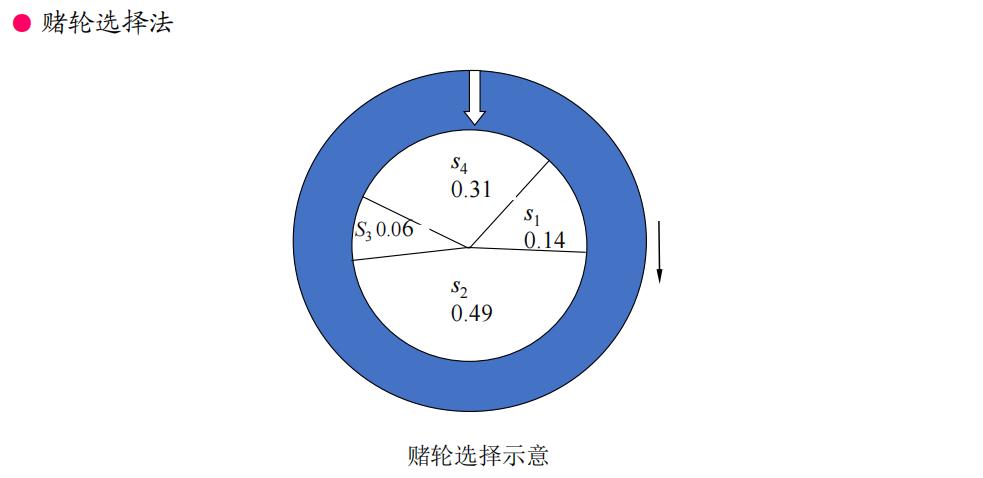
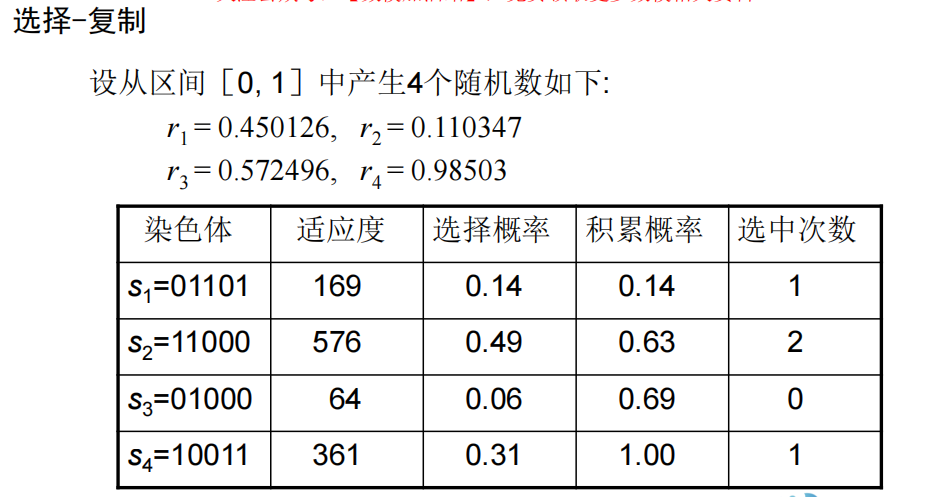
- 选择-复制
算法流程
2 算法分析
3 算法实现
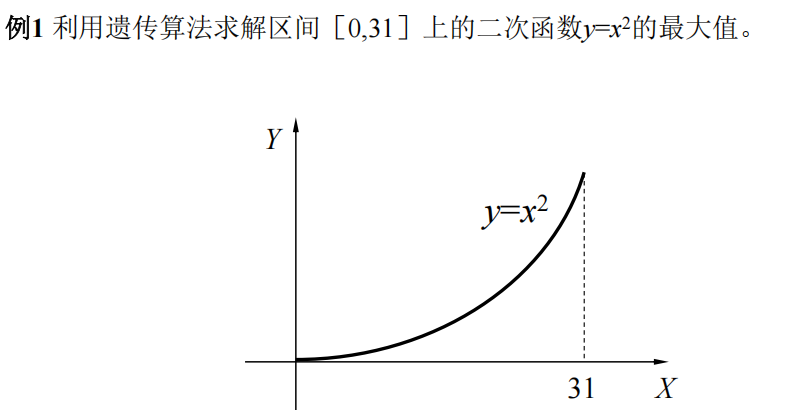
例1
总结
遗传算法的主要特点
- 遗传算法一般是直接在解空间搜索, 而不像图搜索那样一般是在问题空间搜索, 最后才找到解。
- 遗传算法的搜索随机地始于搜索空间的一个点集, 而不像图搜索那样固定地始于搜索空间的初始节点或终止节点, 所以遗传算法是一种随机搜索算法。
- 遗传算法总是在寻找优解, 而不像图搜索那样并非总是要求优解, 而一般是设法尽快找到解, 所以遗传算法又是一种优化搜索算法
- 遗传算法的搜索过程是从空间的一个点集(种群)到另一个点集(种群) 的搜索,而不像图搜索那样一般是从空间的一个点到另一个点地搜索。 因而它实际是一种并行搜索, 适合大规模并行计算,而且这种种群到种群的搜索有能力跳出局部最优解。
- 遗传算法的适应性强, 除需知适应度函数外, 几乎不需要其他的先验知识。
- 遗传算法长于全局搜索, 它不受搜索空间的限制性假设的约束,不要求连续性, 能以很大的概率从离散的、多极值的、 含有噪声的高维问题中找到全局最优解。
遗传算法的应用
- 遗传算法在人工智能的众多领域便得到了广泛应用。例如,机器学习、聚类、控制(如煤气管道控制)、规划(如生产任务规划)、设计(如通信网络设计、布局设计)、调度(如作业车间调度、机器调度、运输问题)、配置(机器配置、分配问题)、组合优化(如TSP、背包问题)、函数的最大值以及图像处理和信号处理等等。
- 另一方面,人们又将遗传算法与其他智能算法和技术相结合,使其问题求解能力得到进一步扩展和提高。例如,将遗传算法与模糊技术、神经网络相结合,已取得了不少成果。
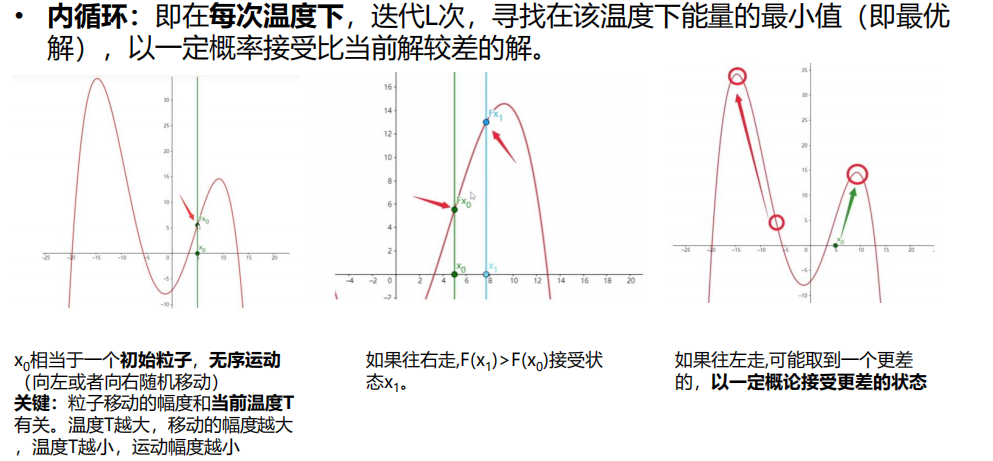
7.3 模拟退火算法(有代码)
2 算法原理
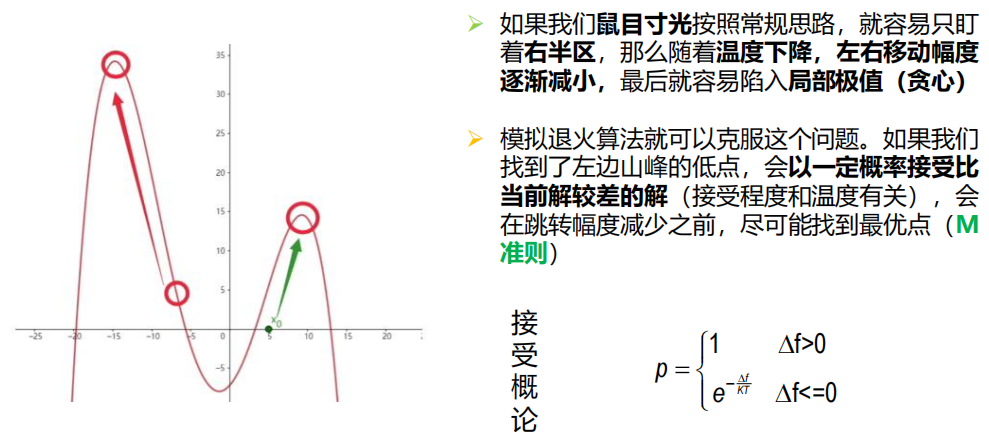
原理
3 算法流程
4 算法特点
5 算法拓展
7.4 天牛须搜索(有代码)
3 算法原理
4 算法特点
- 优点
- 运算量非常小,收敛非常快
- 具有全局寻优能力
- 代码非常简洁,容易实现
- 缺点
- 有可能陷入局部最小值
- 步长的选取需要根据实际情况确定
- 迭代次数增加导致寻优步长过小
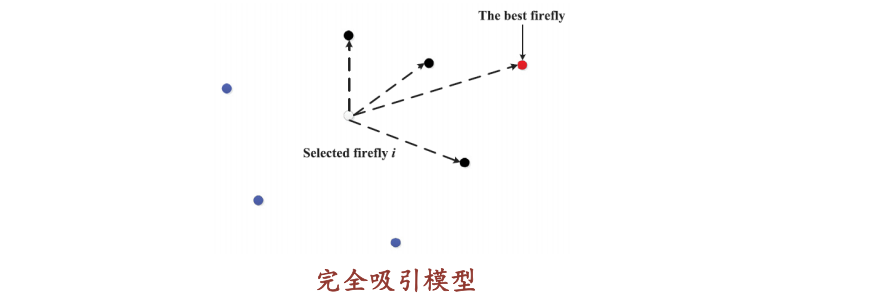
7.5 萤火虫算法(有代码)
2 算法原理
算法原理
算法步骤
伪代码
3 算法改进
APFA 参数自适应策略
CFA 混沌映射策略
- 高斯映射
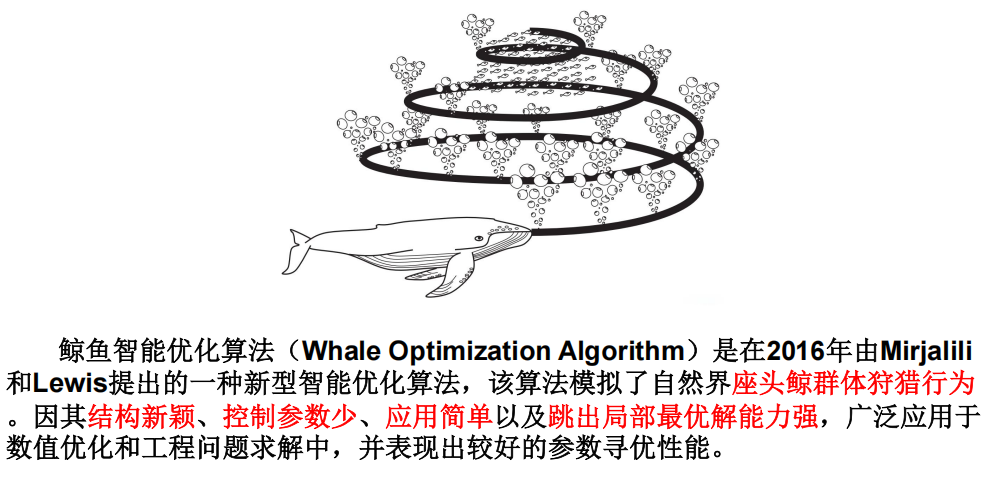
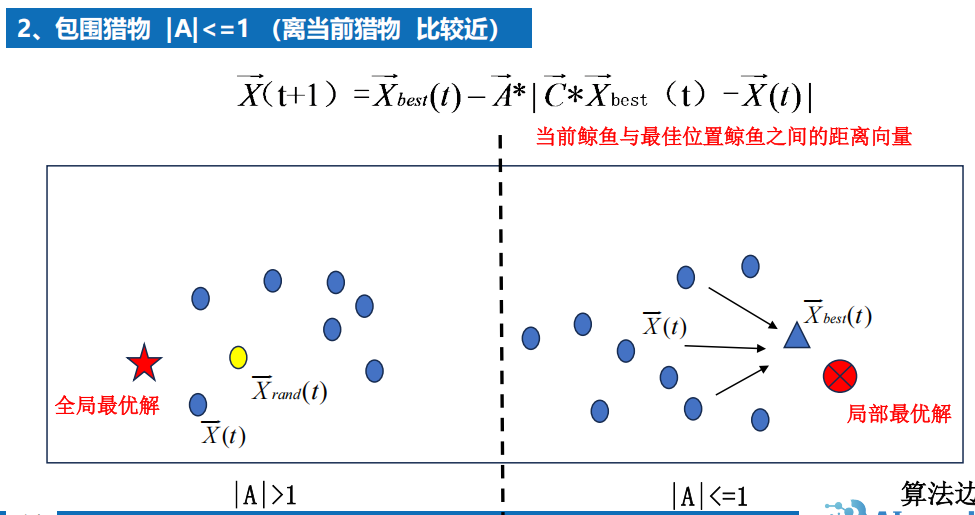
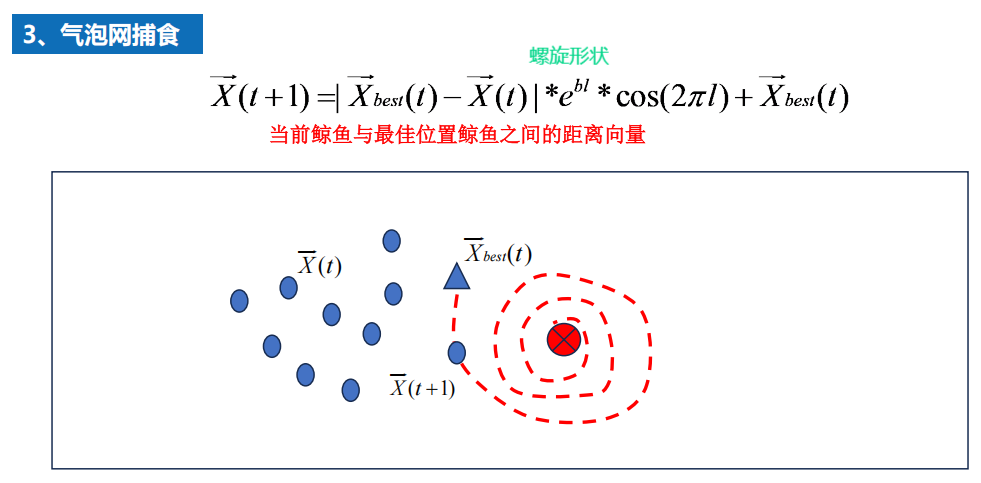
7.6 鲸鱼优化算法(有代码)效果不好???
1 背景
2 算法
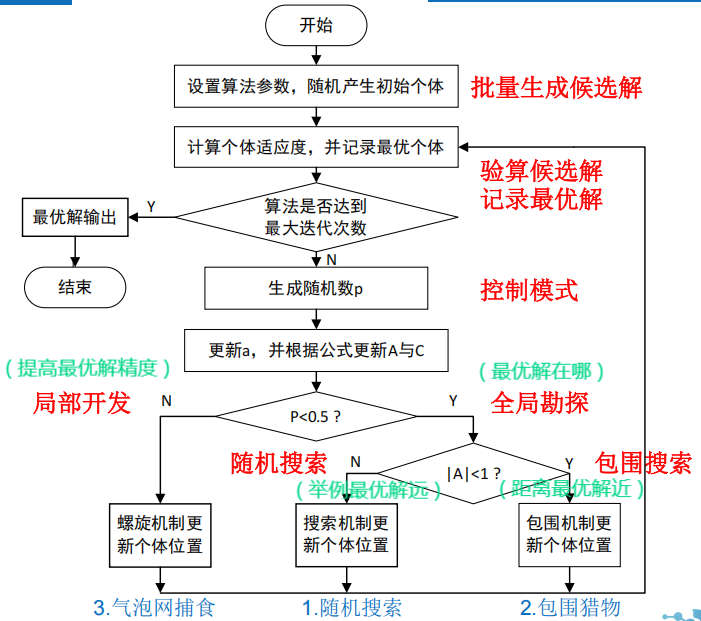
流程图
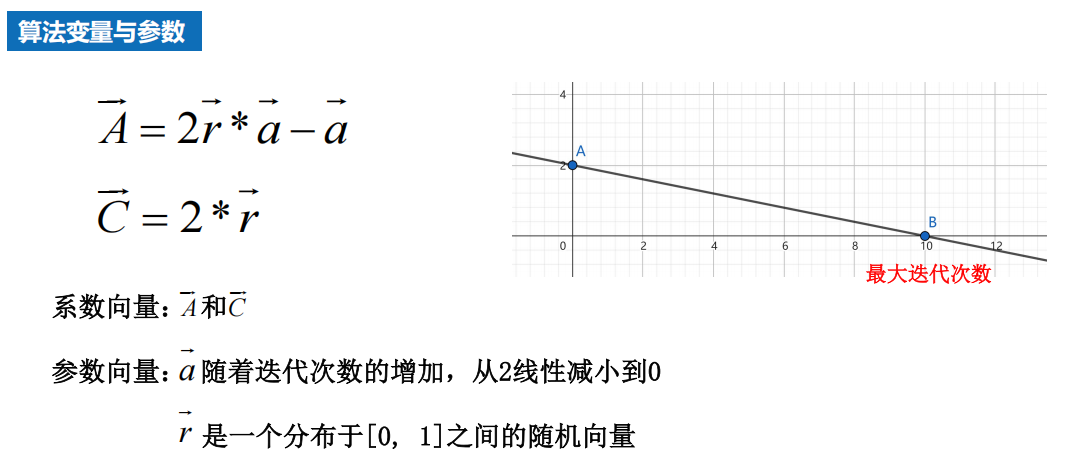
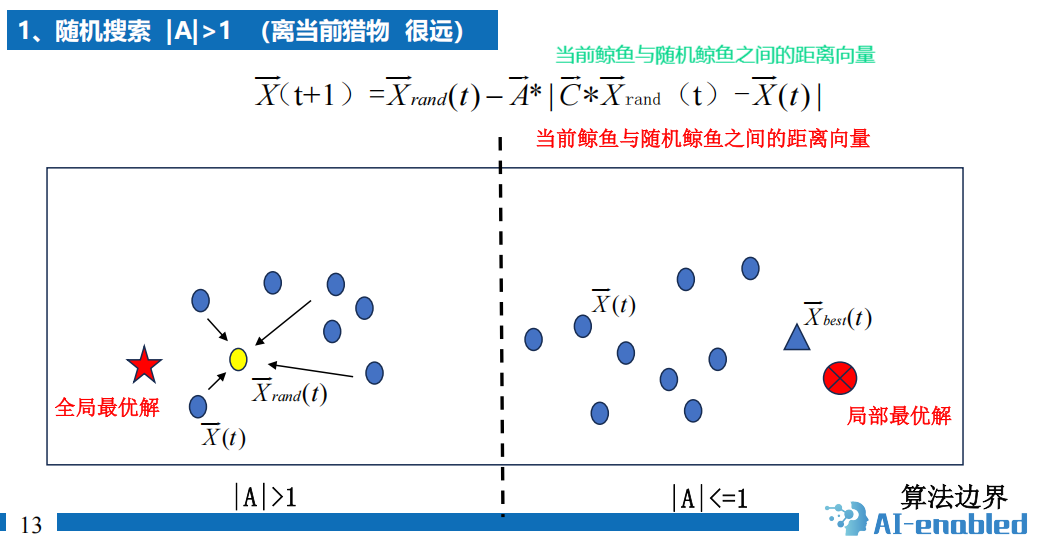
原理
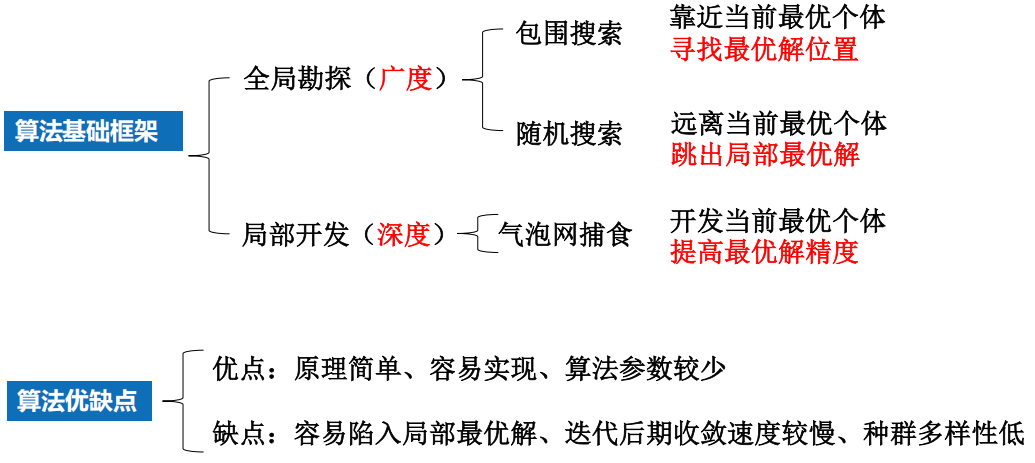
3 算法分析
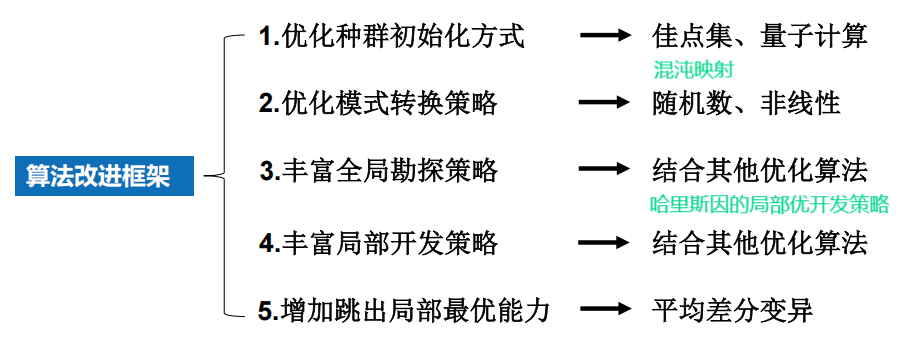
4 算法拓展