12.1 树的一般定义
-
树:连通且无圈的无向图称为树。
-
林:无圈的无向图称为林。林是每个连通分支都是树的无向图。
-
树的等价定义
设
-
树叶、分支顶点:称树中次数是 1 的顶点为树叶,次数大于 1 的顶点为分支顶点
-
定理12.3:非平凡树中至少有两片树叶
12.2 根数与有序树
-
有向树:若不考虑弧的方向,有向图 D 成为树,则称 D 为有向树。或者说,将一个树的边加上任意的方向,就得到有向树。任何有向树都是弱连通的无回路有向图,但是弱连通的无回路有向图未必是有向树(如下图)。
-
树根、根数:若有向树 T 有一个顶点的引入次数为0,其余顶点的引入次数都为 1,则称 T 为根树。称根树中引入次数为 0 的顶点为树根。
-
树叶、分支顶点、级:在根树中,称引出次数为 0 的顶点为树叶,称既不是树根也不是树叶的顶点为分支顶点。从树根到一个顶点的通路的长度称为该顶点的级。
-
树高:在根树中,所有通路都是基本通路,从树根到每个顶点有唯一的通路。树根的级为 0。根树中顶点的级的最大值称为树高
-
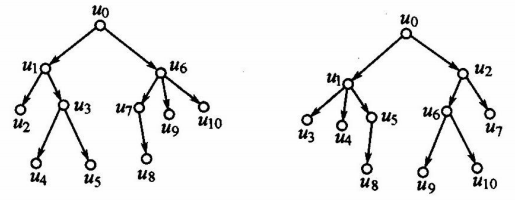
有序树:称为顶点或弧指定了次序的根树是有序树。若从顶点 u 可以到达 v ,则称 v 为 u 的后裔, u 为 v 的祖先。若 < u, v > 是弧,则称 v 为 u 的儿子,u为 v 的父亲,同一顶点的儿子互为兄弟。
作为根树,以上两树是一样的,作为有序树,它们是不同的
12.3 二元树
- m元树、完全m元树、位置m元树
- 每个顶点的引出次数都小于等于 m 的根树称为 m 元树。
- 每个顶点的引出次数都等于 m 或 0 的根树称为完全 m 元树。
- 若为 m元树 T 中每个顶点的各儿子规定了位置,则称 T 为位置 m 元树。
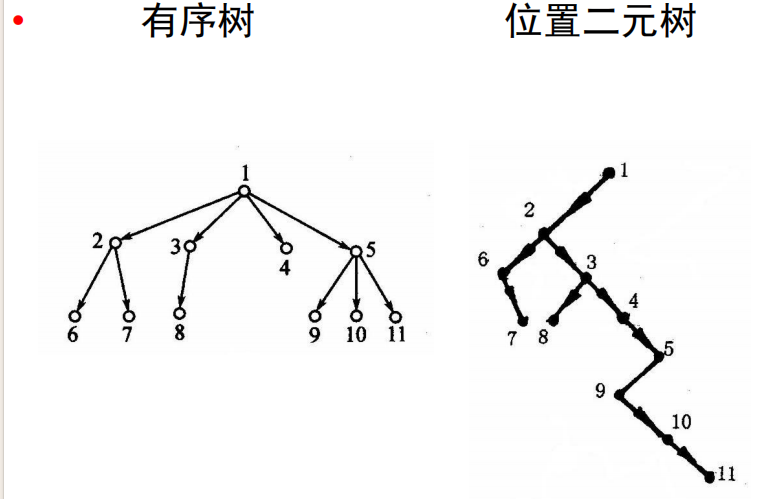
有序树转换为位置二元树的算法
-
若 u 是原来有序树的树根,则它仍然是转换后的位置二元树的树根。
-
在原来有序树中,
- 若顶点 u 是 v 的大儿子,则在转换后的位置二元树中,u 是 v 的左儿子;
- 若顶点 u 是 v 的大兄弟,则在转换后的位置二元树中,u 是 v 的右儿子。
-
每个弱分图都是有序树,并且为各有序树规定了顺序的有向图称为有序林。如果称排在前面的有序树的树根是排在后面的有序树的树根的哥哥,并规定转换后的位置二元树的树根是有序林中第一个有序树的树根,则可按照上面的算法将有序林转换为位置二元树。
前缀码
-
若存在非空符号串
例如,{00, 10, 11} 是二元前缀码, {1, 00, 10, 11} 不是二元前缀码 -
二元树和二元前缀码
让位置二元树中的每个顶点对应一个 {0, 1} 上的字,令所有树叶对应的字的集合为该位置二元树产生的二元前缀码。- 顶点对应的字归纳定义如下:
- 树根对应空字
- 若顶点 u 对应字
, 的 右 儿 子 对 应
- 树根对应空字
- 每个顶点对应字的长度等于该顶点的级。从顶点 u 可以到达另一顶点 v 当且仅当 u 对应的字是 v 对应的字的前缀。因为从一个树叶不可能到达另一树叶,所以位置二元树产生的语言是二元前缀码。反之,任意二元前缀码都可由一个位置二元树产生。
- 顶点对应的字归纳定义如下:
最优二元树
-
设位置二元树
-
在所有带权为
-
设 t ≥ 2, P1 ≤ P2 ≤ … ≤ Pt ,则存在一个带权P1 ,…, Pt 的最优二元树使得权为 P1 和 P2 的树叶是兄弟。
-
设 t ≥ 2, P1 ≤ P2 ≤ … ≤ Pt ,T 是带权P1 + P2 , P3 , … , Pt 的二元树。为 T 中带权P1 + P2 的树叶增加两个分别带权 P1 , P2 的儿子得到带权 P1 , … , Pt 的二元树 T' 。那么, T 是带权P1 + P2 , P3 , … , Pt 的最优二元树当且仅当 T' 是带权P1 , P2 , … , Pt 的最优二元树
-
Huffman算法
12.4 生成树
-
若无向图 G 的生成子图 T 是树,则称 T为 G 的生成树。
-
设 T 是无向图 G 的生成树。称 T 中的边为 T 的树枝,称 G 的不在 T 中的边为 T 的弦,弦的集合称为 T 的补。(n, m) 无向图 G 的任何生成树有 n − 1 个树枝,m − n + 1 条弦。当然, G 的某条边可能是这棵生成树的树枝,却是另一棵生成树的弦
-
定理12.7:无向图 G 有生成树当且仅当它是连通的。
-
基本圈、基本圈组:(n, m) 无向图 G 的生成树 T 有 m − n + 1 条弦。任取 T 的一条弦 e , T + e 有唯一的圈,它由树枝和弦e 组成,称这样的圈为对应于弦 e 的基本圈。由这 m− n + 1 个基本圈组成的集合称为关于生成树 T 的基本圈组。
最小生成树
设 G 是带权连通无向图,其中每条边 e 的权C(e) 是正实数。G 的生成树 T 的各边权值之和称为 T 的权,记为 C(T) 。
- 设 G 是带权连通无向图。在 G 的生成树中,权值最小的树称为 G 的最小生成树
12.5 割集
-
割集(最小的 能把图分成两块的边的集合):设连通无向图
割集的等价定义: -
桥:
-
基本割集(一个树枝一堆弦)、基本割集组:设
-
定理12.8:每个圈与任何生成树的补(即弦的集合)至少有一条公共边,即每个圈中都包含弦。
-
定理12.9:每个割集与任何生成树至少有一条公共边,即每个割集中都包含树枝。
-
定理12.10:任何圈和任何割集都有偶数条(包含零条)公共边。
-
定理12.11:给定图
-
定理12.12:给定图