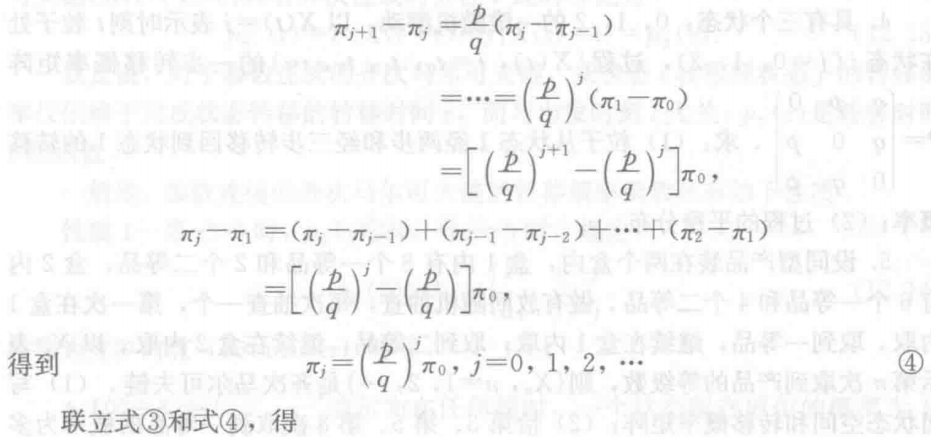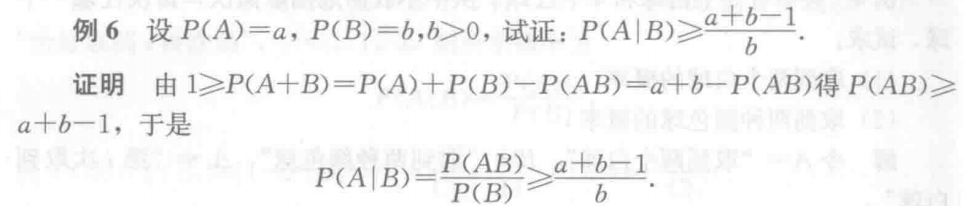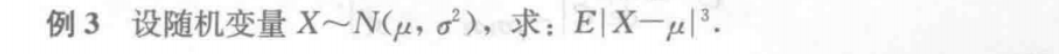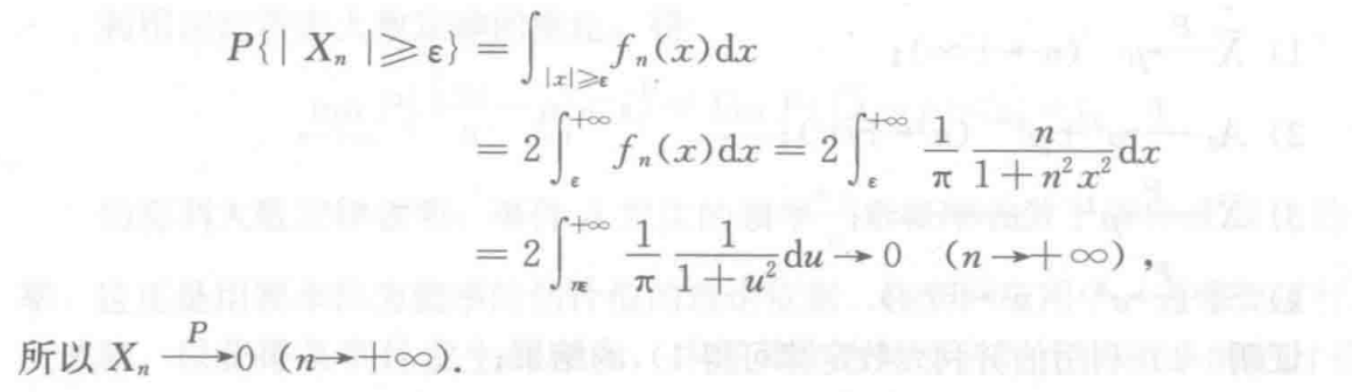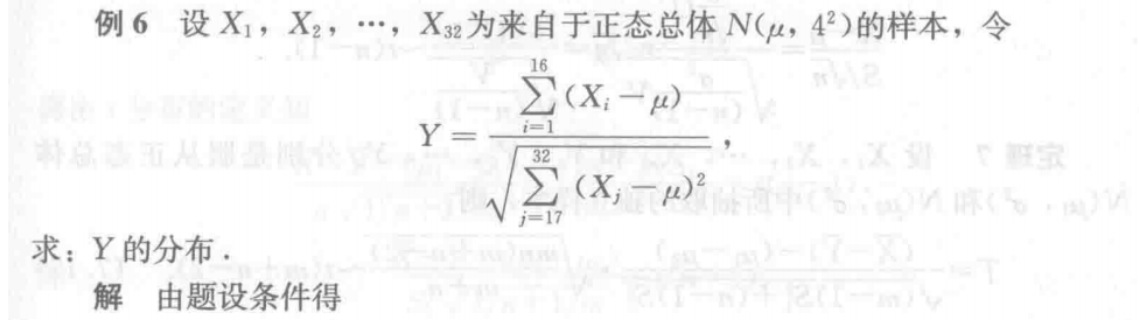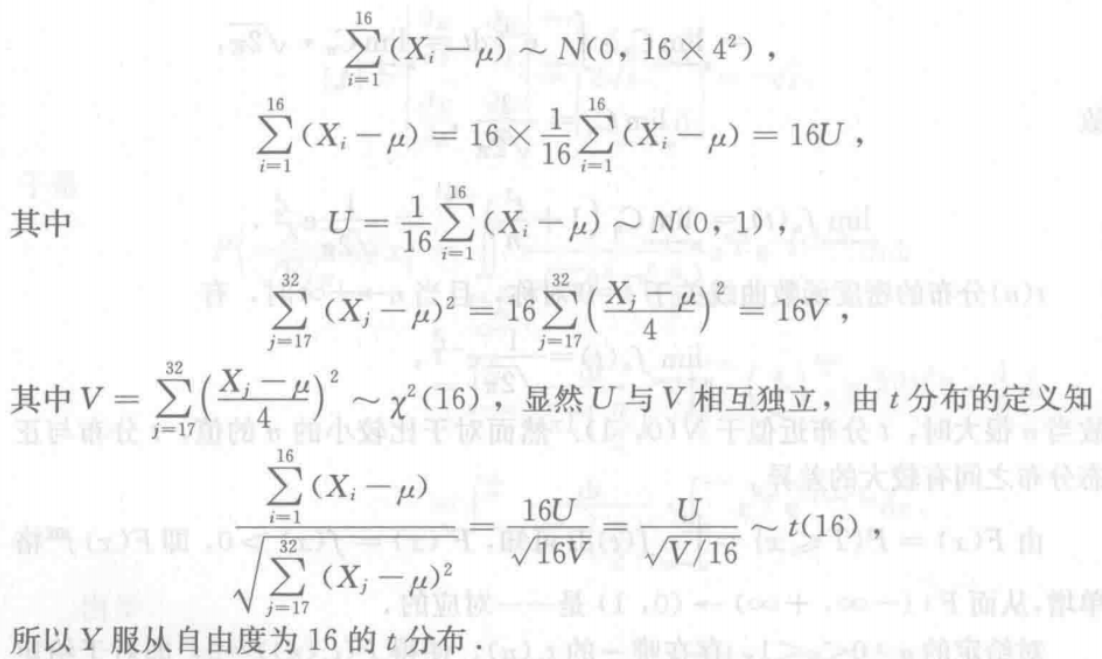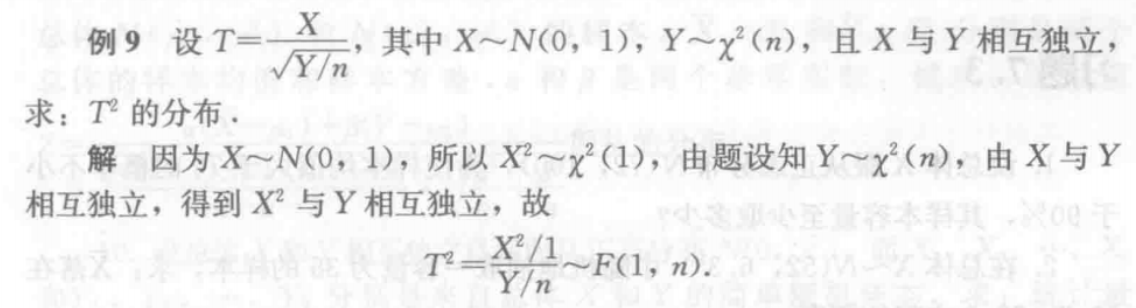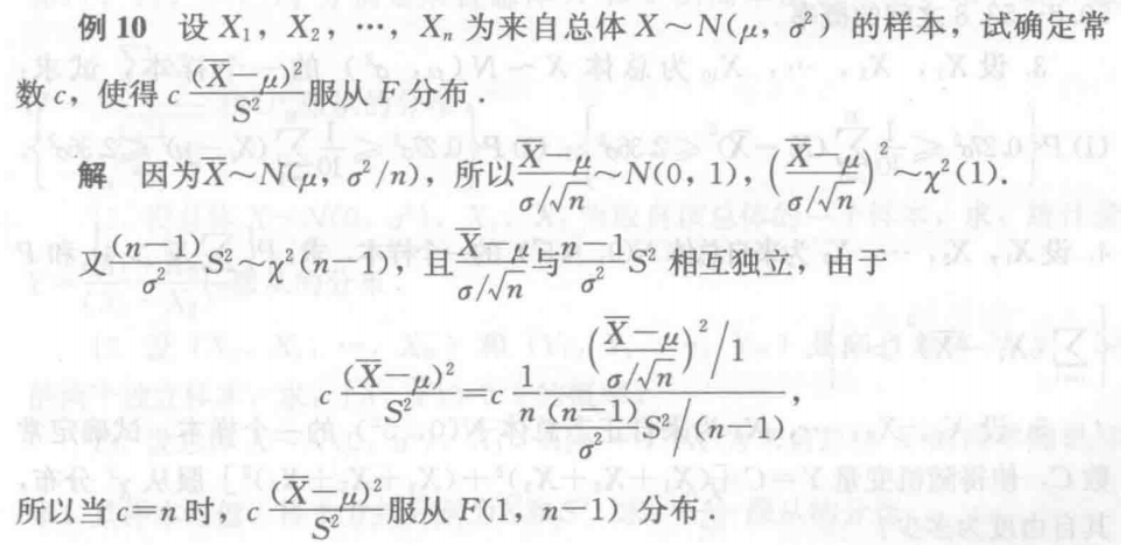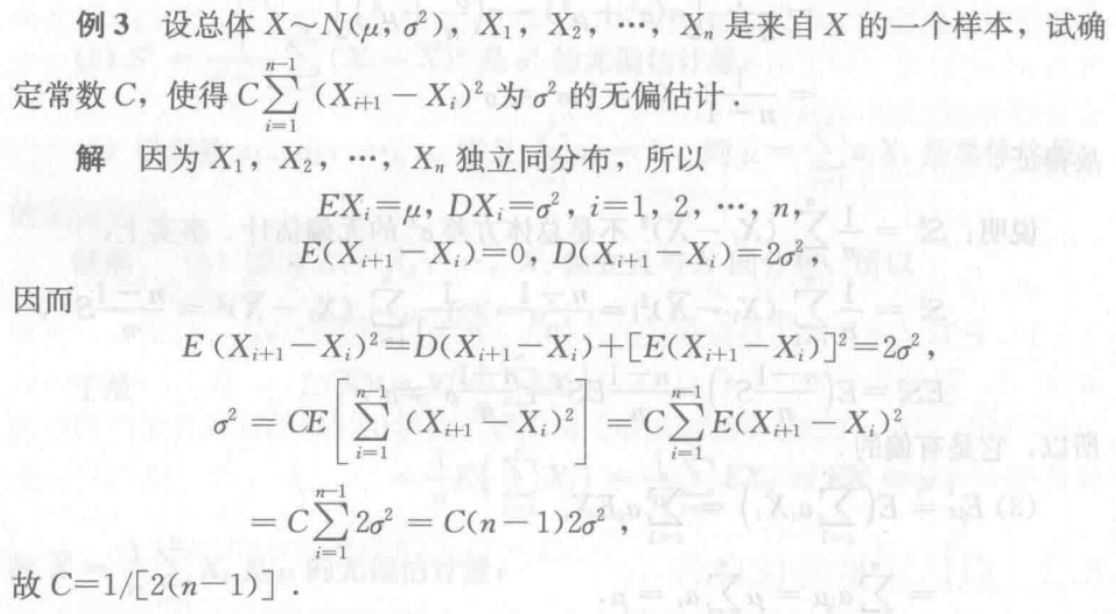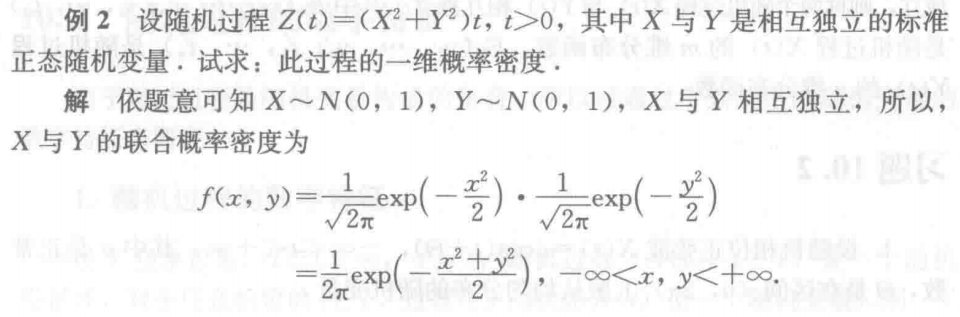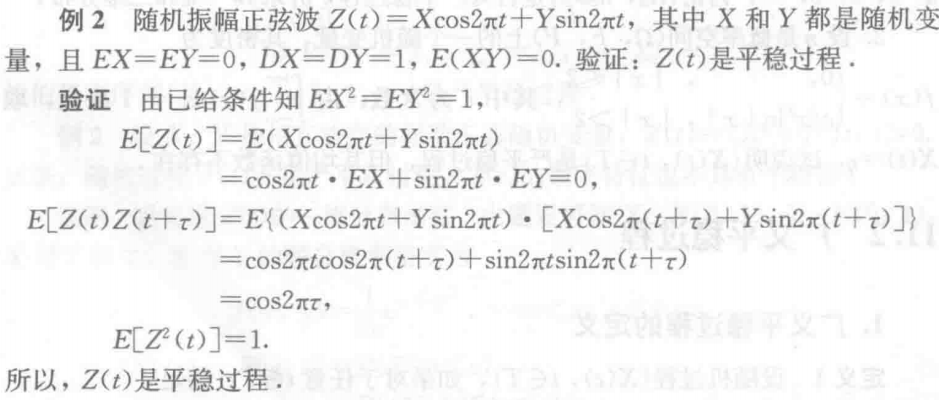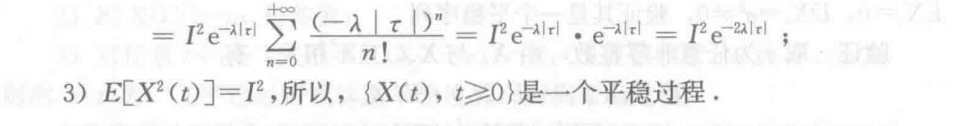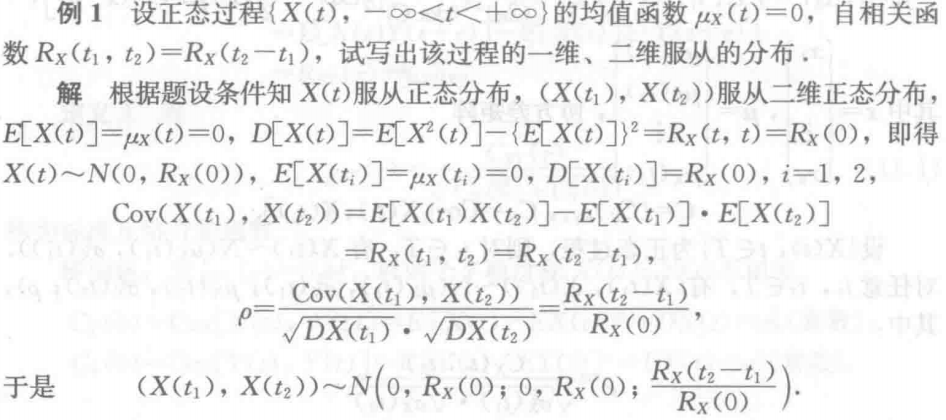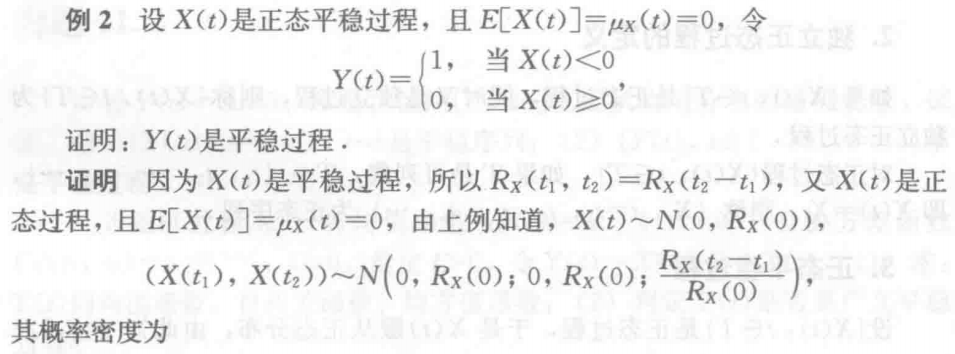概率论
第1章 概率模型 笔记01
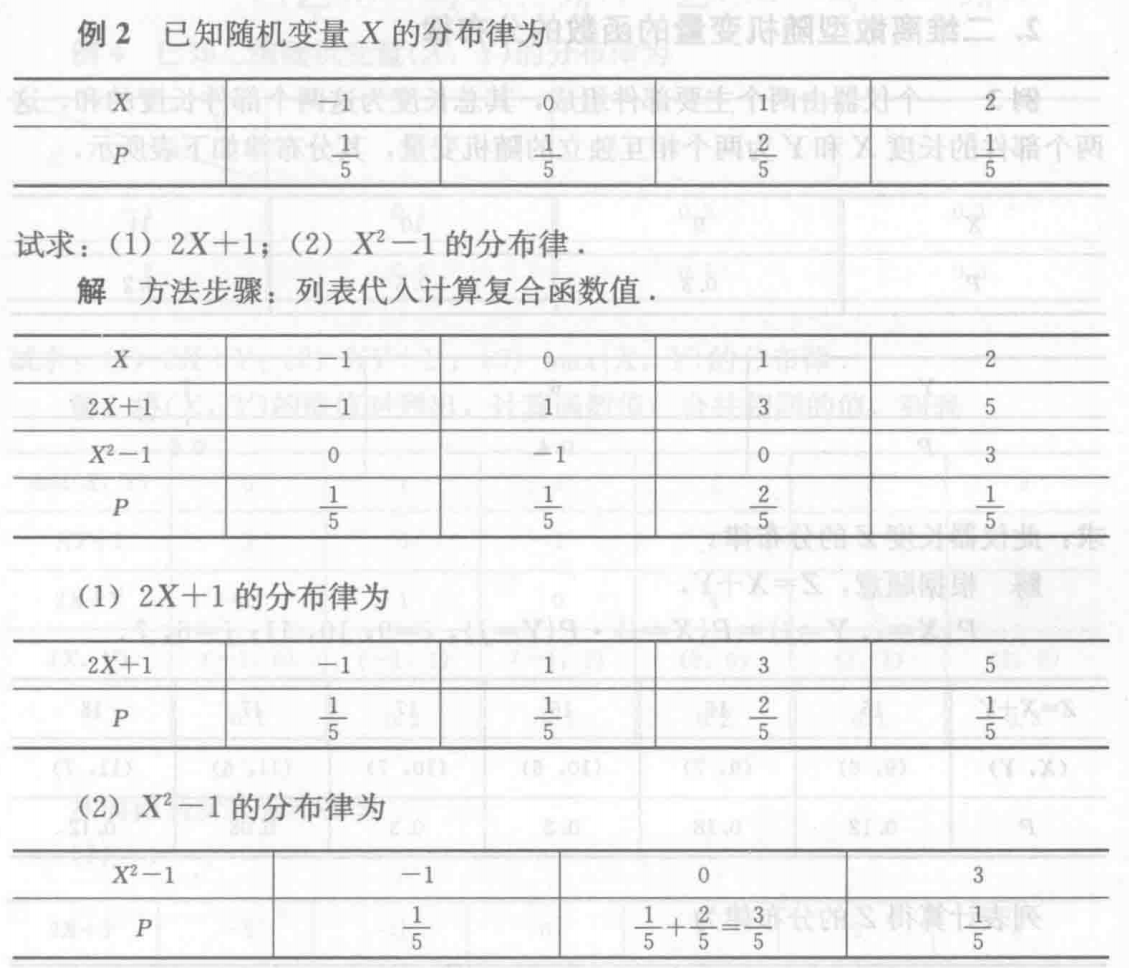
1.0 例题们
事件相容5.2
几何概率12.6
古典概率19.2
加法公式、乘法公式24.6
全概率公式26.2
独立事件34.7
1.1 随机事件与样本空间(事件相容与互逆)
1.1.1 试验
- 确定性实验或必然试验
- 随机试验(简称试验):用字母
- 在相同条件下可以重复进行
- 每次实验的结果不止一个,但能事先明确可能出现的结果范围
- 每次试验之前不能准确预言哪个结果会出现
1.1.2 随机事件
- 随机事件(简称事件)
- 在试验中可能发生也可能不发生的结果
- 用字母
- 基本事件:试验中每一个可能的结果,是最简单的随机事件
- 常用小写字母
- 随机事件是由若干个基本事件组成的
- 随机事件发生
- 常用小写字母
- 必然事件:在试验中必然发生的事件,记为
- 不可能事件:不可能发生的事件,记为
(必然事件和不可能事件不是随机事件,当作特殊的随机事件)
1.1.3 样本空间(集合论)
- 定义:试验的全部基本事件组合成的集合,称为试验的样本空间,记为
- 试验的基本事件:是样本空间的元素(样本点)
- 随机事件是样本空间的子集
- 不可能事件表示空集,必然事件表示样本空间
- 完备事件组:若
1.1.4 随机事件的关系(事件相容与互逆)(集合论)
随机事件的关系:
- 包含:
- 相等:
- 并(和):
- 交(积):
- 事件的互不相容(互斥):
- 事件的互逆(相互对立):
- 称
- 称
- 事件的差:
运算律:
- 吸收律
- 分配律
- 反演律(De Morgan 公式)
- 和事件分解为互不相容事件的和
- 差化积
- 重余律
- 幂等律
- 交换律
- 结合律
1.2 概率的定义及性质(排列组合)
对于事件
- 表示事件
- 是事件
则称
1.2.1 古典概率(排列组合)
- 定义:
- 样本空间
- 每个基本事件发生的可能性相等,即
则称这种试验为古典型随机试验,简称古典概型。
- 样本空间
- 排列数记号:
- 组合数记号:
- 乘法原理
- 古典概率的性质:
- 对任意随机事件
- (有限可加性)若事件
- 对任意随机事件
1.2.2 几何概率
- 定义:设几何概型的样本空间为
- 性质:
- 对任一随机事件
- (有限可加性)若事件
- (可列可加性)若事件
- 对任一随机事件
1.2.3 概率的统计定义
- 频率的定义:设某实验重复做了
- 频率的性质
- 对任一随机事件
- 若事件
- 对任一随机事件
- 统计概率的定义:若随着试验次数
- 概率的近似求法:
1.3 概率的公理化定义(加法公式)
1.3.1 事件域
随机试验
, - 若
- 对任意有限个或可列个
也就是说,
1.3.2 概率的公理化定义
设
- 对每一个
, - 对任意可列个互不相容的事件
则称
1.3.3 概率的性质
- 不可能事件的概率为0,即
- 概率具有有限可加性
- 对任意事件
- 若
- 加法公式:对任意事件
1.4 条件概率与乘法公式
- 定义:
- 性质
- 若
- 对任意事件
- 乘法公式:
- 当
1.5 全概率公式与贝叶斯公式
设事件组
全概率公式:
则对任意事件
贝叶斯公式:
对任意事件
1.6 事件的独立性
1.6.1 两个事件的独立性
定义:
对任意两个事件
则称
定理:
对任意事件
性质:
概率为
- 概率为
- 概率为
1.6.2 多个事件的独立性
定义:
- 若事件
- 若事件
1.6.3 独立事件的性质
若
(可推广到多个事件)
第23章 随机变量与随机向量 笔记02的1 2
给出离散情形的分布函数,可以画表格或者写F
2.0 例题们
分布函数的性质
离散型随机变量、分布列、分布函数
二项分布
连续随机变量 已知概率密度求分布、求P
连续分布
正态分布 分位点
2.1 随机变量
定义:
设随机试验
2.2 随机变量的分布函数
2.2.1 定义:
设
记为
2.2.2 性质:
-
取值范围:
-
单调不减:
-
右连续:
反之:若定义在 -
对任意实数
-
对任意实数
2.3 离散型随机变量及其概率分布
2.3.1 离散型随机变量的定义
若随机变量
2.3.2 离散型随机变量分布律的表示方法
- 公式法
- 列表法或矩阵法
| … | … | ||||
|---|---|---|---|---|---|
| … | … |
2.3.3 离散型随机变量的分布律的性质
2.3.4 定理
设离散型随机变量
- 对于任意区间
- 由分布函数可确定分布律
2.4 常用离散型随机变量的分布(几何分布)
2.4.1 两点分布
定义:
若随机变量
则称
2.4.2 二项分布
来源:
重伯努利试验
设试验只有两个可能的结果: 和 。
将试验独立地重复做 次,则这 次独立重复试验称为 重伯努利试验。
如果随机变量
则称
两点分布是二项分布的特殊形式
2.4.3 泊松分布
定义:
若随机变量
则称
泊松分布适用于描述单位时间(或空间)内随机事件发生的次数。
Poisson 定理
设
Poisson 定理说明:若
2.4.4 几何分布(Geom(p))
- 随机变量
- 概率模型:重复试验直到首次成功时的试验次数。
- 应用:离散等待时间和无记忆性
2.4.5 超几何分布
设一批产品中有
这个分布称为超几何分布,记为
2.5 连续型随机变量及其概率密度函数
2.5.1 定义
设随机变量
则称
2.5.2 概率密度函数的性质
-
对一切
-
反之,任何一个具有以上性质的可积实函数 -
连续型随机变量取任何特定值的概率都是 -
设
连续性随机变量在任一区间上取值的概率为此区间上概率密度函数曲线下方的曲边梯形的面积。
设
- 若
- 若
2.6 常用的连续型随机变量分布(正态分布)
2.6.1 均匀分布
若连续型随机变量
则称
2.6.2 指数分布
如果随机变量
则称
若
2.6.3 正态分布
定义:
若
其中
性质:
- 曲线关于直线
- 曲线在
2.6.4 标准正态分布
参数
即
标准正态分布
定义:
设
称
分位点的性质:
3.0 例题们
分布函数
二维离散变量 联合分布律
二维离散变量 联合分布律 边缘分布律
二维连续变量 边缘概率密度
二维连续变量 条件概率密度
二维离散变量 边缘分布律 独立
3.1 二维随机变量
3.1.1 定义1
设试验
3.1.2 定义2
设
分布函数
- 定义域:
- 取值范围:
- 特殊值:
- 对任意实数
3.1.3 定义3
设试验
设
3.2 二维离散型随机变量
3.2.1 定义
若二维随机变量
3.2.2 分布律
记
称为二维离散型随机变量
分布律的表示法:(1)公式法;(2)列表法
3.2.3 性质
3.2.4 定理
设
则随机点
其中和式是对所有使
3.3 二维连续型随机变量
3.3.1 定义
设二维随机变量
则称
3.3.2 性质
反之, 若二元函数- 如果概率密度
3.2.3 用概率密度计算概率
定理:设
- 设
3.2.4 常用的二维连续型随机变量有下面几种:
均匀分布
若二维连续型随机变量
其中
二维正态分布
若随机变量
其中
3.3 边缘分布函数
定义:
设二维随机变量
分量
称
分量
称
注:
已知联合分布函数
但由
3.3.1 边沿分布律
定义:
二维离散型随机变量
边沿分布律的计算:
3.3.2 条件分布律
在已知一个分量取某一定值的条件下,另一个分量的分布律称为条件分布律。
定义
设二维离散型随机变量
(1) 若
称为在
(2) 若
称为在
3.4 边缘概率密度和条件概率密度
3.4.1 边沿概率密度
二维连续型随机变量
3.4.2 条件概率密度
3.5 相互独立的随机变量
设
则称
3.5.1 离散型随机变量相互独立的判别定理
设二维离散型随机变量
则
3.5.2 连续型随机变量相互独立的判别定理
设二维连续型随机变量
则
第4章 复合随机变量和计算 笔记02的3
画图!
三角形区域(aX+bY+c)、圆形区域(
求的都是F,看题目,要是求概率密度函数f就再求导(含参变量积分的求导)
指数分布的最小值分布还是最小值
4.0 例题们
一维离散型随机变量
!一维连续 正态分布 概率密度
!!一维连续 均匀分布 概率密度
!!!一维连续
二维离散
!!!二维连续
!!!二维连续 MAX MIN
4.1 离散型随机变量的函数分布
4.1.1 一维离散型随机变量的函数分布律
定理
设离散型随机变量
- 若对于
- 若对于
4.1.2 二维离散型随机变量的函数分布律
定理
设离散型随机变量
- 若对于
- 对于
4.2 一维连续型随机变量的函数分布
定理
设连续型随机变量
其中
若函数
其中,
4.3 二维连续型随机变量的函数分布
一般方法:
几个具体函数的分布:
4.3.1
设二维连续型随机变量
- 设
4.3.2
设
4.3.3
设
4.3.4 旋转不变的随机变量
- 极坐标变换
- 设
第56章 数字特征和极限定理 笔记03的5 6
重要!!!!!!!!
绝对值分布,分部积分
5.0 例题们
正态分布的高阶矩计算
正态随机变量的绝对值分布和特征
随机向量的函数的数学期望
!!!离散型随机变量
正态分布的复合的期望方差
离散随机向量的数学期望
5.1 数学期望
5.1.1 离散型随机变量
定义
设
则称级数
5.1.2 离散型随机变量
定理
设
5.1.3 连续型随机变量
定义
设
5.1.4 连续型随机变量 X 的函数的数学期望
定理
设
5.1.5 随机向量的函数的数学期望
设
-
若
则有
其中
-
若
其中上式绝对收敛。
边缘分布的期望:特别的,令
5.1.6 数学期望的性质
-
设
-
设
-
设
-
设
5.2 方差
5.2.1 定义
若
称
5.2.2 方差的计算公式
方差
-
若
则:
-
若
-
简便计算公式
5.2.3 方差的性质
- 设
- 设
- !
- 设
5.3 常用随机变量的数学期望和方差
5.3.1 (0-1)分布,
5.3.2 二项分布,
5.3.3 泊松分布,
5.3.4 几何分布
5.3.5 超几何分布
按概率模型,超几何分布是n次无放回抽取到次品个数的概率分布,由抽签原理每次抽到次品服从两点分布
已知
故有
由和的方差公式有
5.3.6 均匀分布,
5.3.7 指数分布,
5.3.8 正态分布
定理1:正态分布的性质
- 设
定理2:
设随机变量
则
5.4 协方差和相关系数
5.4.1 协方差
定义
称数值
- 协方差为正,正相关
- 协方差为负,负相关
- 协方差为0,零相关
- 协方差绝对值越大,两个变量同或反向程度也越大
常用计算公式
协方差的性质
-
-
-
-
-
若
-
5.4.2 相关系数
定义
称数值
若
引入标准化随机变量
定理
若
即:
- 特殊情况:对二维正态分布,
性质
相关系数
柯西不等式
设
- 等式成立
定理
设
5.5 矩、协方差矩阵
5.5.1 矩
矩是一些数字特征的泛称或总称。
定义
设
- 若
- 若
数学期望
方差
此外,定义:
5.5.2 协方差矩阵
定义
对于
若
则矩阵
协方差矩阵
二维正态随机变量
若令
则有
于是
其中
6.0 例题们
马尔科夫不等式
数分?
依概率收敛
6.1 马尔科夫不等式和切比雪夫不等式
6.1.1 柯西施瓦茨不等式
- 柯西施瓦茨不等式
- 协方差不等式:
- 三角不等式:
6.1.2 马尔科夫不等式
设随机变量
6.1.3 切比雪夫不等式
设随机变量
固定
常数随机变量
- 常数随机变量:取值固定的随机变量,
- 推论
6.2 大数定律(依概率收敛)
6.2.1 定义
-
依次列出可数无穷多个随机变量
-
对于随机(变量)序列
或 或 则称随机(变量)序列
或 -
设随机变量序列
-
设有随机变量序列
-
设随机变量序列
6.2.2 切比雪夫弱大数定律
设
令
- 对任意
6.2.3 辛钦弱大数定律
若随机变量序列相互独立,存在相同的数学期望和方差
则对任意
其中
6.2.4 伯努利弱大数定律
设
表明
事件
6.2.5 *随机变量的三种收敛性
-
依概率收敛(Convergence in Probability)
依概率收敛是指一个随机变量序列
这意味着随着
弱大数定律都依概率收敛 -
以概率1收敛(Convergence Almost Surely):
以概率1收敛,也称为几乎处处收敛,是指一个随机变量序列
这意味着除了一个概率为0的事件之外,对于所有的样本点,随机变量序列
强大数定律以概率1收敛 -
依分布收敛(Convergence in Distribution):
依分布收敛,也称为弱收敛,是指一个随机变量序列
这里
中心极限定理是依分布收敛
这三种收敛方式之间的关系是:以概率1收敛蕴含依概率收敛,而依概率收敛蕴含依分布收敛。然而,反之则不一定成立。例如,依分布收敛的随机变量序列可能不依概率收敛,也不一定以概率1收敛。
6.3 中心极限定理(依分布收敛)
6.3.1 独立同分布的中心极限定理
设随机变量
定义部分和随机变量
当
应用
设随机变量
定义部分和随机变量
可以用逼近公式
特别二项分布
典型情形:设
6.3.2 De Moivre-Laplace 定理
设
数理统计
第7章 总体和分布 笔记03的7
7.0 例题们
正态分布、
正态分布、
正态分布、
正态分布、
7.1 总体与样本
7.1.1 总体与个体
- 总体:具有一定共同属性的研究对象的全体;
- 个体:组成总体的每一个元素
在实际中我们主要关心的是:研究对象的某一(或某几项)数量的指标
- 总体:随机变量(数量指标)
- 总体的分布:随机变量
7.1.2 样本值与样本
-
从一个总体
由于抽样的随机性,每次抽样结果是变化的。引入随机变量
称 -
总体就是一个随机变量
-
样本就是
-
按机会均等的原则,从总体中选取一些个体进行实验或观察的过程,称为随机抽样。
-
获得简单随机样本的方法是简单随机抽样。
7.1.3 样本分布
若总体
7.2 样本矩和统计量
7.2.1 样本矩(样本的矩统计量)
设
-
样本均值:
-
样本方差:
-
-
样本矩都是随机变量。
如果
分别是
7.2.2 统计量
设
显然,
如果
7.2.3 顺序统计量与经验分布函数
设
规定
记函数:
7.3 常用统计量的分布
7.3.1 正态总体样本的线性函数服从正态分布
设总体
特别地,当
常用结论:
7.3.2
定义
设
称
对于给定的正数
的点
对于不同的
性质
定理2:
若
定理3:
若
定理4:
设
其中
7.3.3
定义
设
称
对于给定的正数
数
则
称
对于不同的
定理6:
设
定理7:
设
7.3.4
设
称
对于给定的正数
第8章1-3 参数估计 笔记04的8:1-3
8.0 例题们
矩估计
极大似然估计
极大似然估计
证明无偏估计
最小方差无偏估计
一致性
8.1 参数的点估计
8.1.1 矩估计法
用样本矩估计相应的总体(随机变量)矩。
只要总体的
具体过程
设总体
- 求出总体矩:
- 对总体进行随机抽样,设
- 构造样本矩:
- 由于:
- 联立并解方程组求出
8.1.2 极大似然估计法
根据样本的具体情况,选择总体参数的估计,使得该样本发生的概率最大。
1 连续情形
定义
若
选取总体参数
单参数解法
- 求
- 解方程
- 经验证
多参数解法
- 求
- 解方程
- 经验证
2 离散情形
定义
若
选取总体参数
解法
同上
8.2 点估计的优良性
8.2.1 无偏性
设
证明
8.2.2 最小方差无偏估计(有效性)
设
则称
若
找
8.2.3 一致估计(相合性)
设
8.2.4 知识点
样本均值是期望的最小方差无偏线性估计MVU(样本均值作为总体期望的估计,具有无偏性和有效性)
样本方差是方差的无偏估计
正态总体的样本均值和样本方差的无偏和有效性
8.3 区间估计与置信区间
8.3.1 置信区间
设总体分布含有一未知参数
则称区间
注
- 统计量
对于
-
-
置信区间的长度意味着误差,因此越小越好
8.3.2 单侧置信限
若对于给定的
若对于给定的
第8章4第9章1-2 统计推断 笔记04的8:4 9:1-2
8.4 正态分布均值和方差的区间估计
8.4.1 均值
1.方差
设总体
求出统计量
区间
- 特别的,对于不服从正态分布的总体,只要n足够大,则由中心极限定理,随机变量
例
2.方差
设
故均值
其中
例1
例2
例3
8.4.2 方差
设总体
方差
注
选取的临界值
例
9.2 正态总体均值和方差的假设检验
假设检验过程中的两类判断错误(判断失误)
- 当判断
- 当判断
当样本容量
通常的实际做法是:设置检验水平
在实际问题中,如何给定检验水平
- 当拒绝一个属真的假设,即犯第一类错误后果非常严重时,应将
- 当取伪会引起严重后果时,可将
9.2.1
1.
由样本提供的信息计算
- 若
- 若
例
2.
由样本提供的信息计算出
- 若
- 若
例
3.
由样本提供的信息计算出
- 若
- 若
例
9.2.2
1.
由样本计算出
- 若
- 若
例1
例2
2.
由样本计算出
- 若
- 若
3.
由样本计算出
- 若
- 若
以上三种检验法均采用了
9.2.3 正态总体方差的假设检验
1. 检验假设
根据样本值计算
- 若
- 否则接受假设
例1
例2
2. 检验假设
根据样本值计算
- 若
- 否则接受假设
3. 检验假设
根据样本值计算
- 若
- 否则接受假设
例
注:假设检验与置信区间的关系
假设
随机过程
第10章 随机过程的基本概念 笔记04的10
10.1 随机过程的定义及分类
10.1.1 随机过程的定义
定义1
给定参数集
对任意给定的
定义2
设随机试验
对于所有的
由定义2得
- 对于
- 对任意给定的
定义3
定义在
对于固定的
例
10.1.2 随机过程的分类
1. 按随机过程的参数集和状态空间分类
- 参数集
- 状态空间
参数离散随机过程是随机变量序列,简称随机序列。
一般地记
2. 按随机过程的概率结构分类
- 二阶矩过程,包括正态过程,平稳过程等
- 马尔可夫过程
- 马尔科夫链
- 泊松过程
- 维纳过程
- 扩散过程
- 更新过程
- 鞅
10.2 随机过程的概率分布
10.2.1 随机过程的n维分布函数
设
称为随机过程
如果存在非负函数
成立,则称
10.2.2 独立过程
如果对于任何正整数
独立过程的
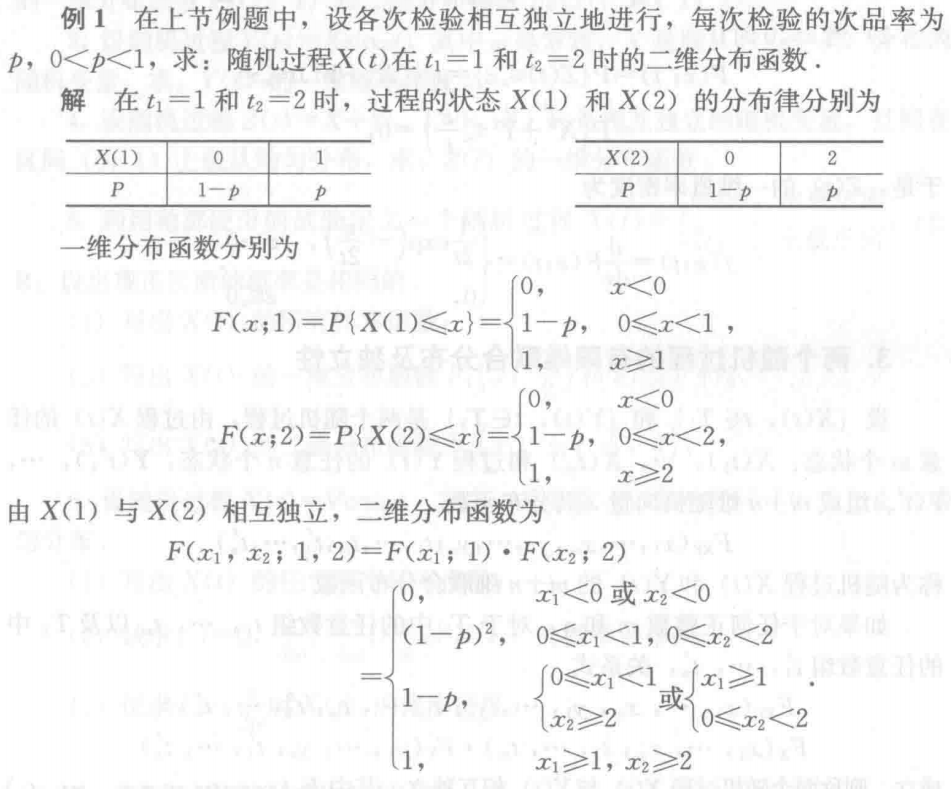
例
10.2.3 两个随机过程的有限维联合分布及独立性
设
称为随机过程
如果对于任何正整数
都成立,则称两个随机过程相互独立。
10.3 随机过程的数字特征
10.3.1 随机过程的数字特征
参数集
-
过程在
对于一切
-
过程在
称为随机过程
-
过程在
称为随机过程
-
任选
称为随机过程
-
称为随机过程
- 均值、均方值、方差是刻画随即过程在各个状态的统计特性
- 相关函数和协方差函数是刻画随机过程的任何两个不同状态的统计特性
数字特征间的关系
10.3.2 连续型随机过程的数字特征
对连续型随机过程
任选
例1
例2
10.3.3 两个随机过程的互相关函数
两个随机过程
-
称为随机过程
-
称为随机过程
且有 -
如果对任意
显然,两个相互独立的随机过程必不相关
例
第11章 平稳过程 笔记04的11
11.1 严平稳过程
11.1.1 严平稳过程的定义
对于任意实数
(严平稳条件)
则
若参数
11.1.2 严平稳过程的性质
- 状态离散的随机过程
- 状态连续的随机过程
- 特殊地,取
- 一维分布函数
- 二维分布函数
- 一维分布函数
- 一维分布函数
- 二维分布函数
11.1.3 严平稳过程的数字特征
定理
设
注:
这一性质也称为数字特征的平稳性
例 伯努利过程
11.2 宽(广义)平稳过程
11.2.1 宽平稳过程的定义
设随机过程
则称
参数集
11.2.2 平稳过程的例子
例1 证明是平稳过程
例2 证明是平稳过程
例3 证明是平稳序列
例4 证明是平稳序列
例5 证明是平稳过程
11.2.3 严平稳过程与宽平稳过程的关系
- 宽平稳过程不一定是严平稳过程
- 严平稳过程不一定是宽平稳过程
- 存在二阶矩的严平稳过程必定是宽平稳过程
二阶矩
11.2.4 两个平稳过程的关系:平稳相关
设
定义:
称为标准互协方差函数。
11.3 正态平稳过程
11.3.1 正态过程的概念
1. 正态随机变量的有关知识
一维正态随机变量
二维正态随机变量
其中:
协方差矩阵
2. 正态过程的定义
如果随机过程
设
3. 独立正态过程的定义
如果
正态过程
4. 正态过程是二阶矩过程
设
必存在,即二阶矩存在。
11.3.2 正态平稳过程
1. 定义
如果正态过程
2. 定理
设
3. 例题
例1 正态平稳过程的一维、二维服从的分布
例2 证明平稳过程
11.4 遍历过程(经历过程)
11.4.1 时间均值和时间相关函数
设随机过程
固定
\overline{x(t)} = \overline{X(e,t)} = \lim\limits{l \to +\infty}
\dfrac{1}{2l}\int^l{-l}X(e, t),dt
\begin{aligned}
\overline{X(t)X(t + \tau)}
= & \overline{X(e, t)X(e, t + \tau)}\
= & \lim\limits{l \to +\infty}
\dfrac{1}{2l}
\int^l{-l}
X(e, t)X(e, t + \tau),dt
\end{aligned}
\begin{aligned}
&\overline{X(t)} = \lim\limits{l \to +\infty}
\dfrac{1}{l}
\int_0^l X(e, t), dt\
&\overline{X(t)X(t + \tau)} = \lim\limits{l \to +\infty}
\dfrac{1}{l}
\int_0^l X(e, t)X(e, t + \tau), dt
\end{aligned}
\lim\limits_{l \to +\infty}
\dfrac{1}{l} \int_0^{2l}
(1 - \dfrac{\tau}{2l})[R_X(\tau) - \mu^2_X],d\tau = 0
\lim\limits_{l \to +\infty}
\dfrac{1}{l} \int_0^{l}
(1 - \dfrac{\tau}{l})[R_X(\tau) - \mu^2_X],d\tau = 0
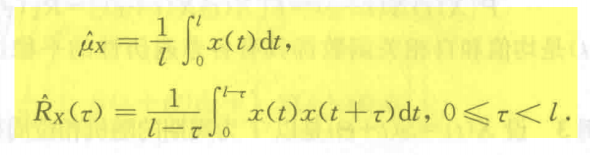 ## 第12章 <span style="background:#ff4d4f">马尔科夫链引论</span> 笔记04的12
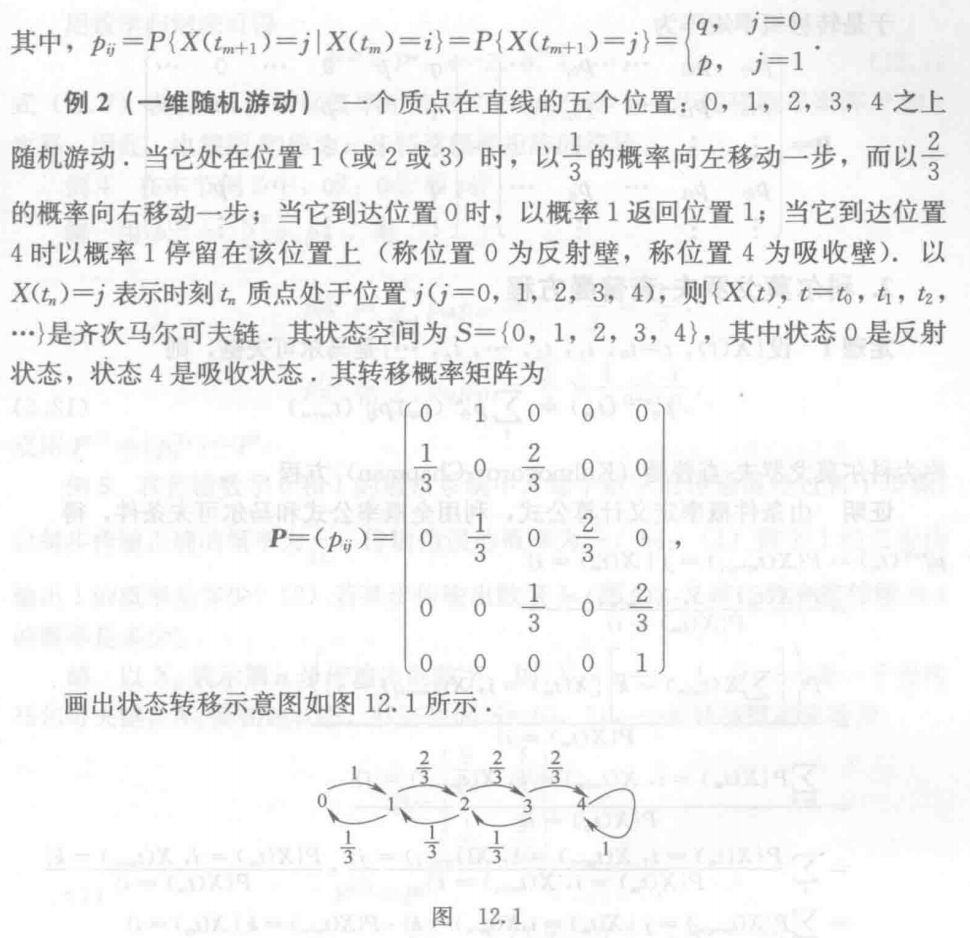
## 第12章 <span style="background:#ff4d4f">马尔科夫链引论</span> 笔记04的12  马尔科夫链必考 ## 12.2 参数离散的齐次马尔可夫链 ### 12.2.1 转移概率矩阵 ##### 定义 设 $\{X(t), t = t_0, t_1, t_2, ..., t_n, ...\}$ 是齐次马尔可夫链,由于状态空间 $S$ 是离散的,不妨设 $S=\{0, 1, 2, ...,n, ...\}$ 则对 $S$ 内的任意两个状态 $i$ 和 $j$,由转移概率 $p_{ij}=P\{X(t_{m+1})=j|X(t_m)=i\}$ 排序一个矩阵:
马尔科夫链必考 ## 12.2 参数离散的齐次马尔可夫链 ### 12.2.1 转移概率矩阵 ##### 定义 设 $\{X(t), t = t_0, t_1, t_2, ..., t_n, ...\}$ 是齐次马尔可夫链,由于状态空间 $S$ 是离散的,不妨设 $S=\{0, 1, 2, ...,n, ...\}$ 则对 $S$ 内的任意两个状态 $i$ 和 $j$,由转移概率 $p_{ij}=P\{X(t_{m+1})=j|X(t_m)=i\}$ 排序一个矩阵:P=
\left(
\begin{array}
&p{00}&p{01}&\cdots&p{0j}&\cdots\
p{10}&p{11}&\cdots&p{1j}&\cdots\
\vdots&\vdots&\ddots&\vdots&\cdots\
p{i0}&p{i1}&\cdots&p_{ij}&\cdots\
\vdots&\vdots&\vdots&\vdots&\ddots
\end{array}
\right)
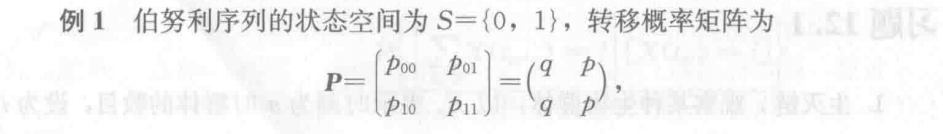

 ### 12.2.2 科尔莫戈罗夫-查普曼方程 ##### 定理 设 $\{X(t), t=t_0, t_1, t_2, ..., t_n, ...\}$ 是参数离散的马尔可夫链,$S$ 为其状态空间,则有:
### 12.2.2 科尔莫戈罗夫-查普曼方程 ##### 定理 设 $\{X(t), t=t_0, t_1, t_2, ..., t_n, ...\}$ 是参数离散的马尔可夫链,$S$ 为其状态空间,则有:p{ij}^{(n+l)}(t_m)=
\sum\limits{k \in S} p{ik}^{(n)}(t_m) \cdot p^{(l)}{kj}(t_{m+n})


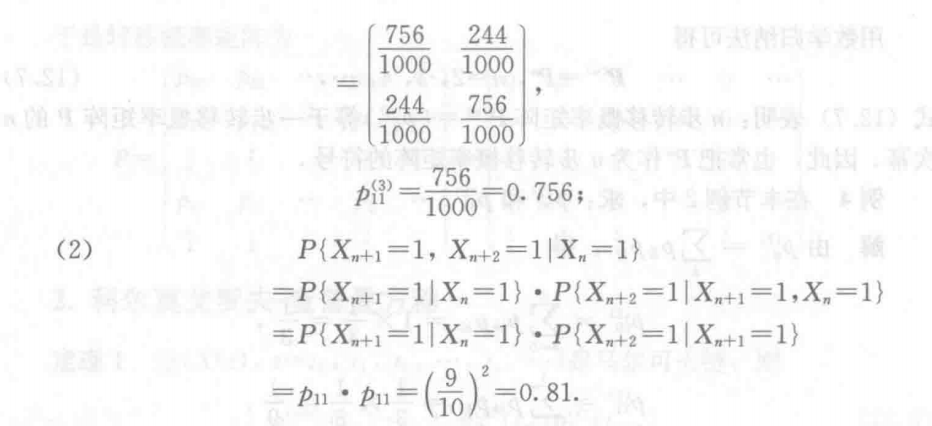 ### 12.2.3 有限维概率分布 #### 1. 初始分布(初始概率) 马氏链 $\{X(t), t = t_0, t_1, t_2, ...\}$ 在初始时刻 $t_0$ 的一维概率分布:
### 12.2.3 有限维概率分布 #### 1. 初始分布(初始概率) 马氏链 $\{X(t), t = t_0, t_1, t_2, ...\}$ 在初始时刻 $t_0$ 的一维概率分布:p_{j}(t_0)=P{X(t_0)=j}, \quad j=0, 1, 2, ...
\begin{aligned}
&P{X(k1) = j_1, X(k_2)=j_2, ..., X(k_n) = j_n}\
=& \sum\limits{i=0}^{+\infty}pi(0)\cdot p{ij1}^{(k_1)}\cdot p{j1j_2}^{(k_2 - k_1)}...p{j{n-1}j_n}^{(k_n-k{n-1})}
\end{aligned}
 #### 3. 绝对分布(绝对概率,瞬时概率) 马尔可夫链在任何时刻 $t_n$ 的一维概率分布:
#### 3. 绝对分布(绝对概率,瞬时概率) 马尔可夫链在任何时刻 $t_n$ 的一维概率分布:p_j(t_n)=P{X(t_n)=j},\quad j = 0,1,2,...
pj(t_n)=\sum\limits{i=0}^{+\infty} pi(t_0)\cdot p{ij}^{(n)},\quad j=0, 1, 2,...
\begin{aligned}
&\big(p_0(t_n), p_1(t_n), ..., p_j(t_n), ...\big)\
=&\big(p_0(t_0), p_1(t_0), ..., p_j(t_0), ...\big)\cdot P^n
\end{aligned}


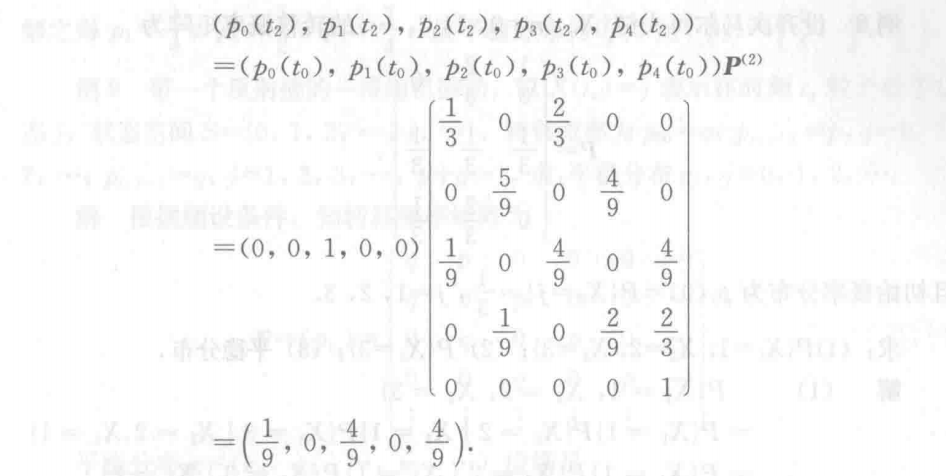 ### 12.2.4 平稳分布 ##### 定义 对于齐次马尔可夫链 $\{X(t), t = t_0, t_1, t_2, ...\}$,如果存在一维概率分布 $p_j\space j=1,2,...$,满足:
### 12.2.4 平稳分布 ##### 定义 对于齐次马尔可夫链 $\{X(t), t = t_0, t_1, t_2, ...\}$,如果存在一维概率分布 $p_j\space j=1,2,...$,满足:pj=\sum\limits{i=0}^{+\infty}pip{ij}
(p_0, p_1, p_2, ..., p_j, ...)=(p_0, p_1, p_2, ..., p_j, ...)\cdot P
p_j(t_n) = P{X(t_n)=j}=p_j(t_0),\space j=0,1,2,...
\big(p_0(t_n), p_1(t_n), ..., p_j(t_n), ...\big)
=\big(p_0(t_0), p_1(t_0), ..., p_j(t_0), ...\big)