1 Python代码
import numpy as np
from scipy.integrate import quad
import matplotlib.pyplot as plt
from scipy.special import chebyt # 切比雪夫多项式
# --------------------------
# 1. 核心参数与被逼近函数定义
# --------------------------
# 被逼近函数 f(x) = sqrt(1 - x²),定义域[-1,1]
def f(x):
return np.sqrt(1 - x**2)
# 切比雪夫多项式的权函数 ρ(x) = 1/√(1 - x²)
def rho(x):
return 1 / np.sqrt(1 - x**2)
# 逼近次数(8次和10次)
n8 = 8 # 8次逼近:使用T0-T8
n10 = 10 # 10次逼近:使用T0-T10
# --------------------------
# 2. 计算切比雪夫最佳平方逼近系数
# --------------------------
def compute_chebyshev_coeffs(n):
"""
计算n次切比雪夫多项式逼近的系数a_k(文档1-130公式)
a_k = (f, T_k) / (T_k, T_k),其中内积(f, T_k) = ∫[-1,1] f(x)T_k(x)ρ(x)dx
"""
coeffs = np.zeros(n + 1) # coeffs[0]对应a0,coeffs[k]对应ak
for k in range(n + 1):
# 切比雪夫多项式T_k(x)
Tk = chebyt(k)
# 计算内积(f, T_k) = ∫[-1,1] f(x)*Tk(x)*rho(x)dx
# 注:f(x)*rho(x) = sqrt(1-x²)*1/sqrt(1-x²) = 1,简化积分
def inner_product_integrand(x):
return f(x) * Tk(x) * rho(x)
(f_Tk, _) = quad(inner_product_integrand, -1, 1) # 数值积分计算内积
# 计算内积(T_k, T_k)
if k == 0:
Tk_Tk = np.pi # k=0时,(T0,T0)=π
else:
Tk_Tk = np.pi / 2 # k≥1时,(Tk,Tk)=π/2
# 计算系数ak
coeffs[k] = f_Tk / Tk_Tk
return coeffs
# --------------------------
# 3. 构建切比雪夫逼近多项式
# --------------------------
def chebyshev_approximation(x, coeffs):
"""
由系数coeffs构建逼近多项式 C(x) = Σ[0..n] a_k*T_k(x)
"""
n = len(coeffs) - 1 # 逼近次数
C = 0.0
for k in range(n + 1):
Tk = chebyt(k)
C += coeffs[k] * Tk(x)
return C
# --------------------------
# 4. 计算逼近误差(均方误差与最大误差)
# --------------------------
def compute_approximation_error(f, C, x_range):
"""
计算逼近误差:
- 均方误差(文档1-86最佳平方逼近定义):sqrt(∫[-1,1] ρ(x)[f(x)-C(x)]²dx)
- 最大误差:max|f(x)-C(x)|(区间[-1,1]内)
"""
# 计算均方误差
def mse_integrand(x):
return rho(x) * (f(x) - C(x))**2
(mse_integral, _) = quad(mse_integrand, -1, 1)
rmse = np.sqrt(mse_integral) # 均方根误差(更直观)
# 计算最大误差(在密集采样点上评估)
x_samples = np.linspace(x_range[0], x_range[1], 1000) # 1000个采样点
f_samples = f(x_samples)
C_samples = C(x_samples)
max_error = np.max(np.abs(f_samples - C_samples))
return rmse, max_error
# --------------------------
# 5. 主流程:计算+可视化
# --------------------------
if __name__ == "__main__":
# 步骤1:计算8次和10次逼近的系数
coeffs8 = compute_chebyshev_coeffs(n8)
coeffs10 = compute_chebyshev_coeffs(n10)
# 步骤2:定义逼近多项式(输入x,输出逼近值)
def C8(x):
return chebyshev_approximation(x, coeffs8)
def C10(x):
return chebyshev_approximation(x, coeffs10)
# 步骤3:计算误差
x_range = (-1, 1)
rmse8, max_error8 = compute_approximation_error(f, C8, x_range)
rmse10, max_error10 = compute_approximation_error(f, C10, x_range)
# 步骤4:输出结果
print("="*60)
print("切比雪夫多项式最佳平方逼近结果")
print("="*60)
print(f"8次逼近(T0-T8):")
print(f" 系数a0~a8:{coeffs8.round(6)}")
print(f" 均方根误差(RMSE):{rmse8:.6f}")
print(f" 最大误差([-1,1]):{max_error8:.6f}")
print(f"\n10次逼近(T0-T10):")
print(f" 系数a0~a10:{coeffs10.round(6)}")
print(f" 均方根误差(RMSE):{rmse10:.6f}")
print(f" 最大误差([-1,1]):{max_error10:.6f}")
print("="*60)
# 步骤5:可视化对比(原函数 vs 8次逼近 vs 10次逼近)
x_plot = np.linspace(-1, 1, 1000)
f_plot = f(x_plot)
C8_plot = C8(x_plot)
C10_plot = C10(x_plot)
plt.figure(figsize=(12, 8))
# 子图1:函数逼近效果
plt.subplot(2, 1, 1)
plt.plot(x_plot, f_plot, label="原函数 $f(x)=\sqrt{1-x^2}$", linewidth=2, color="black")
plt.plot(x_plot, C8_plot, label="8次切比雪夫逼近", linewidth=1.5, color="red", linestyle="--")
plt.plot(x_plot, C10_plot, label="10次切比雪夫逼近", linewidth=1.5, color="green", linestyle="-.")
plt.xlabel("x")
plt.ylabel("y")
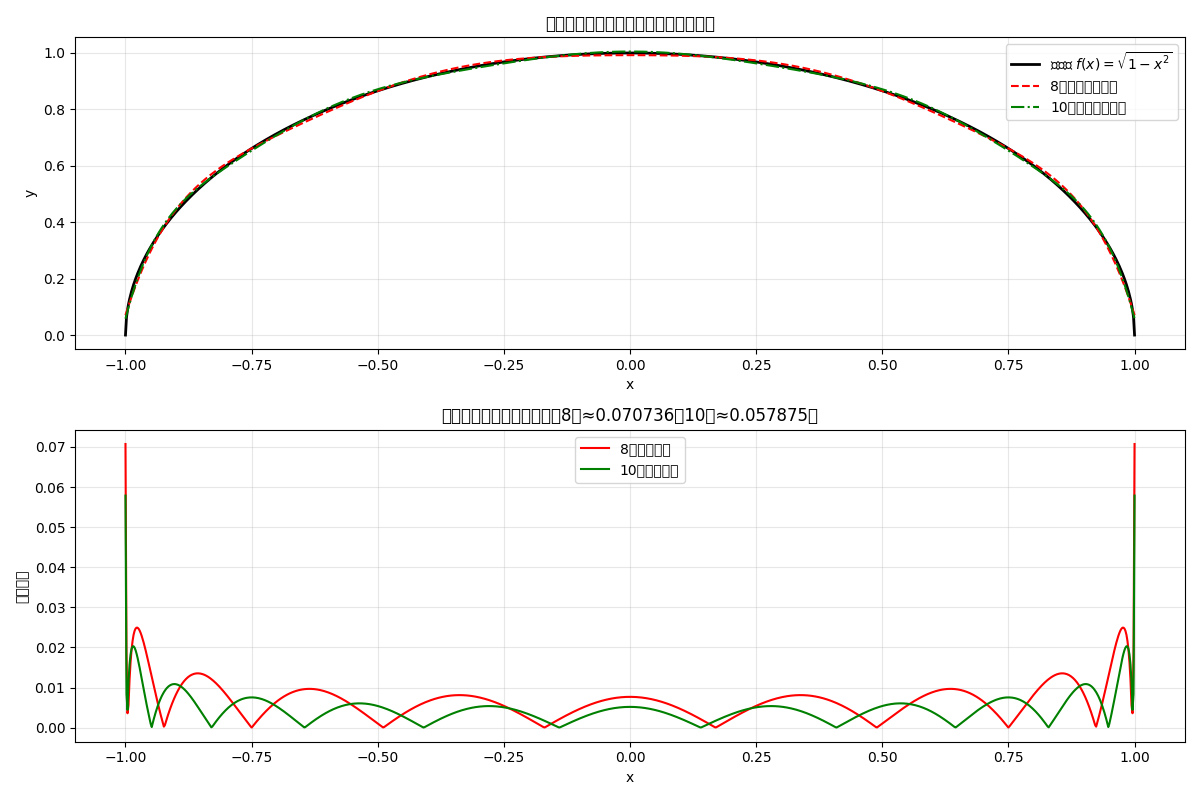
plt.title("切比雪夫多项式最佳平方逼近效果对比")
plt.legend()
plt.grid(True, alpha=0.3)
# 子图2:逼近误差
plt.subplot(2, 1, 2)
error8_plot = np.abs(f_plot - C8_plot)
error10_plot = np.abs(f_plot - C10_plot)
plt.plot(x_plot, error8_plot, label="8次逼近误差", linewidth=1.5, color="red")
plt.plot(x_plot, error10_plot, label="10次逼近误差", linewidth=1.5, color="green")
plt.xlabel("x")
plt.ylabel("绝对误差")
plt.title("逼近误差对比(最大误差:8次≈{:.6f},10次≈{:.6f})".format(max_error8, max_error10))
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
2 结果和分析
============================================================
切比雪夫多项式最佳平方逼近结果
============================================================
8次逼近(T0-T8):
系数a0~a8:[ 0.63662 0. -0.424413 0. -0.084883 0. -0.036378
0. -0.02021 ]
均方根误差(RMSE):0.024013
最大误差([-1,1]):0.070736
10次逼近(T0-T10):
系数a0~a10:[ 0.63662 0. -0.424413 0. -0.084883 0. -0.036378
0. -0.02021 0. -0.012861]
均方根误差(RMSE):0.017799
最大误差([-1,1]):0.057875
============================================================
两类逼近的误差数据及提升幅度整理如下表:
| 误差指标 | 8次逼近 | 10次逼近 | 精度提升幅度 |
|---|---|---|---|
| 均方根误差(RMSE) | 0.024013 | 0.017799 | ≈25.88% |
| 最大误差([-1,1]区间) | 0.070736 | 0.057875 | ≈18.18% |
10 次切比雪夫多项式通过新增高次修正项,在整体精度(RMSE 提升 25.88%)和最坏情况精度(最大误差提升 18.18%)上均优于 8 次逼近,且符合切比雪夫逼近的理论规律。实际应用中,需结合精度需求与计算成本,合理选择逼近次数,实现“精度-效率”的最优平衡。
- 高次修正项的补充作用
对比两类逼近的系数可知,10次逼近在8次逼近系数基础上,仅新增10次项系数,其余低次项系数完全一致。这一高次项的核心作用是“细节补偿”——低次项(T0、T2等)已构建出原函数的整体轮廓,而10次项(T10(x))针对低次逼近未覆盖的细微曲线偏差进行修正,尤其对原函数在x=±1附近的陡峭区域拟合更精准,从而降低了最大误差;同时,全局范围内的细微偏差累积减少,使得RMSE大幅下降。 - 误差指标的物理意义差异
RMSE反映区间内整体误差的平均水平,对全局偏差更敏感,因此10次项的全局修正使其提升幅度更大;最大误差则聚焦区间内“最难拟合点”(如x=±1附近,原函数导数趋于无穷大),这类点的偏差修正受函数本身陡峭特性限制,因此提升幅度相对平缓,但仍实现了近18%的改善,证明高次项对敏感区域的拟合有效性。