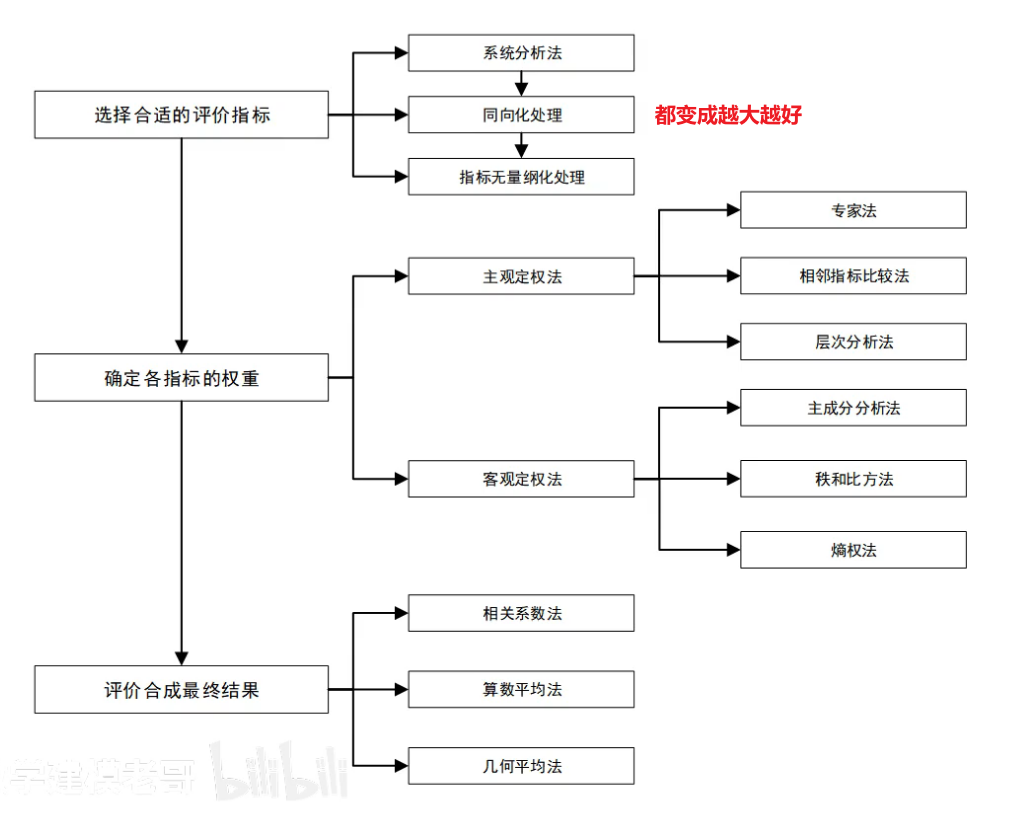
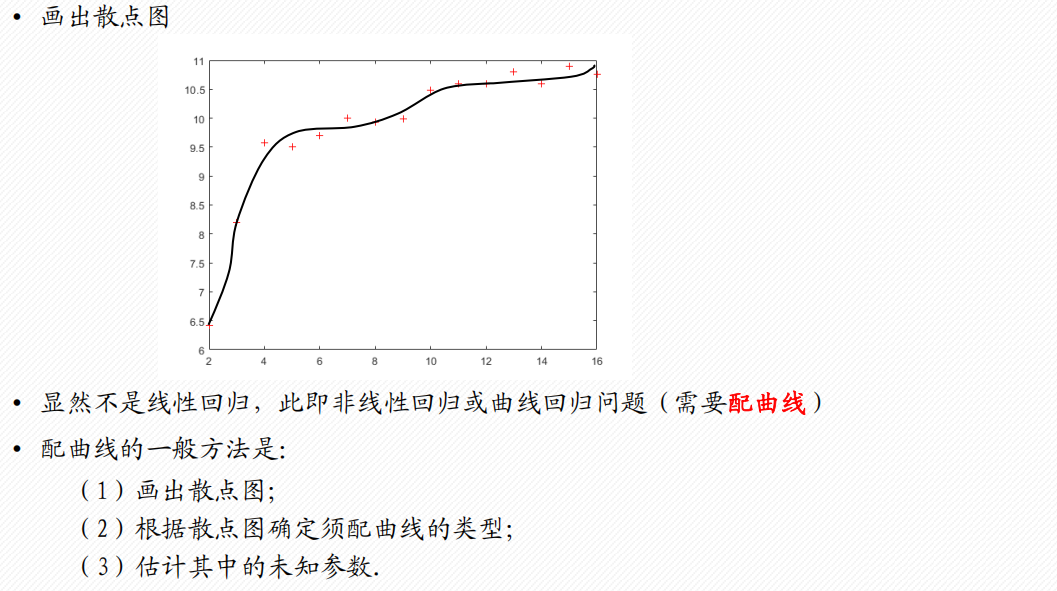
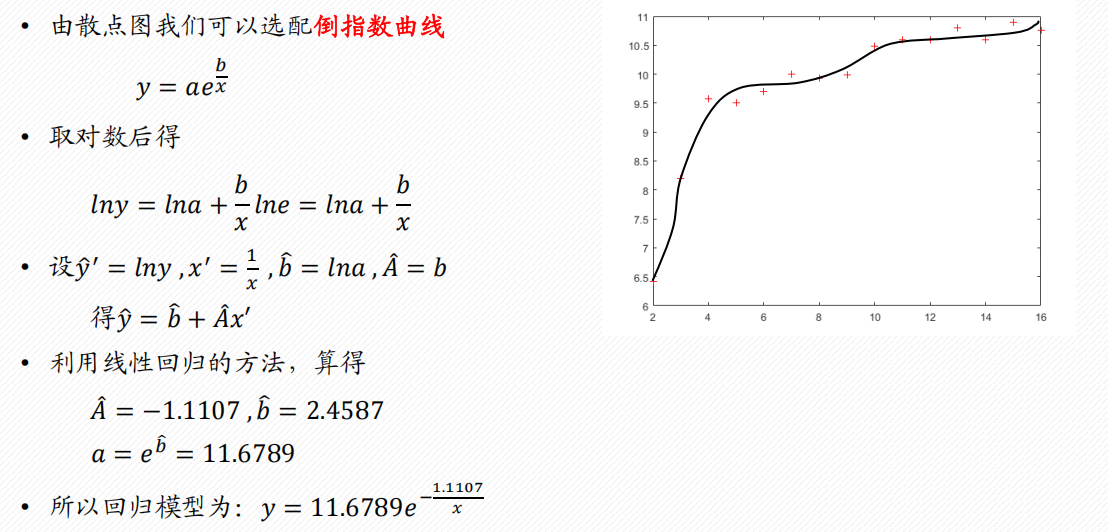
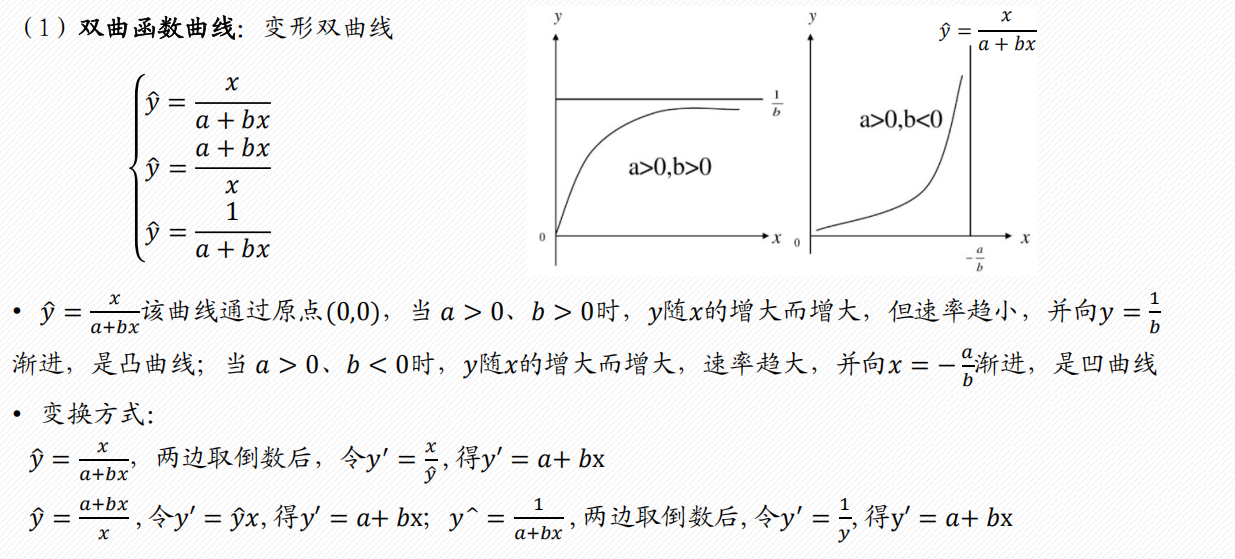
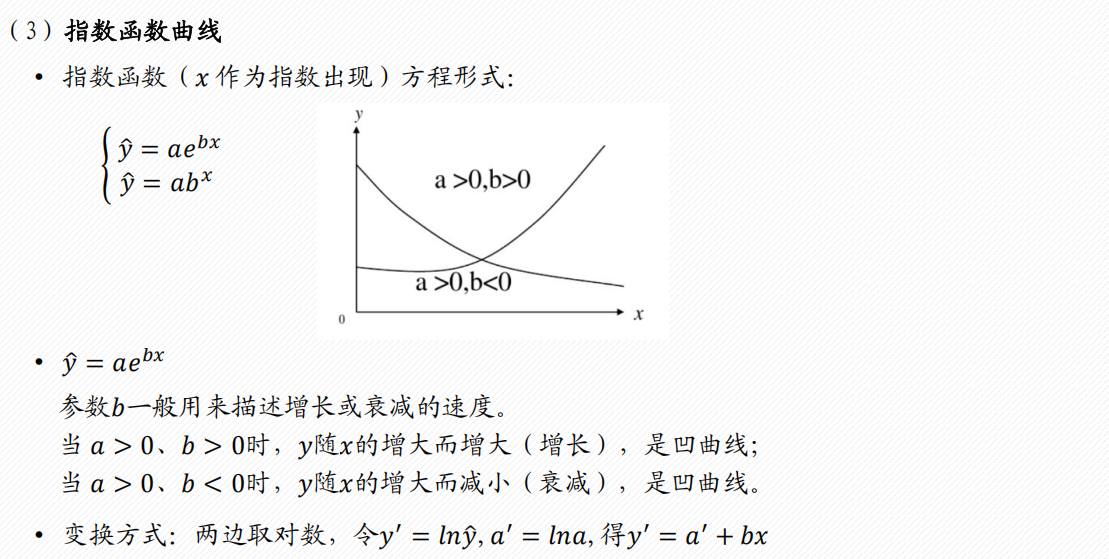
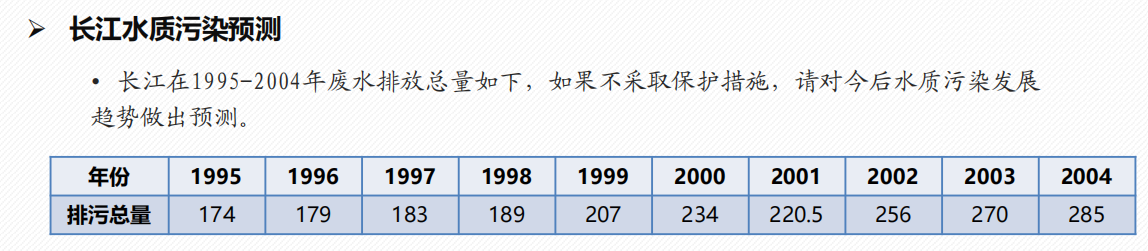
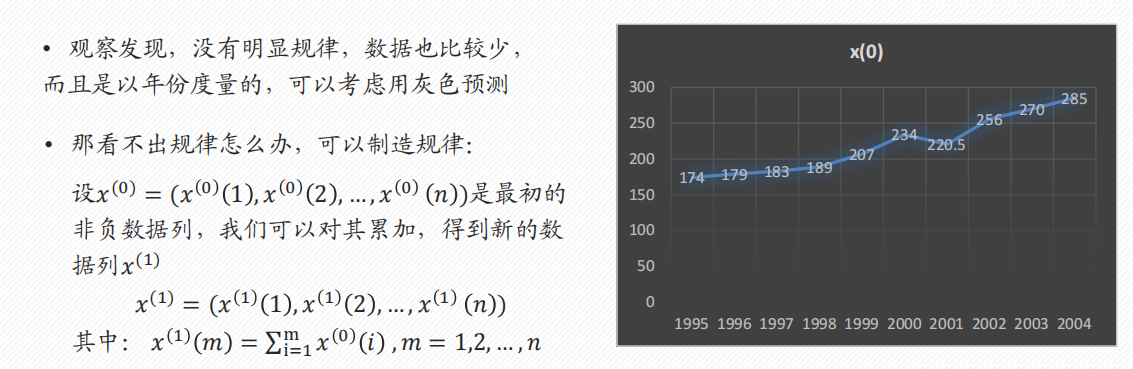
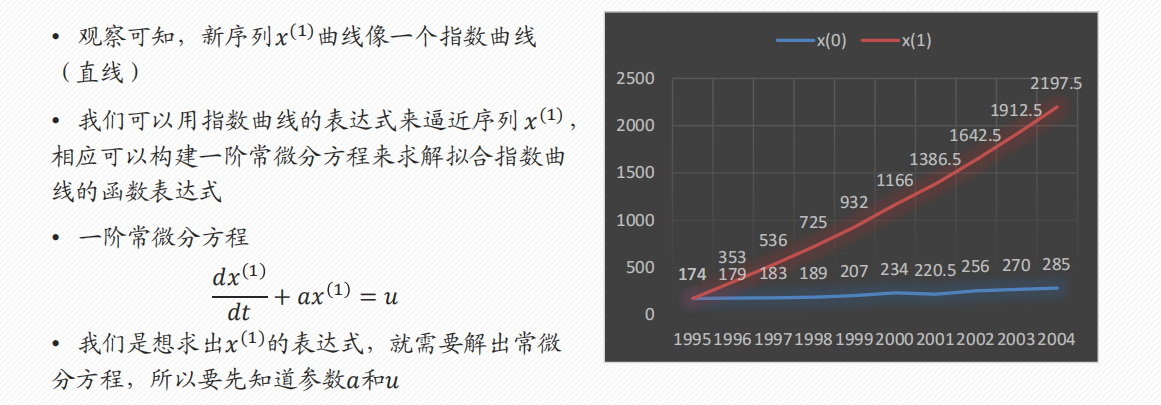
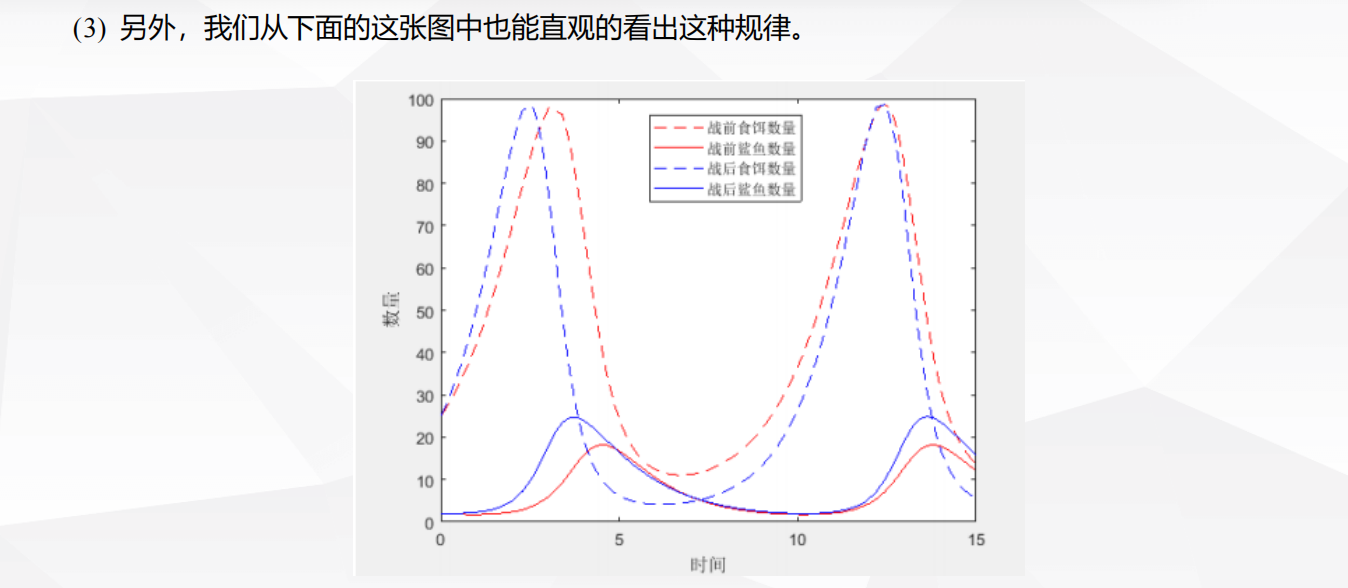
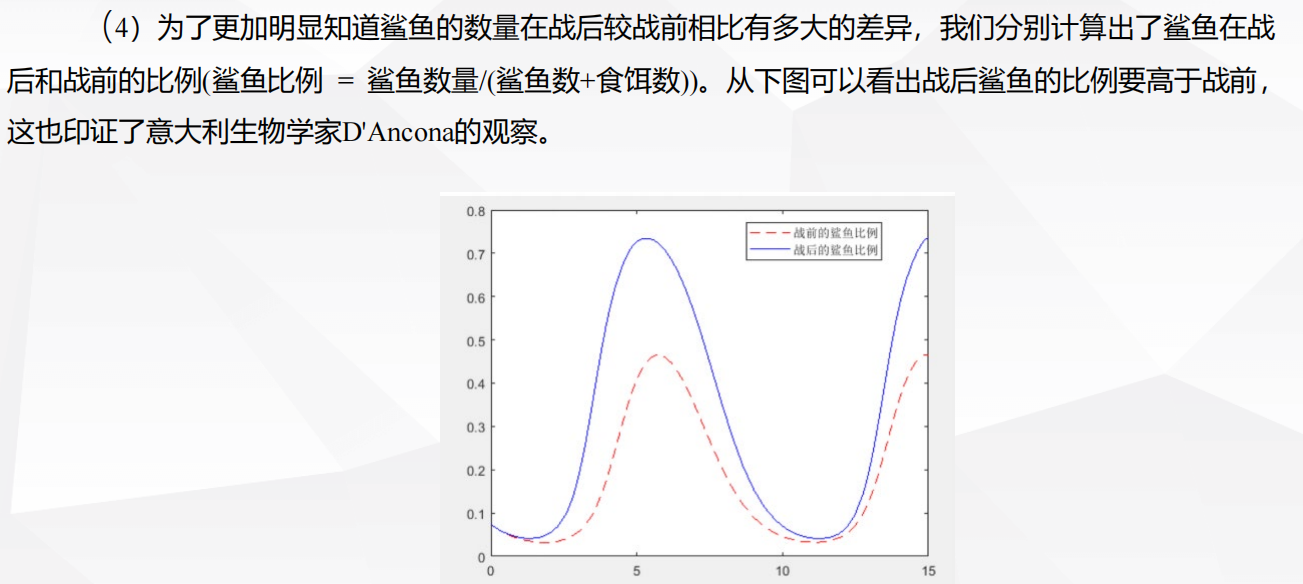
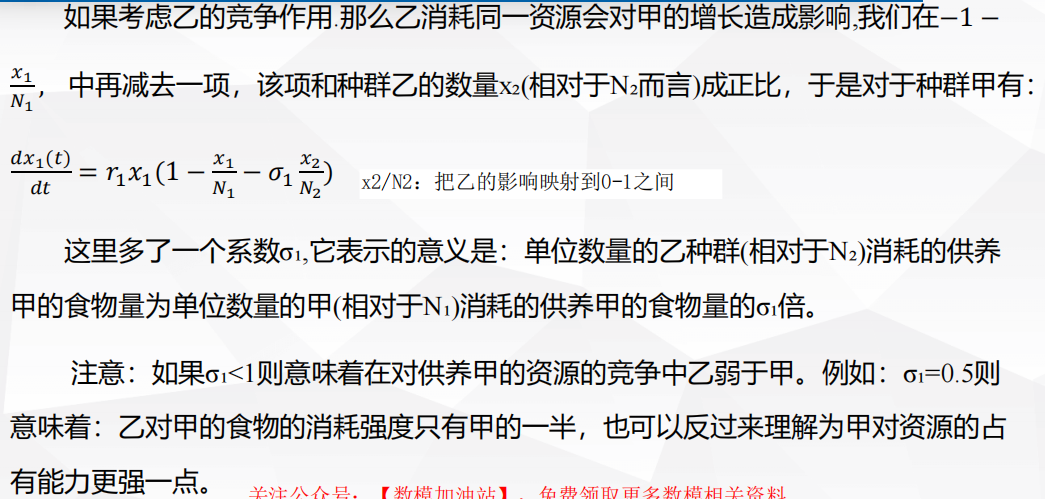
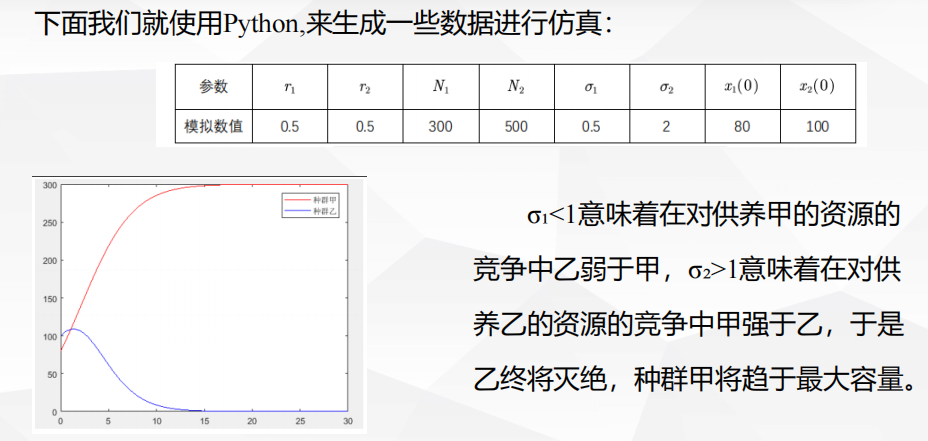
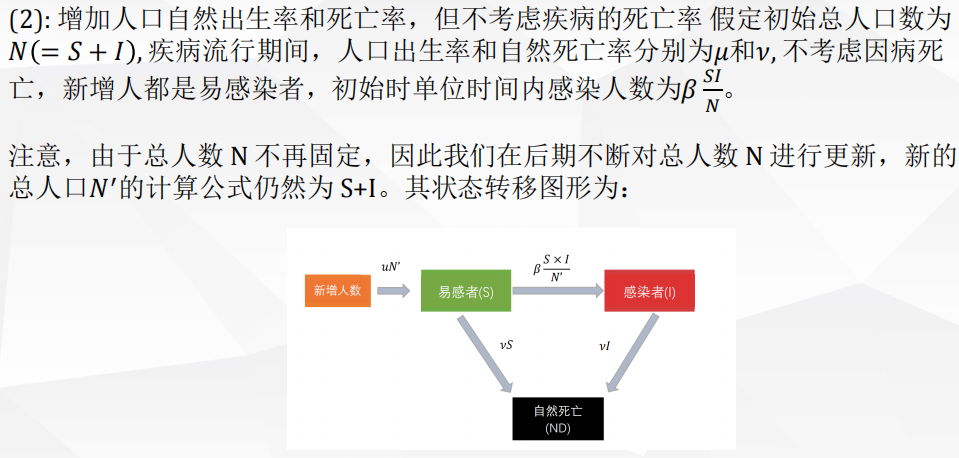
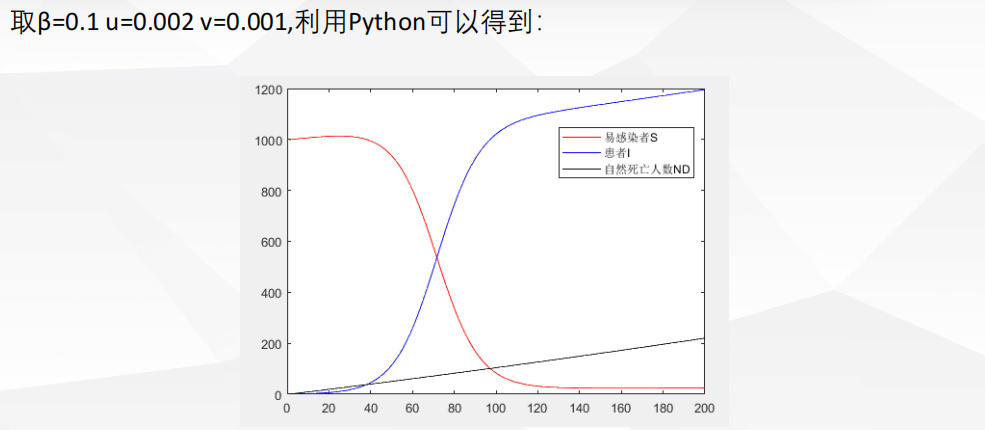
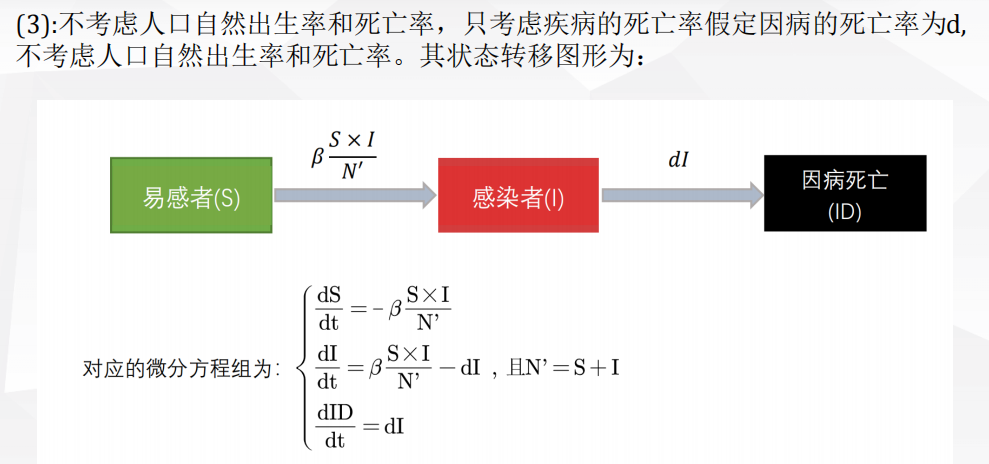
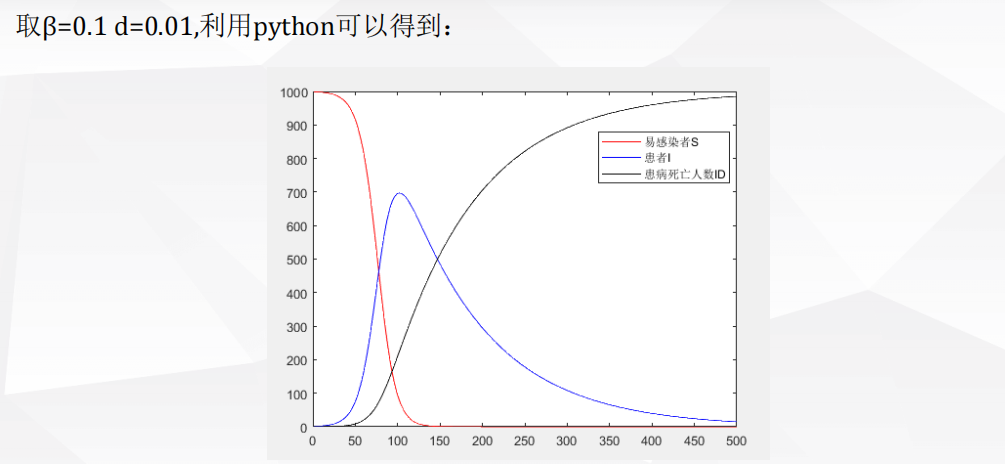
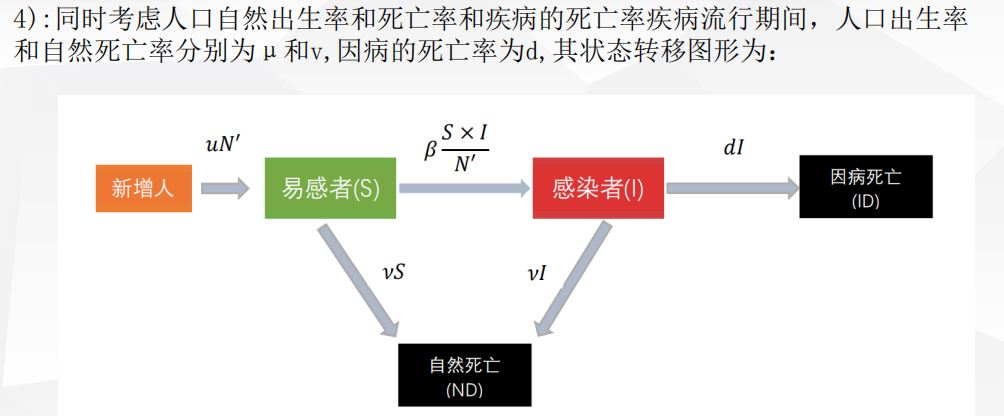
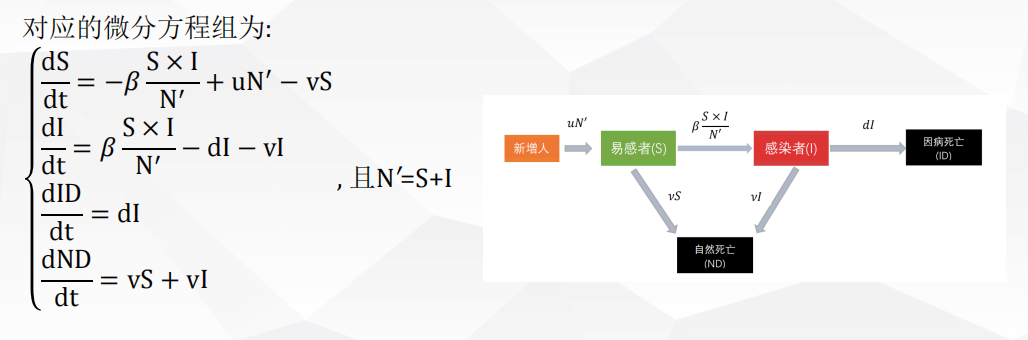
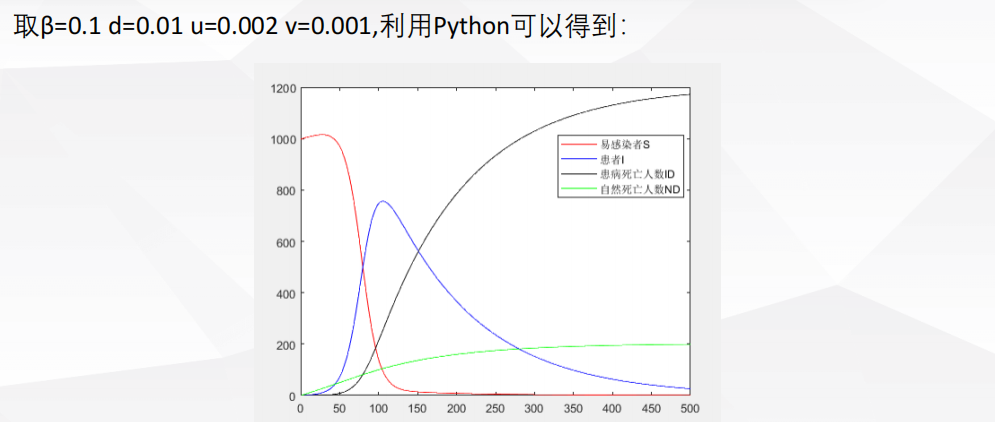
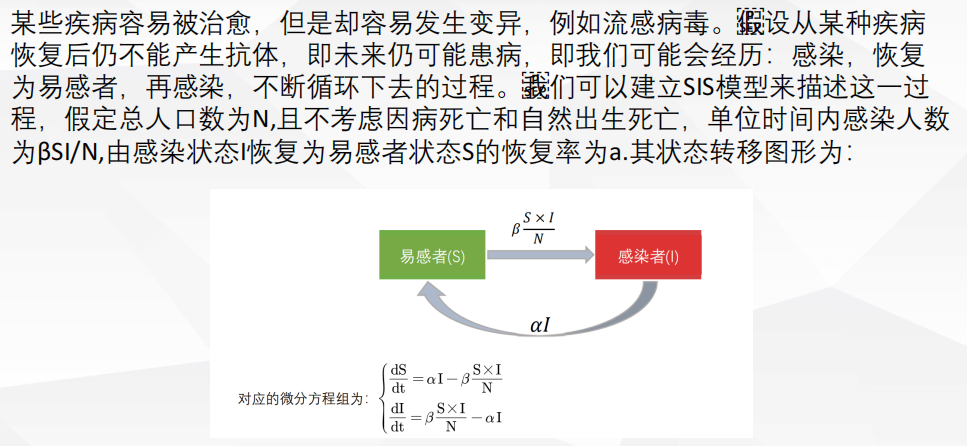
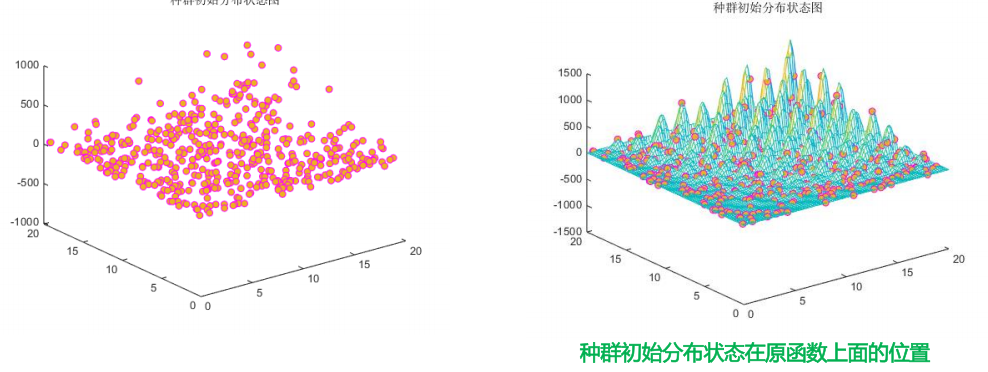
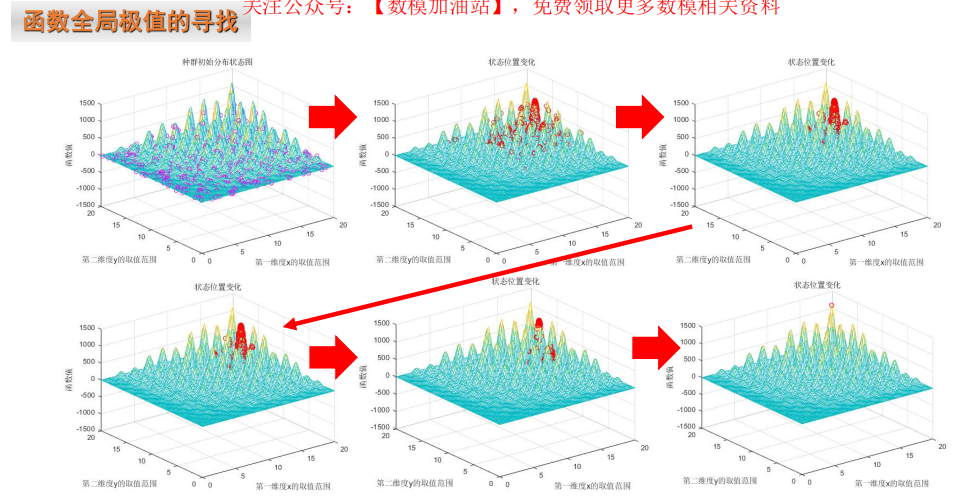
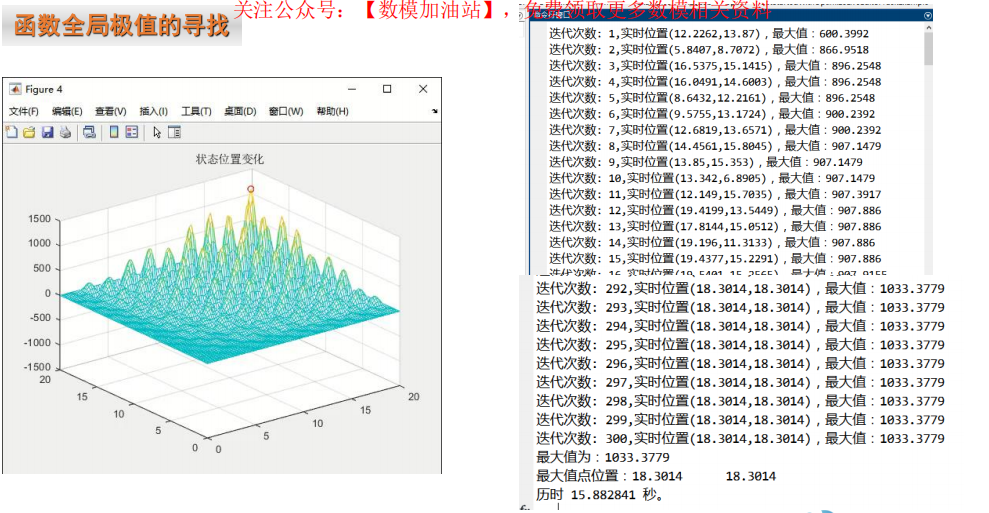
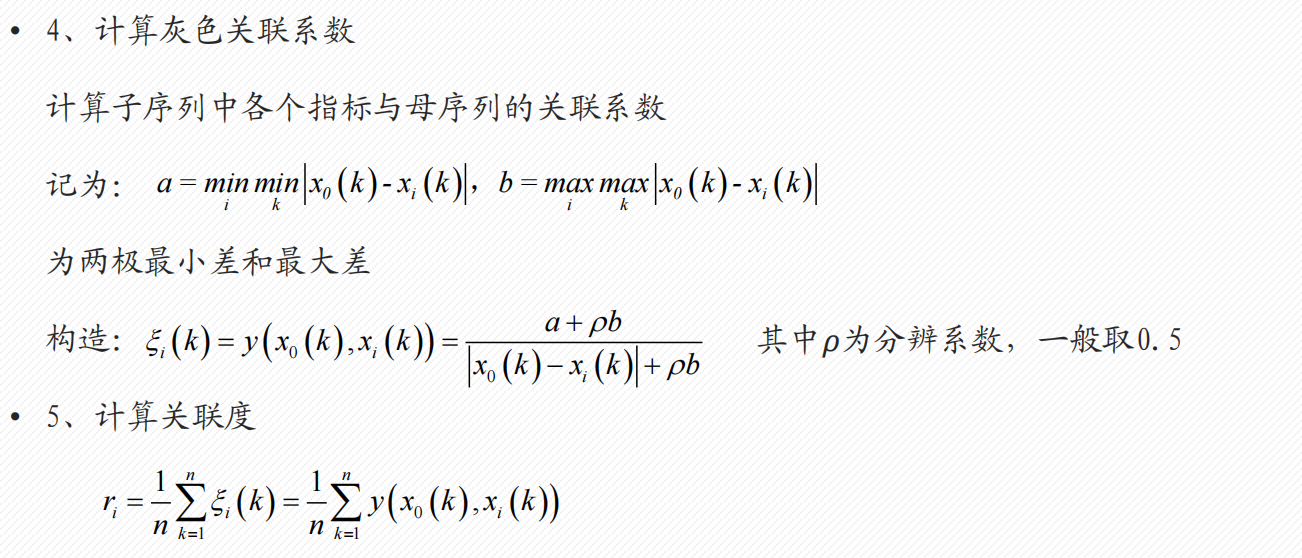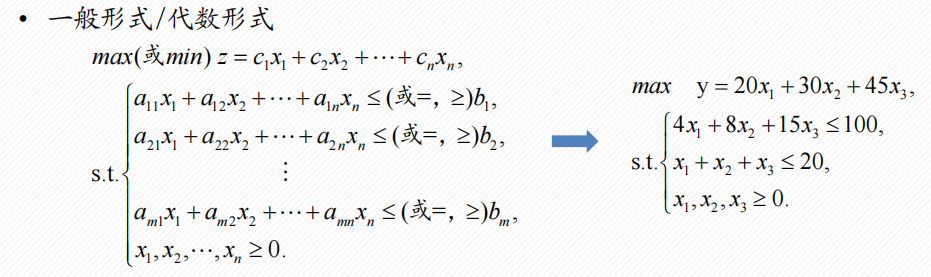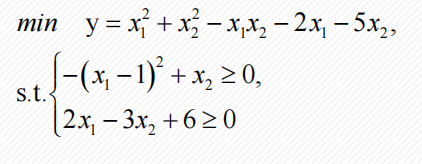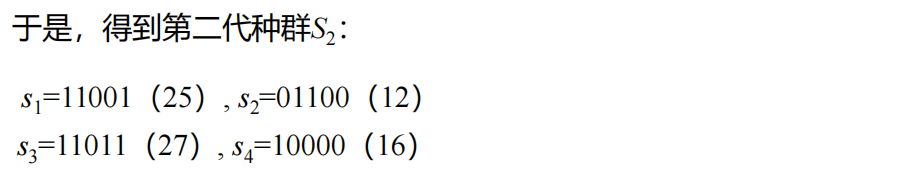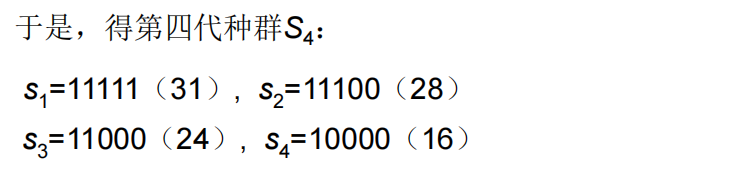1 评价决策类

评价或选择一个可能更好或更优的政策或方案，要先找到指标，再量化指标，再综合考虑所有指标


AHP确定各个成分的权重，TOPSIS进行评价
降维：TSNE降维方法 > 主成分分析

1.1 层次分析法 ( AHP )

• 适用于那些难于完全定量分析的问题
• 可用来求权重，较为主观：TOPSIS

基本原理

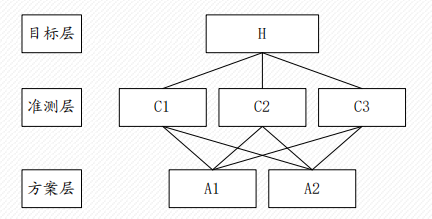
首先要把问题条理化、层次化，构造出一个有层次的结构模型。这些层次可以分为三类：

• 最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。（选出微博之星）
• 中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、指标、子准则，因此也称为准则层。（粉丝数、作品、颜值）
• 最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。（ABC三维明星）
  

建模步骤

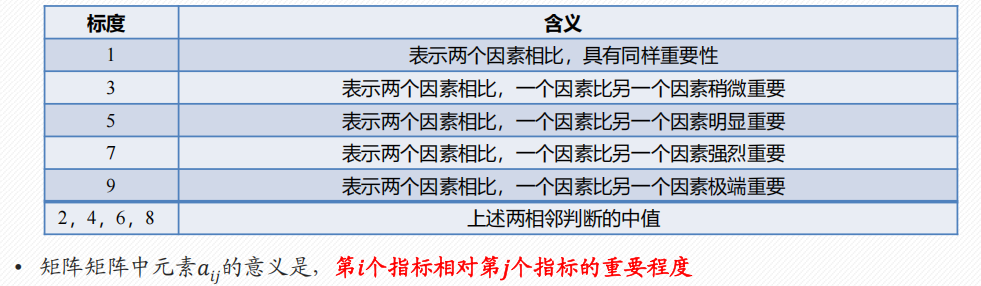
1 建立递阶层次结构模型

2 构造出各层次中的所有判断矩阵

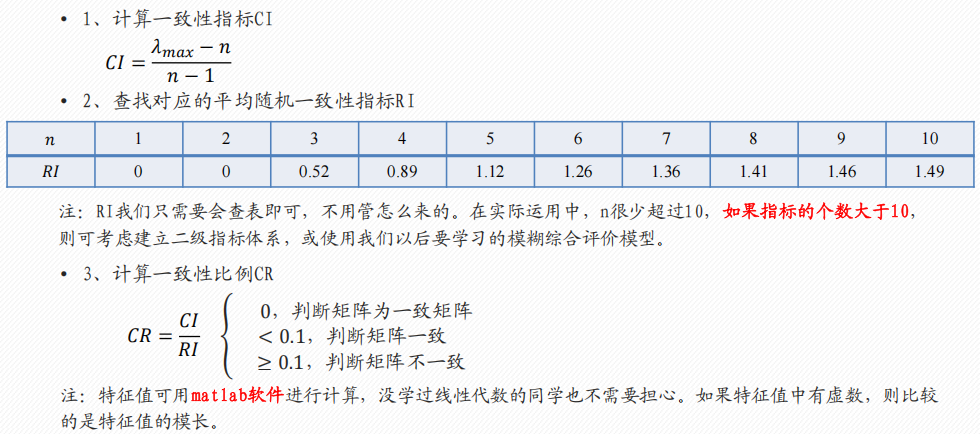
3 一致性检验

4 求权重后进行评价

1.2 优劣解距离法 ( TOPSIS )

基本原理

• 理想解：设想的最优的解(方案)，它的各个属性值都达到各备选方案中的最好的值；
• 负理想解：设想的最劣的解(方案)，它的各个属性值都达到各备选方案中的最坏的值。
• 方案排序的规则是把各备选方案与理想解和负理想解做比较，若其中有一个方案最接近理想解，而同时又远离负理想解，则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择。

建模步骤

将原始矩阵正向化

将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标（越大越好）。

正向矩阵标准化

标准化的方法有很多种，其主要目的就是去除量纲的影响,保证不同评价指标在同一数量级，且数据大小排序不变。

层次分析法 熵权法

计算得分并归一化

1.3 熵权法 ( Entropy_Methord )

• 可用来求权重，较为客观：TOPSIS

基本原理

• 熵权法是一种客观的赋权方法，它可以靠数据本身得出权重。
• 依据的原理：指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。

建模步骤

正向化矩阵（参考TOPSIS）正向化矩阵

正向矩阵标准化

计算概率矩阵

计算熵权

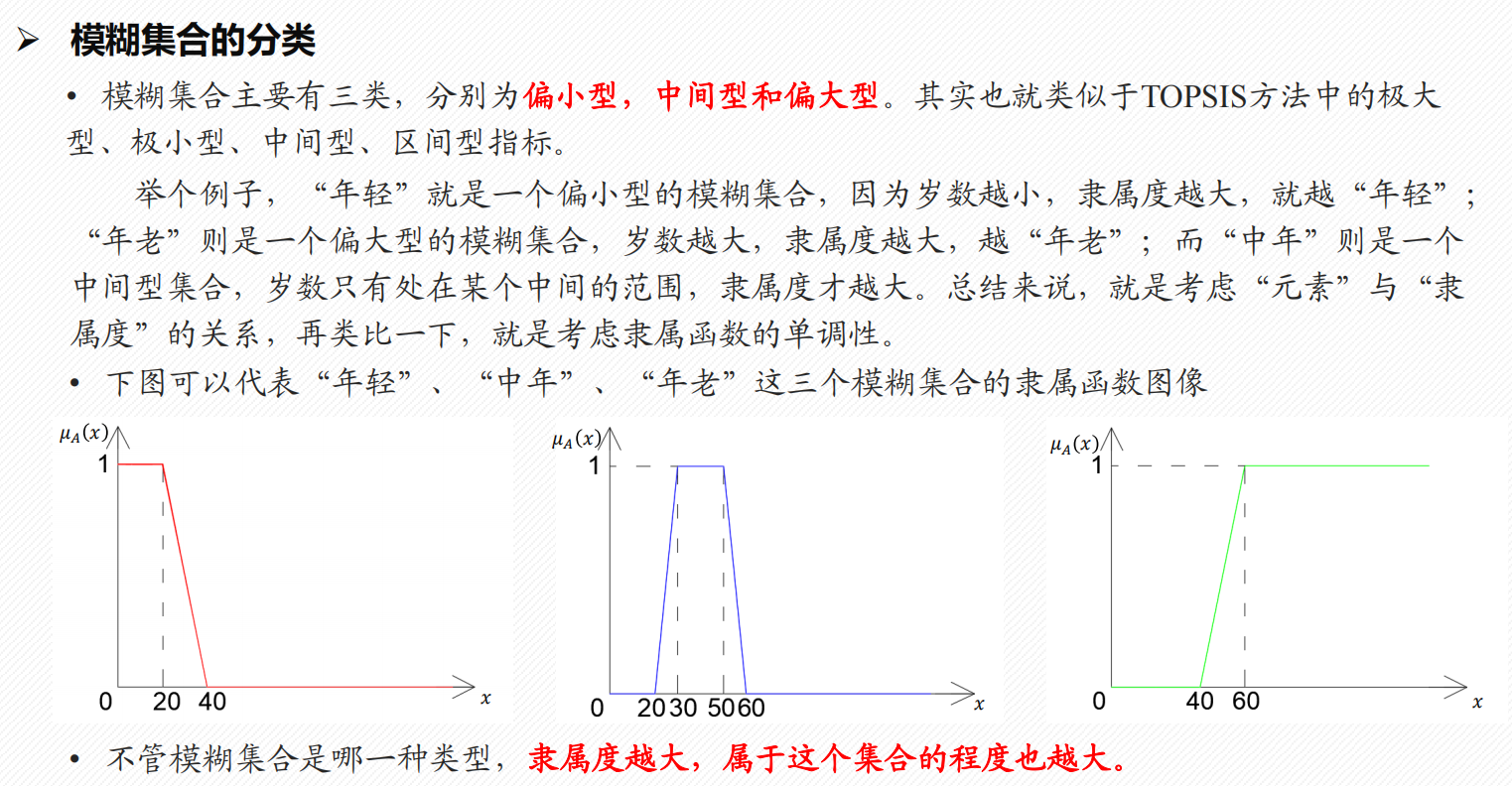
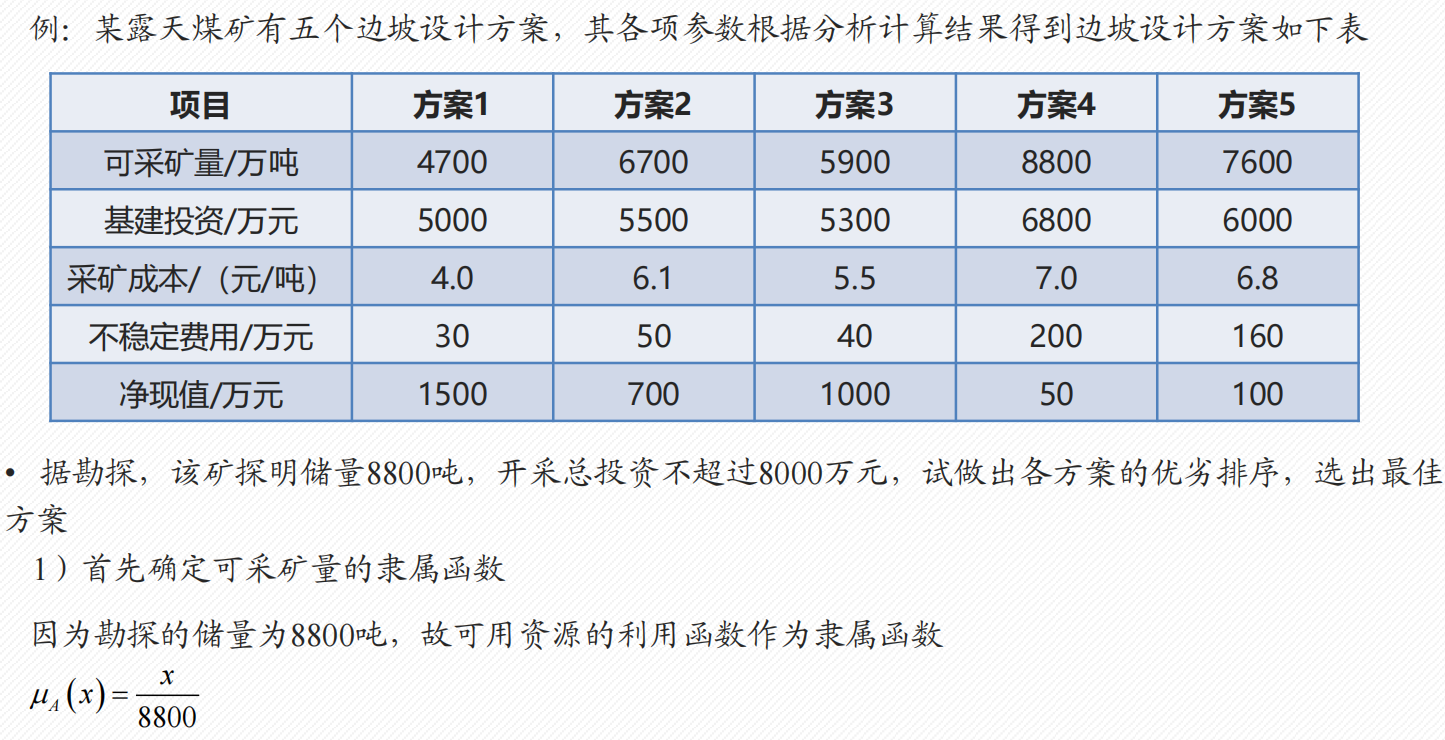
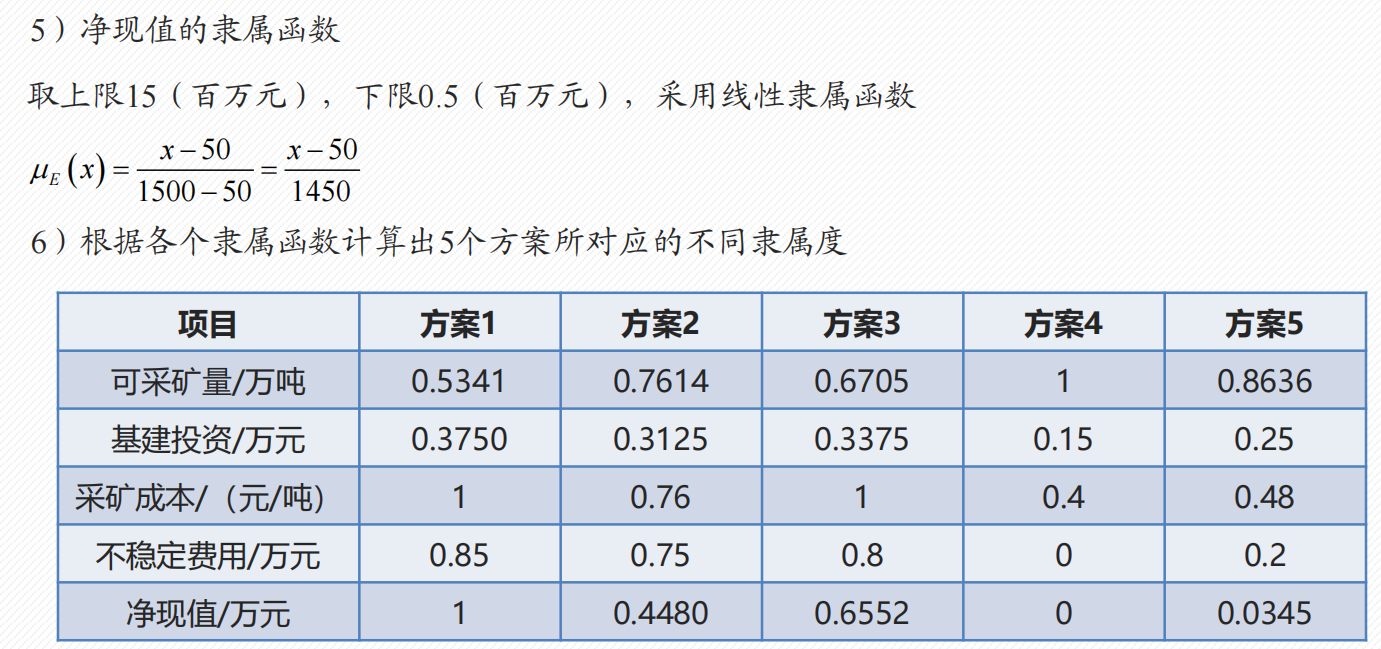
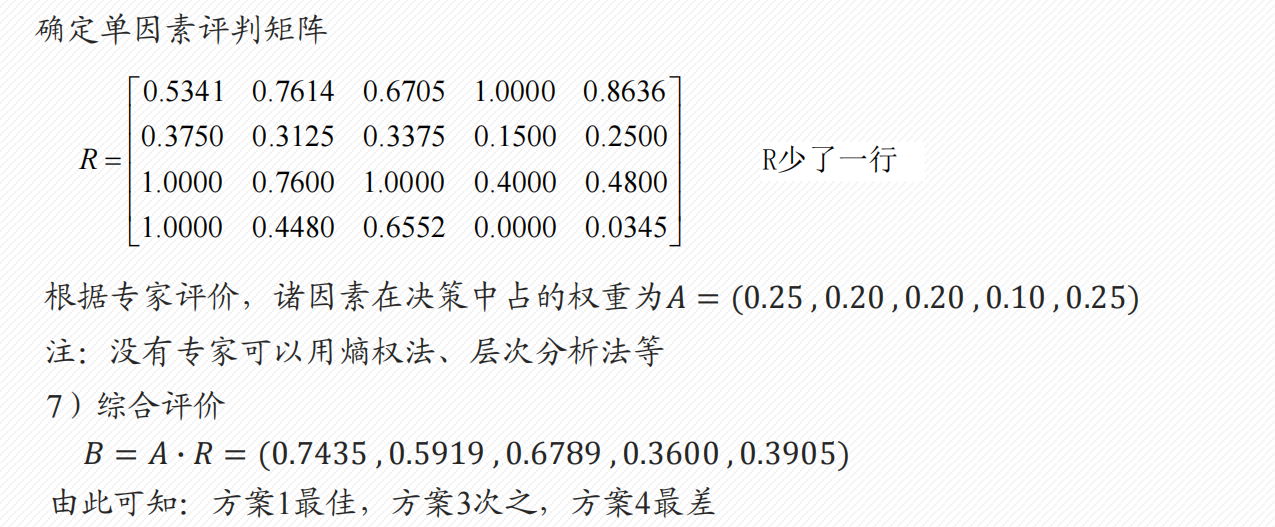
1.4 模糊综合评价

• 适合评判依据模糊

基本原理

一级模糊综合评价模型

模糊统计法

指派法

多层次模糊综合评价模型

1.5 灰色关联分析

• 适合信息不完全

基本原理

• 灰色系统：信息不完全
  • 系统因素不完全明确
  • 因素关系不完全清楚
  • 系统的结构不完全知道
  • 系统的作用原理不完全明了
• 关联分析：所谓关联分析，就是系统地分析因素。回答的问题是：某个包含多种因素的系统中，哪些因素是主要的，哪些是次要的；哪些因素影响大，哪些因素影响小；哪些因素是明显的，哪些因素是潜在的；哪些是需要发展的，那些需要抑制
  

建模步骤

• 灰色关联分析（例题1）
• 灰色关联评价（例题2 K找对象）

1.6 主成分分析 ( PCA )

• 用于变量太多时，对于原先提出的所有变量，将重复的变量（关系紧密的变量）删去，建立尽可能少的新变量，使得这些新变量是两两不相关的，且这些新变量在反映课题的信息方面尽可能保持原有的信息。

基本原理

• 设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上用来降维的一种方法。
• 主要目标是将特征维度变小，同时尽量减少信息损失。就是对一个样本矩阵，
  • 一是换特征，找一组新的特征来重新标识；
  • 二是减少特征，新特征的数目要远小于原特征的数目。
• 几何意义可以理解为旋转坐标系

建模步骤

8) 解释主成分

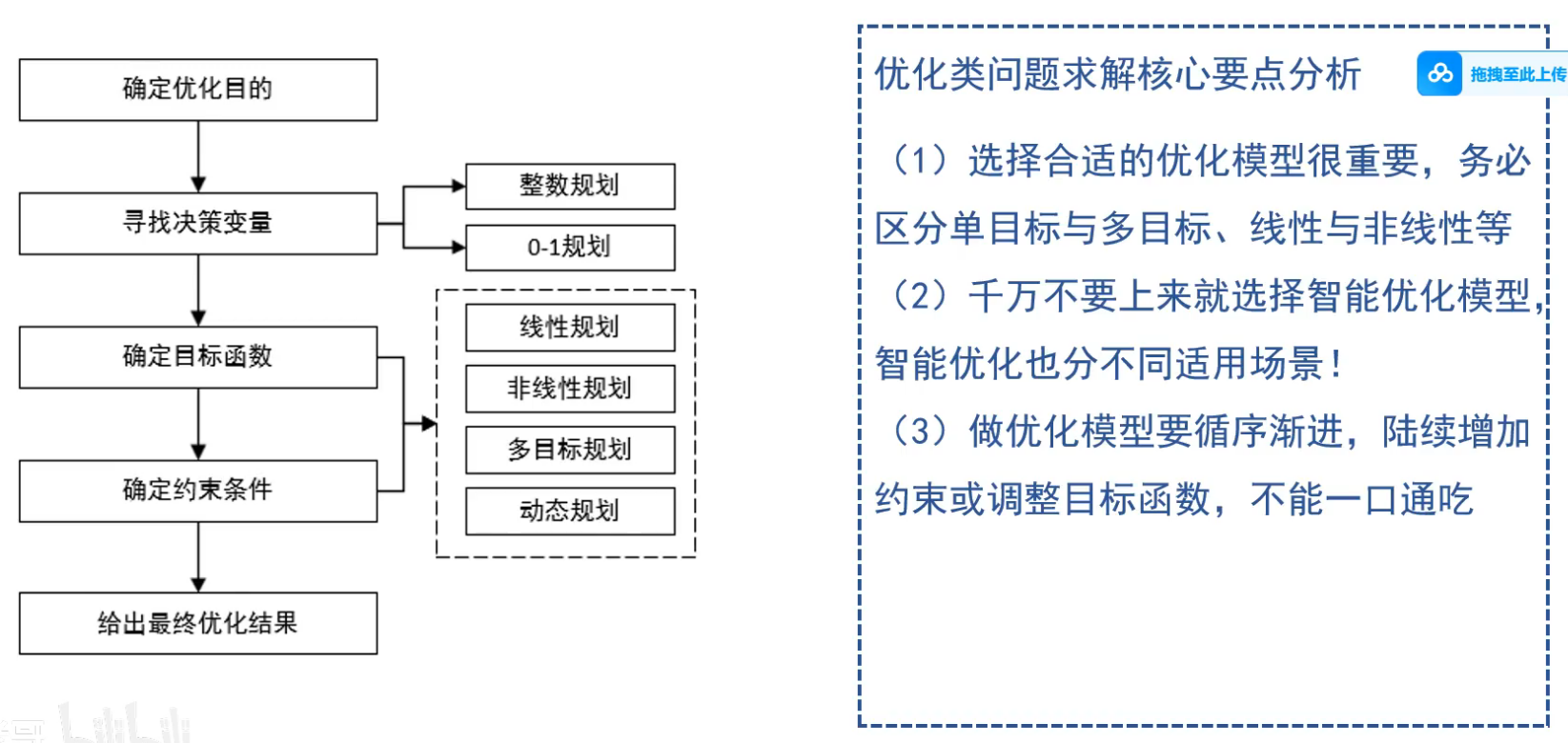
2 运筹优化类

找最大/最小/极值

2.1 线性规划法

• 线性规划法：研究线性约束条件下线性目标函数的极值问题的数学理论和方法。

• 要解决的问题是优化类的（即在有限的资源条件下，获取最大的收益）

• 目标函数和约束条件都是决策变量的线性函数，即不存在 , , , , 等

• 线性规划模型：在一组线性约束条件下，求线性目标函数的最大值或最小值

• 多目标规划：把其中一个目标转化为约束条件进行求解

建模步骤

线性规划的表现形式

关于python代码

2.2 蒙特卡罗法

• 定义：蒙特卡罗法又称统计模拟法，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法，是使用随机数（或更常见伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。
• 是一种思想而不是算法，没有固定的代码
• 非线性规划用蒙特卡罗法求初始值是最精确的

2.3 非线性规划法

1 matlab

例1

%% code1.m
%% 非线性规划的函数
% [x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlfun,option)
% x0表示给定的初始值（用行向量或者列向量表示），必须得写
% A b表示线性不等式约束
% Aeq beq 表示线性等式约束
% lb ub 表示上下界约束
% fun表示目标函数
% nonlfun表示非线性约束的函数
% option 表示求解非线性规划使用的方法
clear;clc
format long g %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）

%% 例题1的求解
% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
% s.t. -(x1-1)^2 +x2 >= 0 ; 2x1-3x2+6 >= 0
x0 = [0 0]; %任意给定一个初始值
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1) % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下
fval = -fval

%% 使用其他算法对例题1求解
% Matlab默认使用的算法是'interior-point' 内点法
% 使用interior point算法 （内点法）
option = optimoptions('fmincon','Algorithm','interior-point')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval
% 使用SQP算法 （序列二次规划法）
option = optimoptions('fmincon','Algorithm','sqp')
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)
fval = -fval %得到-4.358，远远大于内点法得到的-1,猜想是初始值的影响
% 改变初始值试试
x0 = [1 1]; %任意给定一个初始值
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option) % 最小值为-1，和内点法相同（这说明内点法的适应性要好）
fval = -fval

%% 使用蒙特卡罗的方法来找初始值(推荐）
clc,clear;
n=10000000; %生成的随机数组数
x1=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x1
x2=unifrnd(-100,100,n,1); % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x2
fmin=+inf; % 初始化函数f的最小值为正无穷（后续只要找到一个比它小的我们就对其更新）
for i=1:n
x = [x1(i), x2(i)]; %构造x向量, 这里千万别写成了：x =[x1, x2]
if ((x(1)-1)^2-x(2)<=0) & (-2*x1(i)+3*x2(i)-6 <= 0) % 判断是否满足条件
result = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ; % 如果满足条件就计算函数值
if result < fmin % 如果这个函数值小于我们之前计算出来的最小值
fmin = result; % 那么就更新这个函数值为新的最小值
x0 = x; % 并且将此时的x1 x2更新为初始值
end
end
end
disp('蒙特卡罗选取的初始值为：'); disp(x0)
A = [-2 3]; b = 6;
[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)
fval = -fval

%% fun1.m
function f = fun1(x)
% 注意：这里的f实际上就是目标函数，函数的返回值也是f
% 输入值x实际上就是决策变量，由x1和x2组成的向量
% fun1是函数名称，到时候会被fmincon函数调用, 可以任意取名
% 保存的m文件和函数名称得一致，也要为fun1.m
% min f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2
f = x(1)^2+x(2)^2 -x(1)*x(2)-2*x(1)-5*x(2) ;
end

%% nonlfun1.m
function [c,ceq] = nonlfun1(x)
% 注意：这里的c实际上就是非线性不等式约束，ceq实际上就是非线性等式约束
% 输入值x实际上就是决策变量，由x1和x2组成的一个向量
% 返回值有两个，一个是非线性不等式约束c，一个是非线性等式约束ceq
% nonlfun1是函数名称，到时候会被fmincon函数调用, 可以任意取名，但不能和目标函数fun1重名
% 保存的m文件和函数名称得一致，也要为nonlfun1.m
% -(x1-1)^2 +x2 >= 0
c = [(x(1)-1)^2-x(2)]; % 千万別写成了: (x1-1)^2 -x2
ceq = []; % 不存在非线性等式约束，所以用[]表示
end

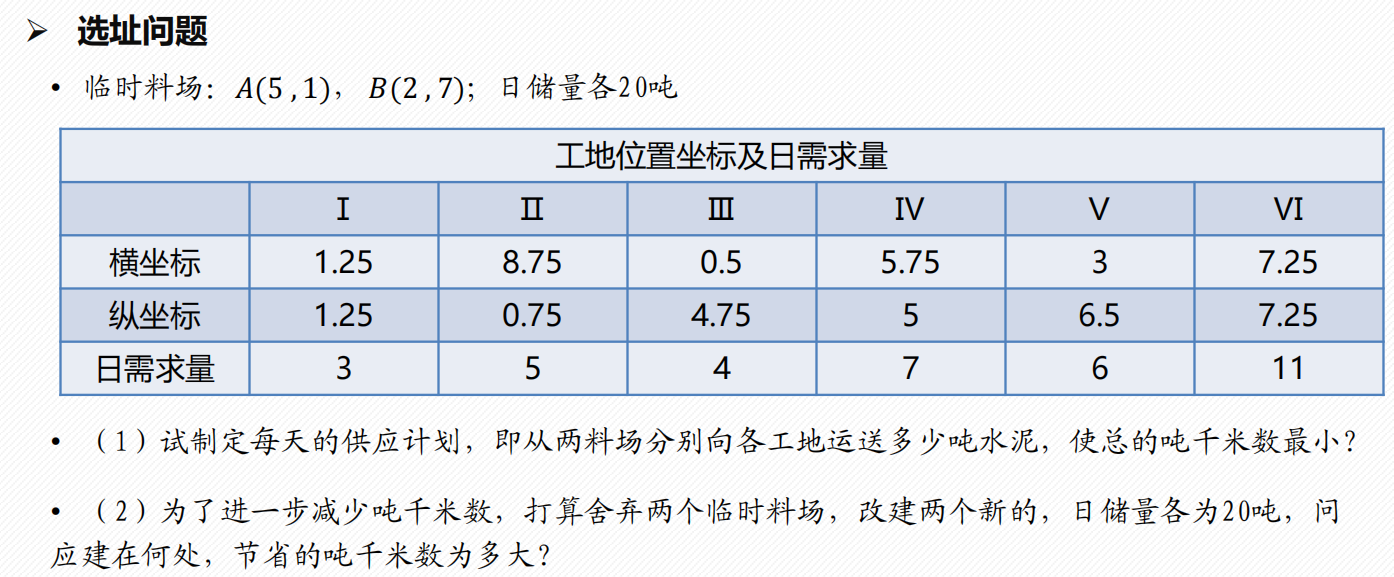
例2

%% xuanzhiwenti.m
%%%第一问：线性规划
clear;clc;
% 6个工地坐标
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
% 临时料场位置
x=[5 2];
y=[1 7];
% 6个工地水泥日用量
d=[3 5 4 7 6 11];
% 计算目标函数系数，即6工地与两个料场的距离，总共12个值
for i=1:6 % 对于6个工地
for j=1:2 % 接收两个料场的供用
l(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2); % 距离
end
end
f = [l(:,1);l(:,2)]; % 目标函数系数向量，总共12个值
% 不等式约束条件的变量系数和常数项
% 双下标转换成单下标：x11=x1，x21=x2，x31=x3，x41=x4，…，x62=x12
A = [1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1];
% 两个临时料场日储量
b = [20;20];
% 矩阵的行数是约束条件个数，列数是变量个数
% 等式约束的变量系数和常数项
Aeq = [eye(6),eye(6)]; % 两个单位矩阵横向拼成
beq=[d(1);d(2);d(3);d(4);d(5);d(6)];
% 所有变量下限全是0
Vlb=[0 0 0 0 0 0 0 0 0 0 0 0];
[x,fval]=linprog(f,A,b,Aeq,beq,Vlb);
x,fval

%% 第二问：非线性规划
% 注意！第二问中求新料场位置，所以两个料场的横纵坐标也是变量，所以多了4个变量
% 对新坐标没有不等式约束，所以其不等式约束条件里的系数为0
A2 = [1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B2 = [20;20];
% 对新坐标也没有等式约束，所以相应项也为0
Aeq2 = [eye(6),eye(6),zeros(6,4)]; % 两个单位矩阵和一个全0矩阵拼成
beq2=[3 5 4 7 6 11]';
Vlb2=[zeros(12,1);-inf;-inf;-inf;-inf];
% 非线性规划必须赋初值，可以基于问题情况来设，或设置rand()随机数等等；
% 初始值设为线性规划的计算结果，即临时料场的坐标
% 设置初始值x0，此处可直接使用第一问的值作为初始值；
x0=[3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7]';
[x2,fval2]=fmincon(@fun2,x0,A2,B2,Aeq2,beq2,Vlb2)
% 若约束条件里有非线性函数，可使用在fmincon里使用nonlcon 项
% 若有条件，可使用蒙特卡罗法求一个近似解作为初始值
% 1、因为第2问模型中有16个变量，所以要给16个变量分别生成随机值，作为当前解；
% 2、判断这些当前解是否满足模型的约束条件
% 3、若满足，代入目标函数，求当前目标函数值
% 4、判断当前目标函数值是否比已求的较优函数值更好，若是，则替换掉较优函数值和对应的较优解
% 5、不断重复前5步，构成统计意义，求得较优解。
p0 = 10000; n = 10^6; tic
x_m0 = 0;
for i = 1:n
% 前12个数是6个工地从两个料场接收的量，6个工地分别需要3,5,4,7,6,11吨水泥
% 所以前12个变量分别需要取0到3，0到5，……，0到11的随机数
% 为加速求近似，取前12个变量（工地从料场接受的量）为随机整数
% randi(n)为随机取1到n之间的一个整数，则randi(n+1)-1为取0到n间随机整数
% 后4个变量是两个料场的横纵坐标，取一定范围内的随机数（根据题目，工地坐标都在0到9，所以此处取0到9）
% ...表示续行，即下一行和这行是在同一行
x_m = [randi(4)-1,randi(6)-1,randi(5)-1,randi(8)-1,randi(7)-1,randi(12)-1,...
randi(4)-1,randi(6)-1,randi(5)-1,randi(8)-1,randi(7)-1,randi(12)-1,...
9*rand(1,4)];
[g,k] = constraint(x_m); % 约束条件
if all(g<=0) % 等式约束难以严格满足，所以此处相差不大即可算近似
if all(abs(k)<=1)
ff = fun2(x_m); % 目标函数
if ff<p0
x_m0 = x_m; p0 = ff;
end
end
end
end
x_m0,p0,toc
% 以采样10^6次的蒙特卡罗法求得的近似值作为初始值，调用fmincon
[x3,fval3]=fmincon(@fun2,x_m0,A2,B2,Aeq2,beq2,Vlb2)
% 此时最终求得的结果fval3 = 85.4054，
% 优于前面以第一问线性规划结果为初始值时求得的90.4920
% 注意！！！非线性规划每次求解的结果都不一样！！！
% 多次运行相同代码，得出的结果不相同是正常的！！！

%% constraint.m
function [g,k] = constraint(x)
% 不等式约束条件
% sum(x(:,1:6),2)是对矩阵前6列按行求和，即对前6个元素求和，
% 对应6个工地接收第一个料场的总量。再减去20，即把不等式右边常数项移到左边
g = [sum(x(:,1:6),2)-20
sum(x(:,7:12),2)-20
];
% 等式约束条件,6个工地从两个料场收到的总量分别为3,5,4,7,6,11
k = [x(1)+x(7)-3
x(2)+x(8)-5
x(3)+x(9)-4
x(4)+x(10)-7
x(5)+x(11)-6
x(6)+x(12)-11
];
end

%% fun2.m
function ff = fun2(x)
% 6个工地坐标
a1 = [1.25 8.75 0.5 5.75 3 7.25];
b1 = [1.25 0.75 4.75 5 6.5 7.75];
f1=0;
% x(13)是第一个新料场的横坐标，x(14)是其纵坐标；
% x(15)是第二个新料场的横坐标，x(16)是其纵坐标；
for i=1:6
s(i)=sqrt((x(13)-a1(i))^2+(x(14)-b1(i))^2); % 第一个料场到各工地的距离
f1=s(i)*x(i)+f1; % 第一个料场给各工地的吨千米数
end
f2=0;
for i=7:12
s(i)=sqrt((x(15)-a1(i-6))^2+(x(16)-b1(i-6))^2); % 第二个料场到各工地的距离
f2=s(i)*x(i)+f2; % 第二个料场给各工地的吨千米数
end
% 总运输量（吨千米数）
ff=f1+f2;
end

2 python

2.4 整数规划和0-1规划

• 在整数规划中，如果所有变量都限制为整数，则称为纯整数规划；
• 如果仅一部分变量限制为整数，则称为混合整数规划。
• 整数规划的一种特殊情形是0-1规划，它的变数仅限于0或1。
  

1 matlab

2 python

2.5 最大最小化规划模型 ( Minimax )

• 最大最小化：最小化最坏情况
• 最大最小算法（Minimax算法），是一种找出失败的最大可能性中的最小值的算法(即最小化对手的最大得益)。在实际问题中也有许多求最大值的最小化问题，例如急救中心选址问题就是要规划其到所有地点最大距离的最小值，在投资规划中要确定最大风险的最低限度等，为此，对每个 ，我们先求出目标值 的最大值，然后再求这些最大值中的最小值。
  

matlab

python

2.6 多目标规划模型

• 多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。
  • 设计一个导弹，既要射程远，命中率高，还要耗燃料少
  • 选择新厂址，除了要考虑运费、造价、燃料供应费等经济指标外，还要考虑对环境的污染等社会因素
• 解题思路
  1. 把目标函数转换成约束条件，多目标转换为单目标
  2. 本节内容

2.7 动态规划

算法还在追我

2.8 图论

matlab画图

2.9 最短路径

单源最短路径
所有结点对的最短路径
matlab直接调用shortestpath

2.10 最小生成树

prim
kruskal
matlab调用minspantree

2.11 启发式算法

• 启发式算法是基于直观或经验构造的算法，在可接受的计算时间和空间条件下，给出待解决优化问题的一个可行解。
• 启发式算法并不保证找到最优解，只是在有限资源下找到还不错的解
• 经典的启发式算法包括模拟退火、遗传算法、蚁群算法、神经网络等。
• 启发式算法的共同的目标：求NP-hard组合优化问题的全局最优解，NP-hard问题的限制它们只能以启发式的算法去求解实际问题。

模拟退火

遗传算法

蚁群算法

3 控制预测类

• 根据已知预测未知
  
  

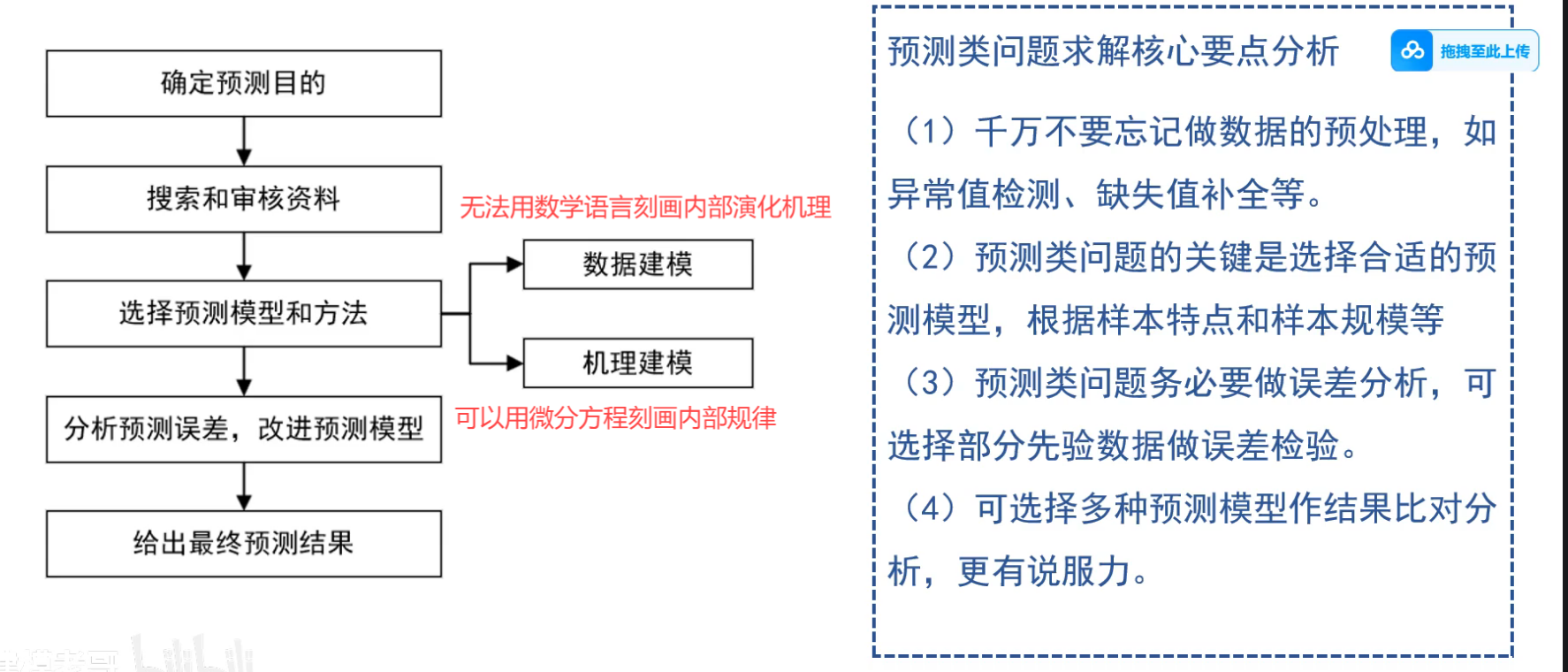
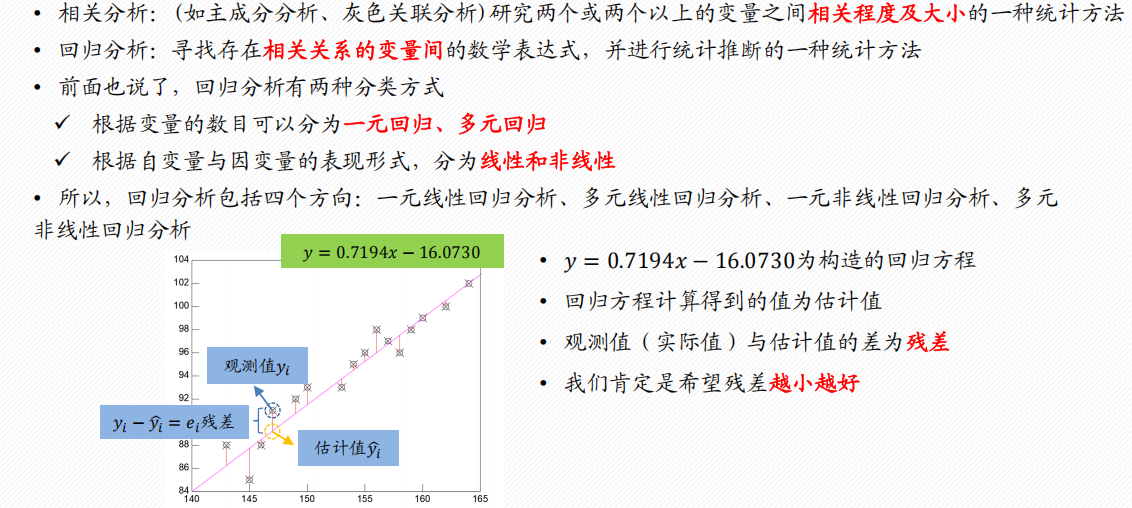
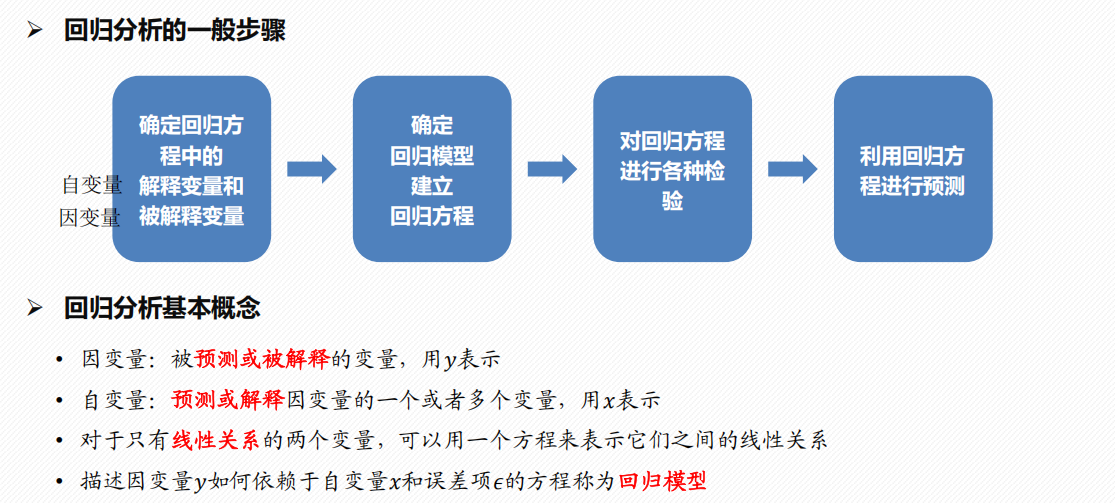
3.1 回归分析概述

回归分析步骤

以一元线性回归为例

确定回归模型、建立回归方程

对回归方程进行各种检验

1. 回归直线的拟合优度+判定系数，看 是否接近1
   
   
2. 显著性检验（线性关系检验+回归系数的显著性检验）
   
   
   

多元回归分析

曲线回归分析

多重共线性

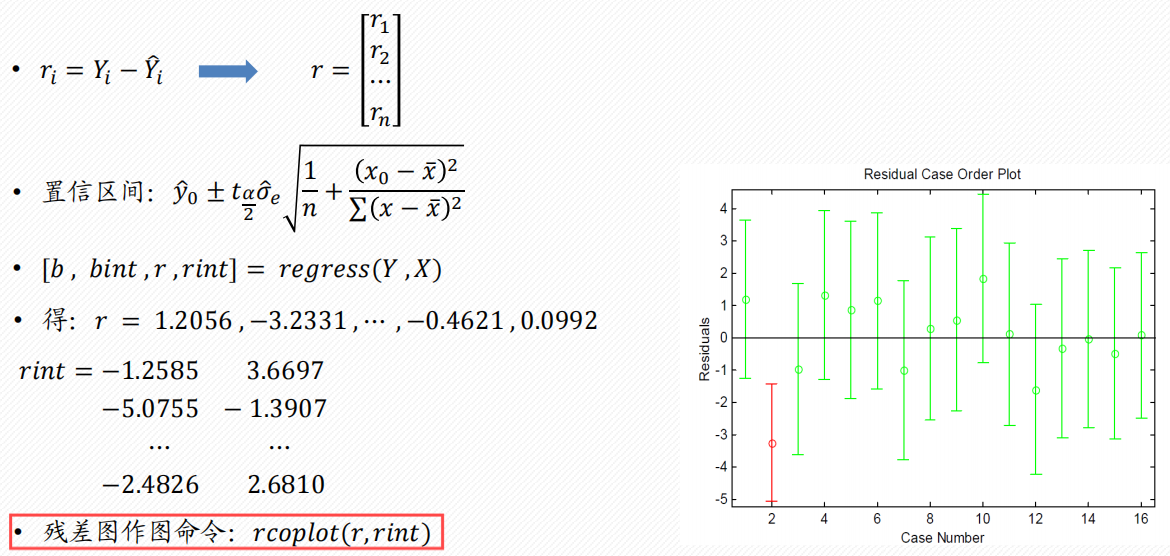
3.2 一元线性回归分析

• 使用 regress 函数
  

• b
  

• bint
  

• r & rint
  

• stats
  
  
  

3.3 多元线性回归分析

理论

步骤

1. 多元线性回归模型的参数估计
   
2. 多元线性回归模型和回归系数的检验
   
3. 多元线性回归模型的预测
   

matlab

调用 regress 函数

逐步回归判断哪个变量影响更大

总结

• 先逐步回归判断哪个变量影响更大，删掉影响小的变量
• 对影响大的变量进行线性回归

3.4 非线性回归分析

1 配曲线求解

例

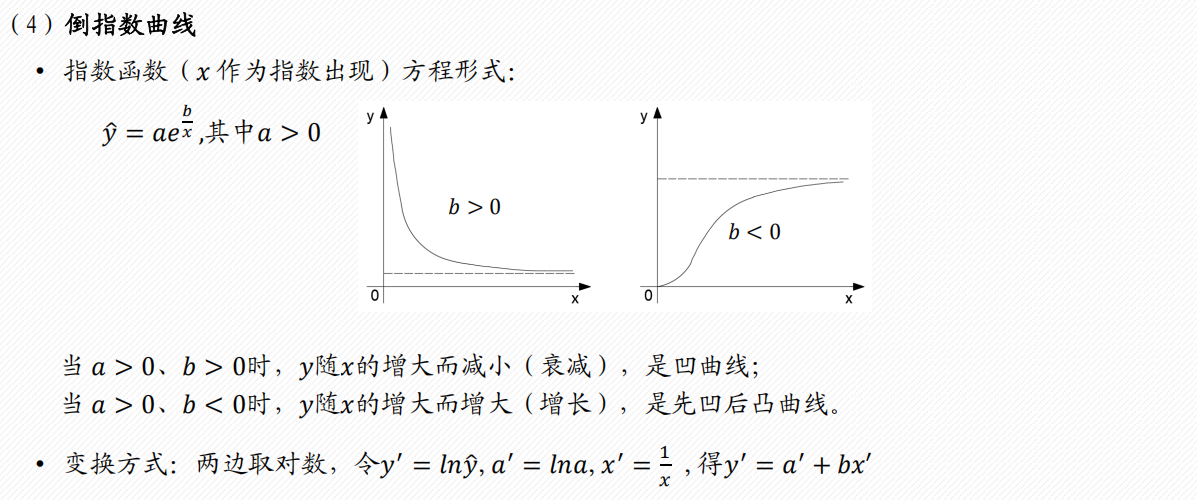
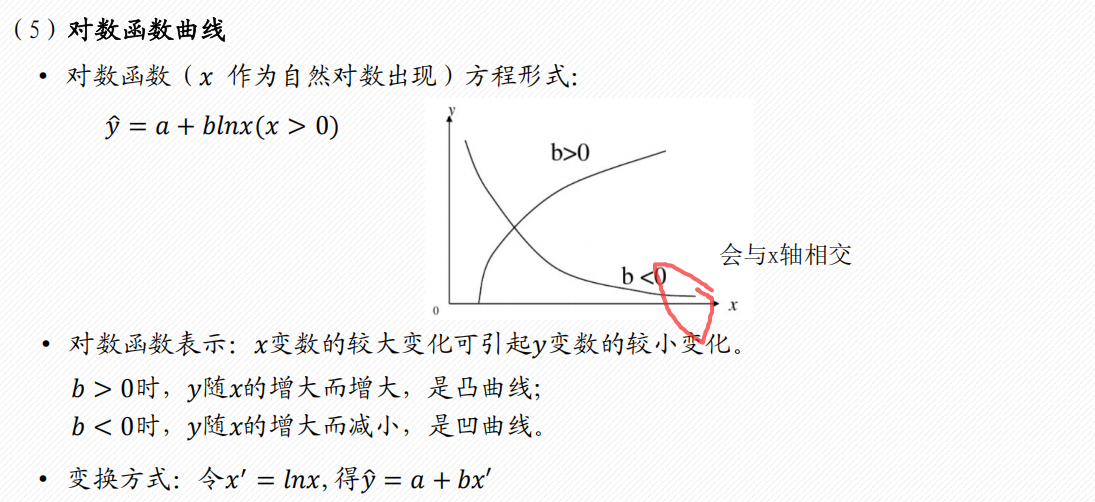
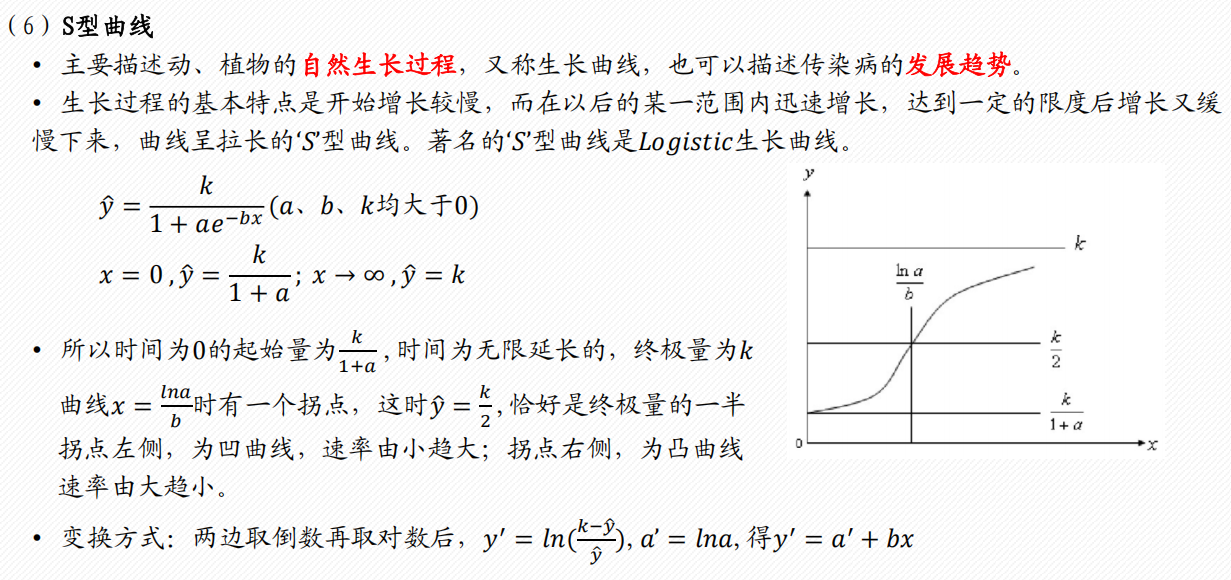
常见的6类曲线

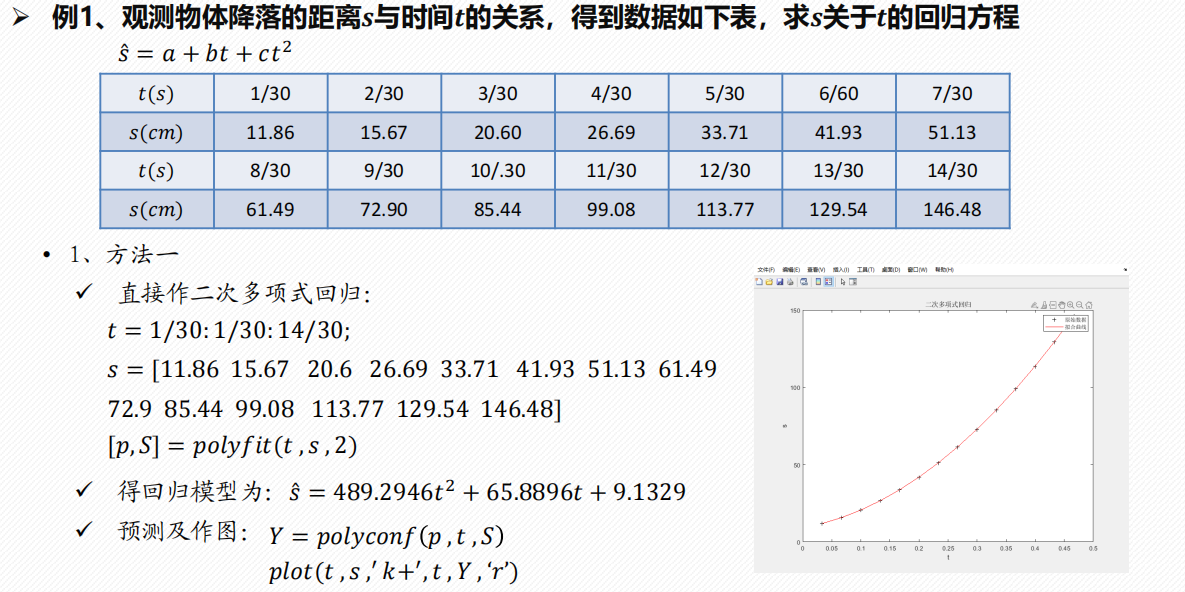
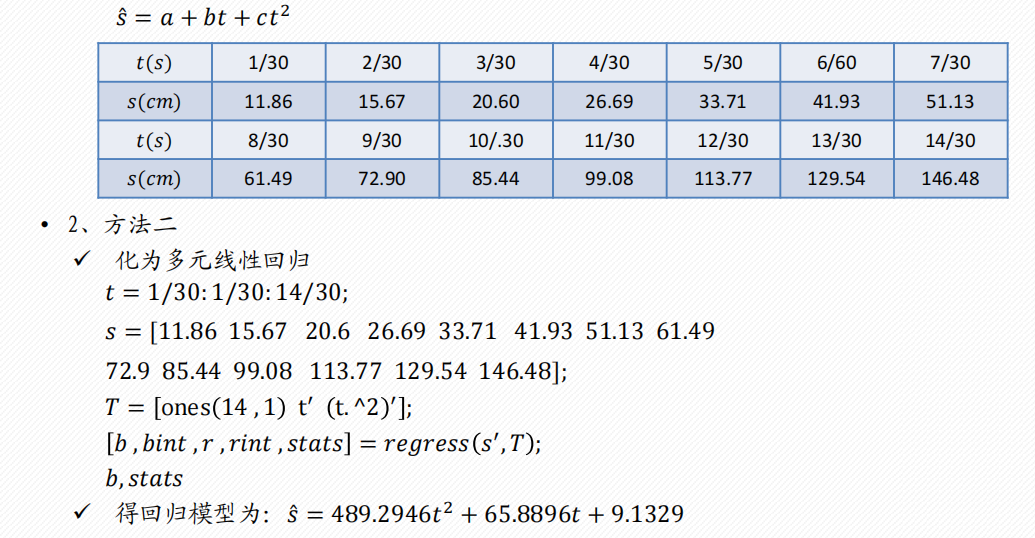
2 多项式回归

一元多项式回归

例

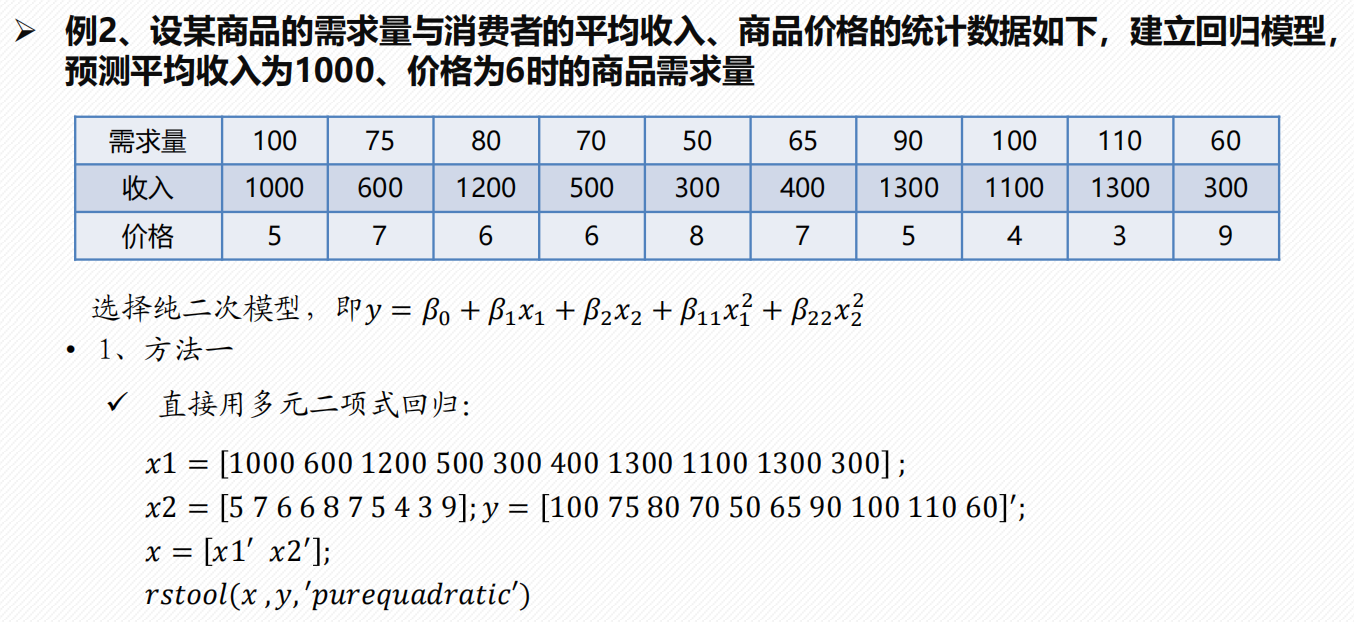
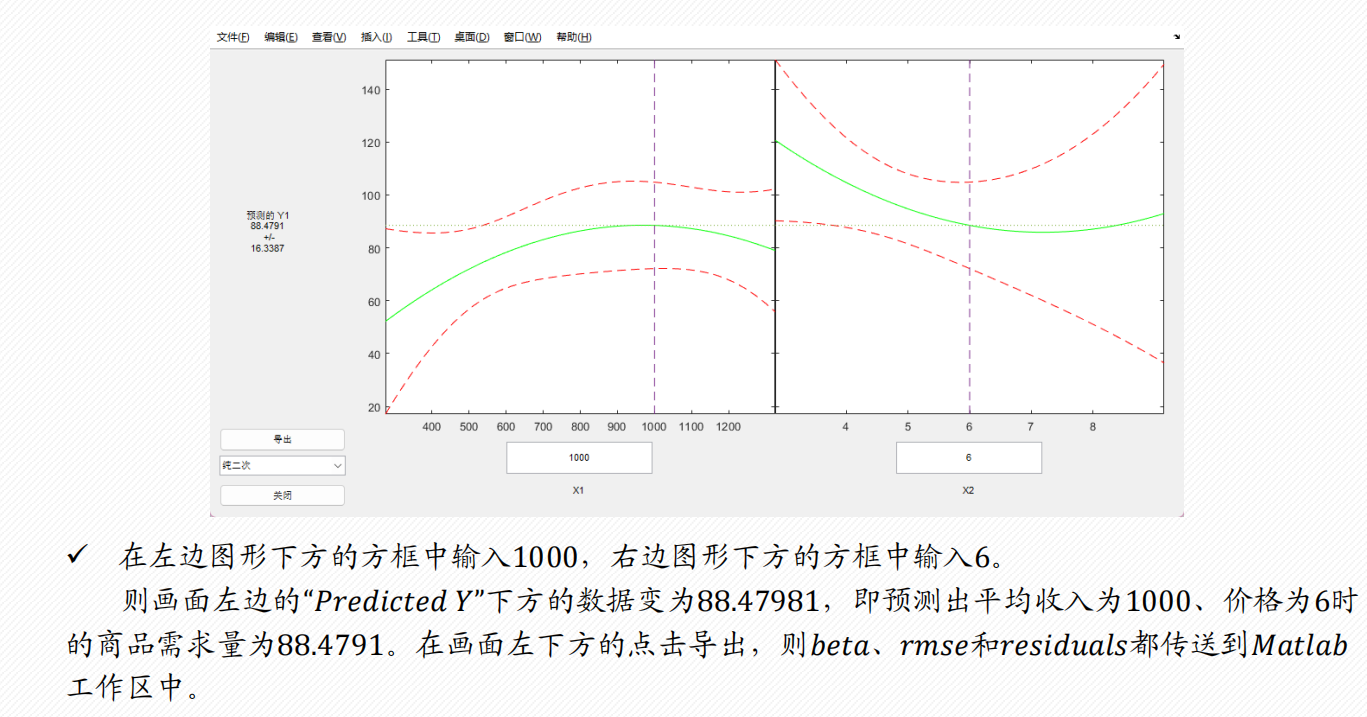
多元二项式回归

例

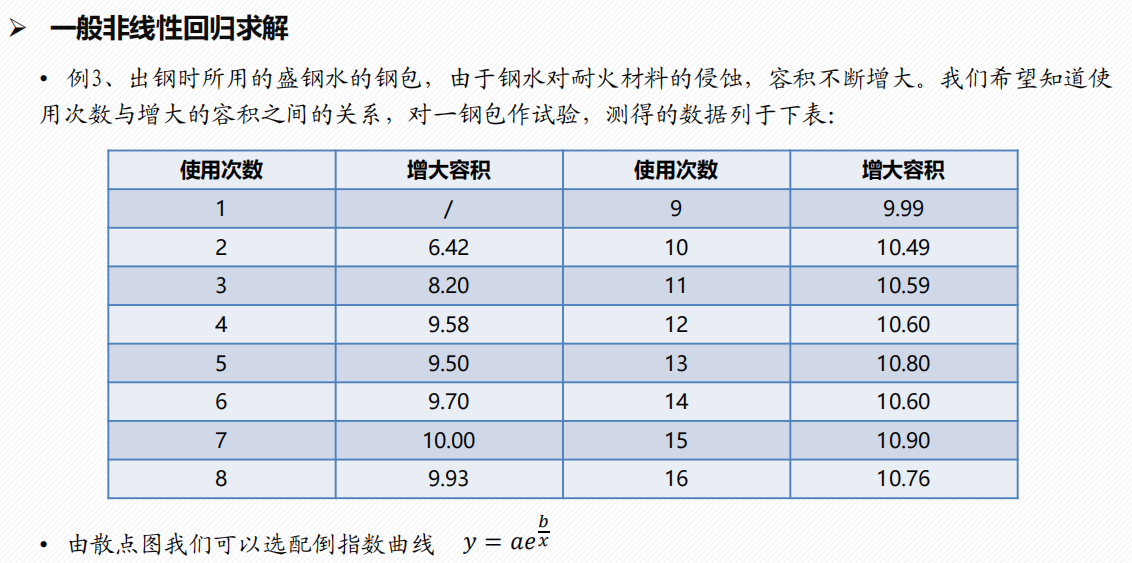
3 一般求解

例

4 其他方法

• 神经网络
• 支持向量机

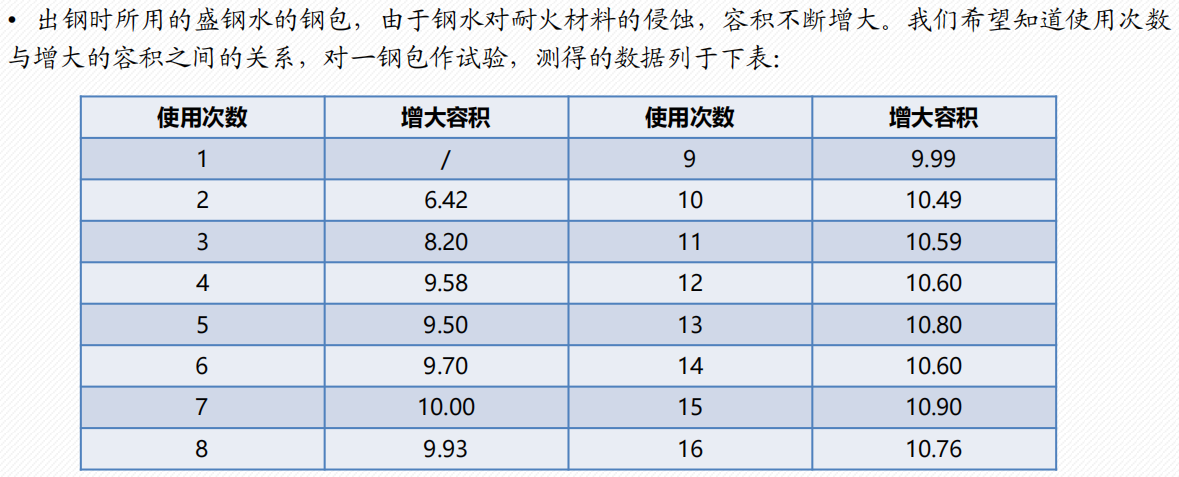
3.5 灰色预测 GM(1, 1)

• 什么是灰色预测？
  所谓灰色预测，就是对既含有已知信息又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。
• 灰色预测适用于什么情况？
  • 数据是以年份度量的非负数据（如果是月份或者季度数据一般要用时间序列模型），比如定时求量的题目，即已知一些年份数据，预测下一年的数据，常见有GDP、人口数量、耕地面积、粮食产量等；或者定量求时，已知一些年份数据和某灾变的阈值，预测下次灾变时间。
  • 数据能经过准指数规律的检验（除了前两期外，后面至少90%的期数的光滑比要低于0.5）。
  • 数据的期数较短且和其他数据之间的关联性不强（小于等于10，也不能太短了，比如只有3期数据），要是数据期数较长，一般用传统的时间序列模型比较合适。
  • 应该是时期时间序列而不是时点时间序列

模型求解

模型检验

模型求解前，判断能否使用灰色预测模型

模型评价

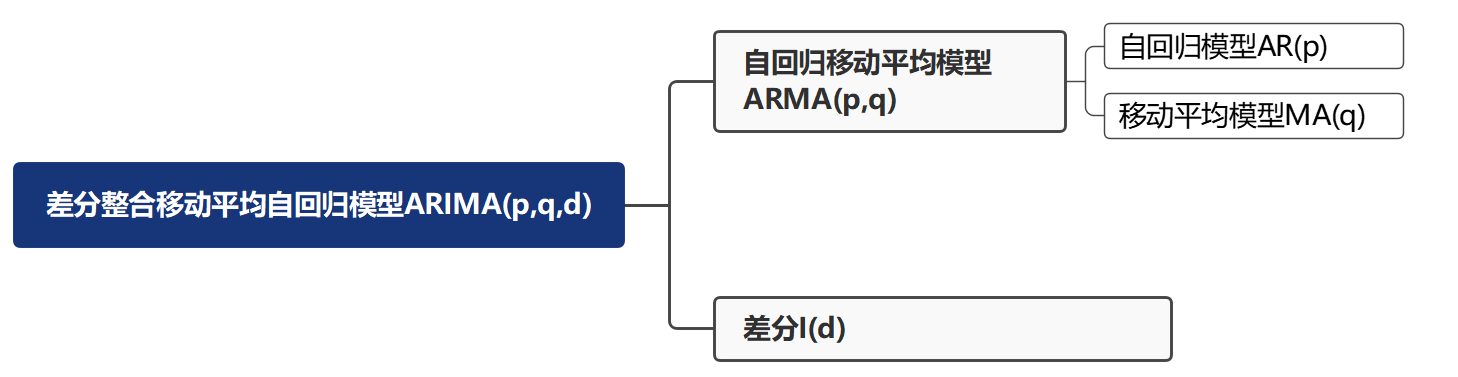
3.6 时间序列模型 ( ARIMA )

时间序列根据时间和数值性质的不同，可以分为时期时间序列和时点时间序列

• 时期序列中，数值要素反映现象在一定时期内发展的结果
• 时点序列中，数值要素反映现象在一定时点上的瞬间水平
• 时期序列可加，时点序列不可加

模型介绍

自回归模型 ( AR(p) )

移动平均模型 ( MA(q) )

自回归移动平均模型 ( ARMA(p, q) )

差分自回归移动平均模型 ( ARIMA(p, d, q) )

建模步骤

1 实现/检验 平稳性

检验平稳性：

• 图检验法
  • 时间序列趋势图
  • 自相关函数图
• ADF 检验

不平稳怎么变平稳：

• 差分法（一般 1-2 次就够）

自相关系数 (ACF) 和偏自相关系数 (PACF)

• 自相关系数
  
• 偏自相关系数：剔除中间 k-1 个随机变量的干扰，只考虑 对 的影响
  

ADF检验

2 确定 p, q, d

• d：差分次数（一般为0, 1, 2）

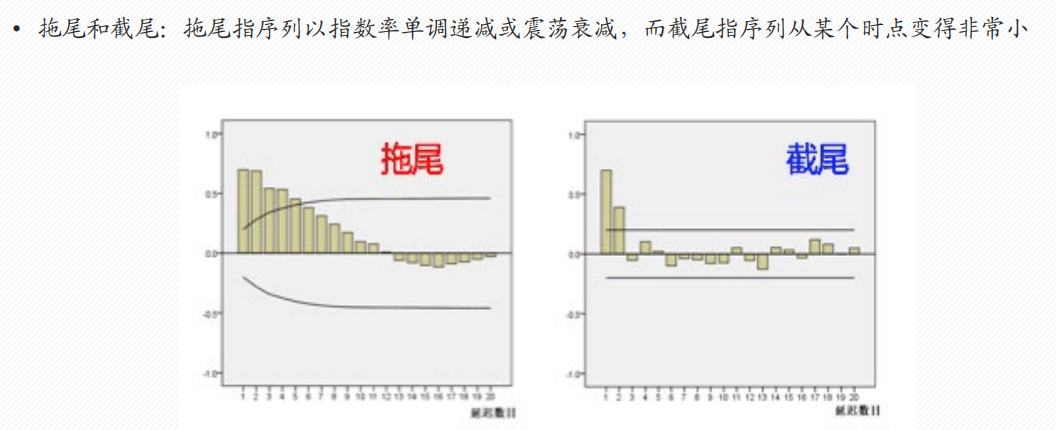
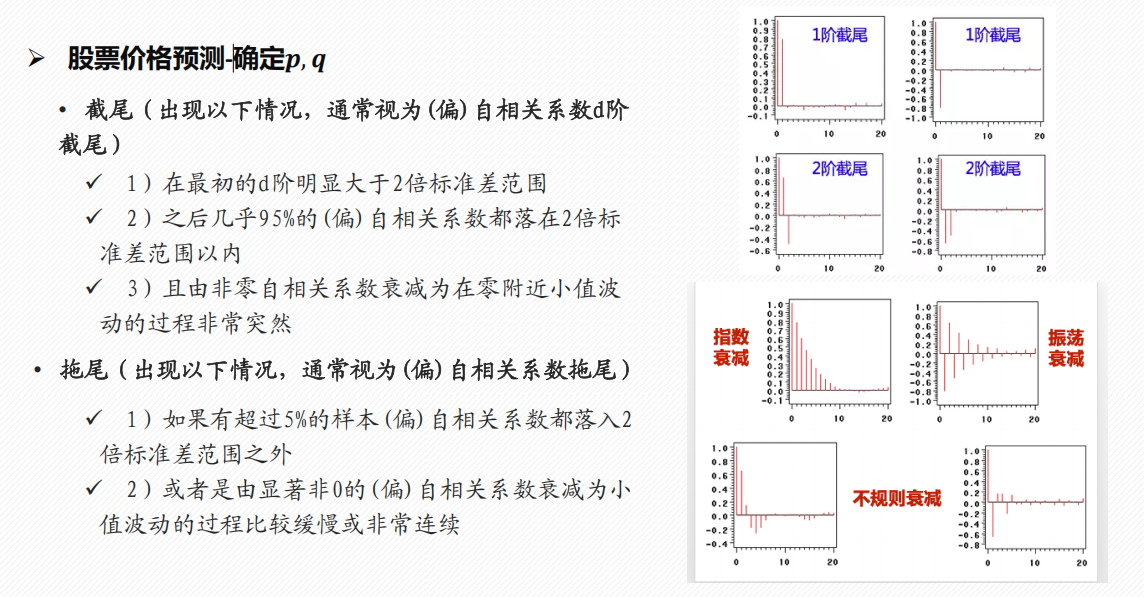
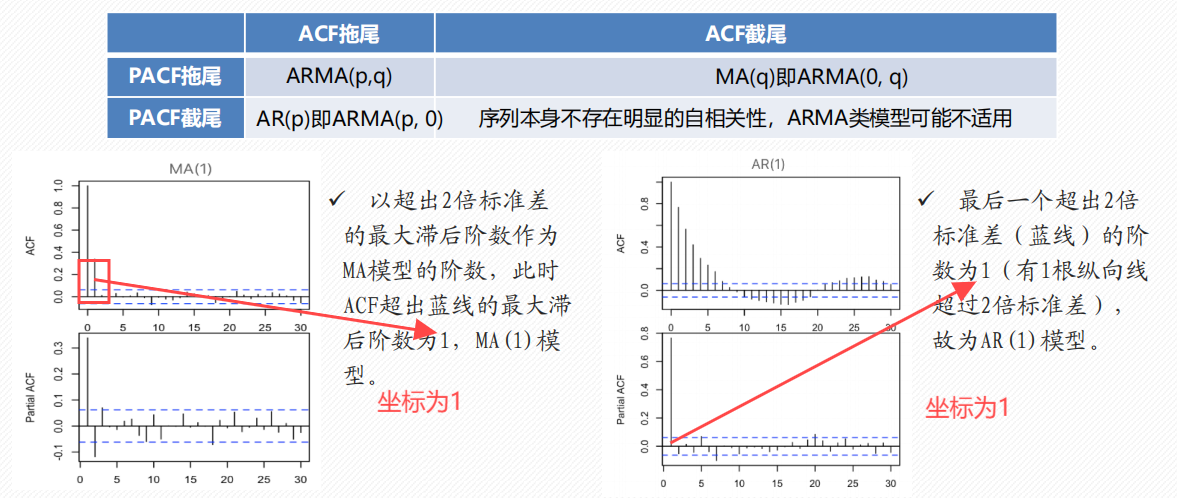
法1：ACF/PACF 截尾/拖尾判断

法2：AIC BIC准则（更客观）

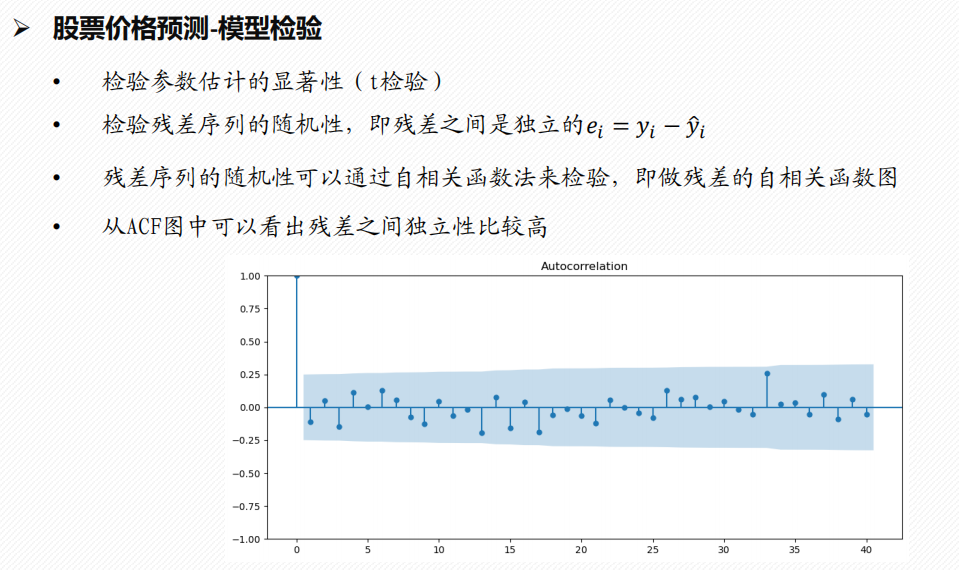
3 模型检验

4 模型预测

4 机理分析类

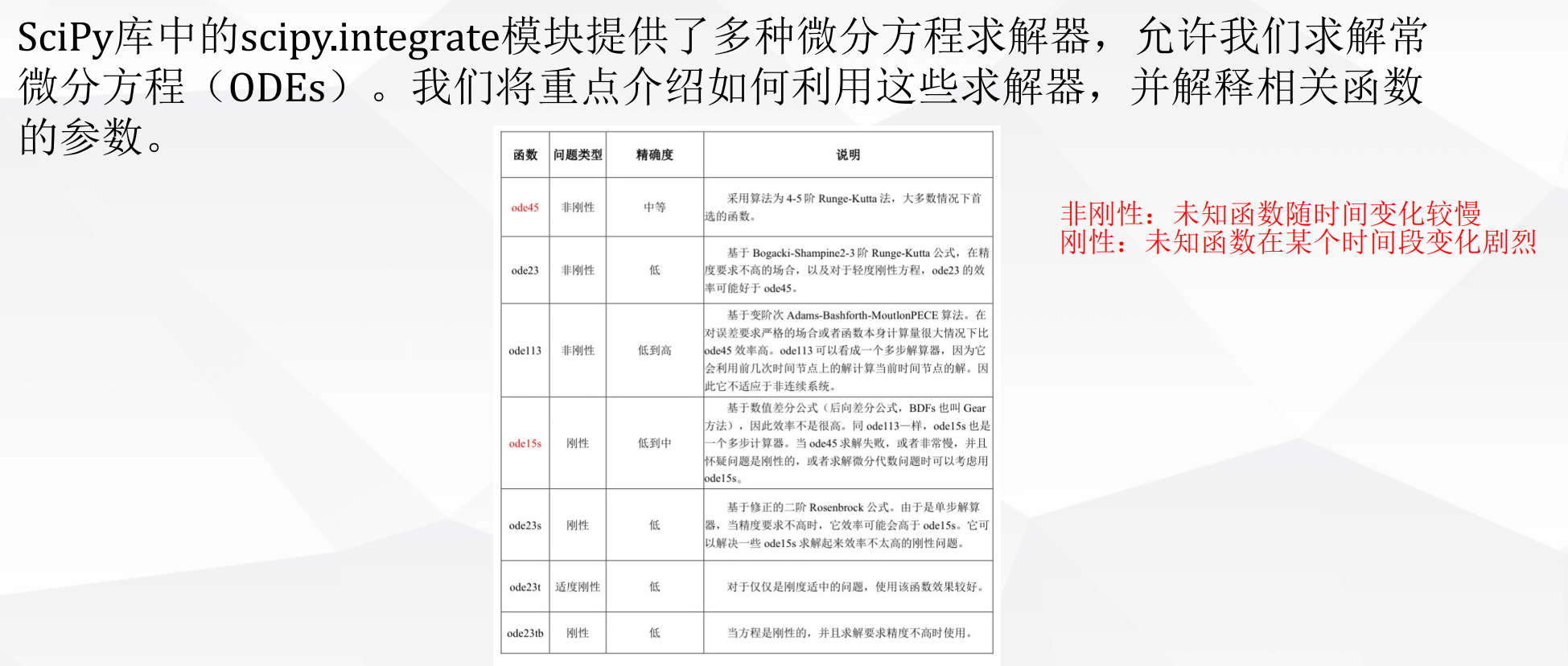
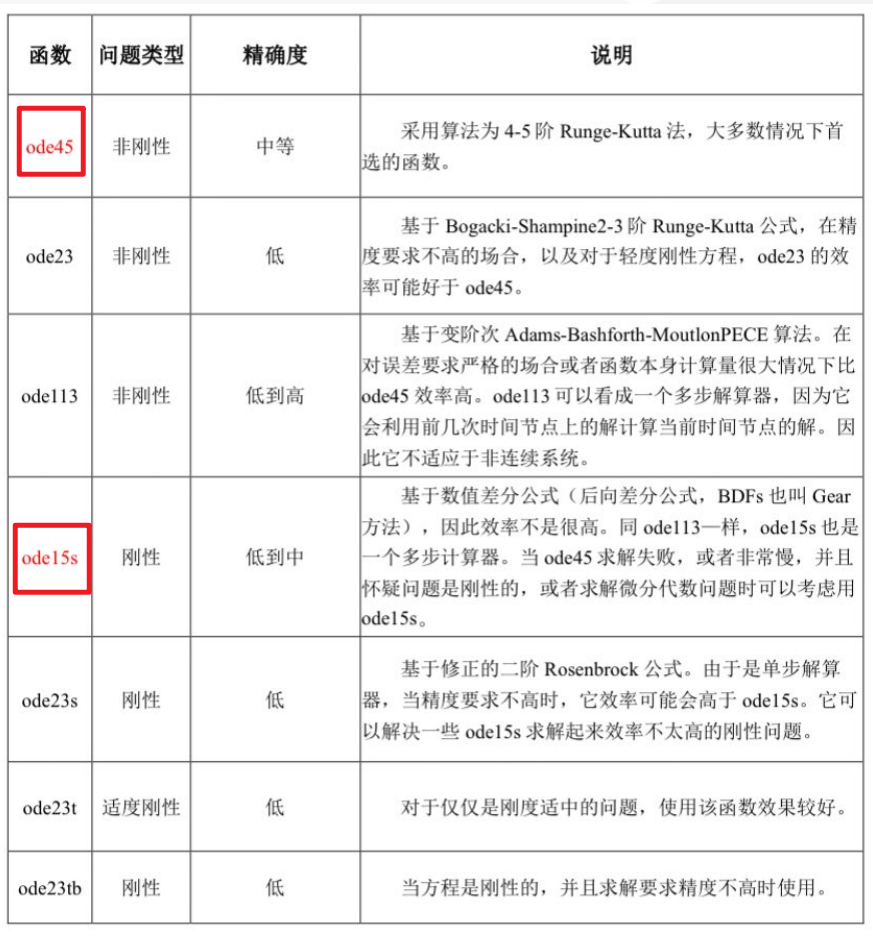
4.1 python求解微分方程

常用ODE求解器： odeint

• 求解简单的微分方程（一阶或二阶）
  

例

import numpy as np  
from matplotlib import pyplot as plt  
from scipy.integrate import odeint  
  
def model(y, t):  
    k = 0.3  
    dydt = -k*y  
    return dydt  
  
y0 = 5  
t = np.linspace(0, 20, 100)  
result = odeint(model, y0, t)  
print(result)  
plt.plot(t, result)  
plt.show()

solve_ivp 函数

例

import numpy as np  
from matplotlib import pyplot as plt  
from scipy.integrate import solve_ivp  
  
def model(t, y):  
    k = 0.3  
    dydt = -k*y  
    return dydt  
  
y0 = [5]  
t_span = [0, 20]  
t_eval=np.linspace(0, 20, num=100)  
sol = solve_ivp(model, t_span, y0, t_eval = t_eval)  
  
print(sol.y)  
plt.plot(sol.t, sol.y[0])  
plt.show()

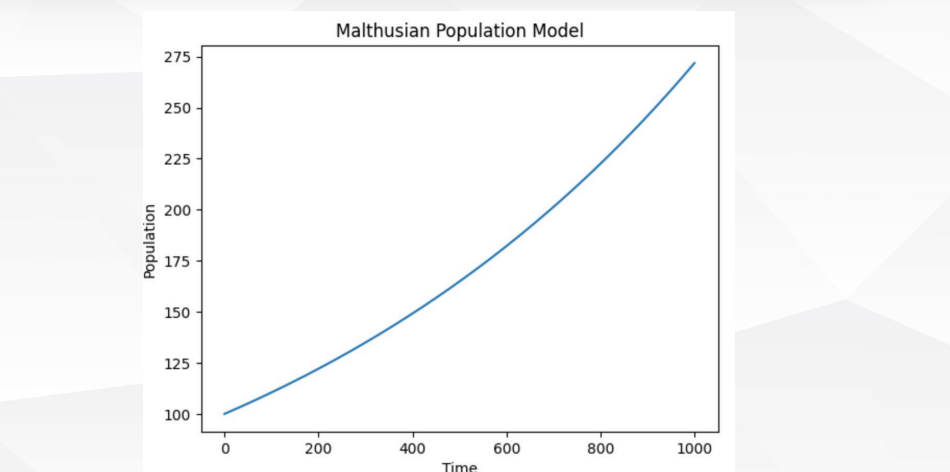
4.2 马尔萨斯人口模型

背景

建模与求解

模型评价

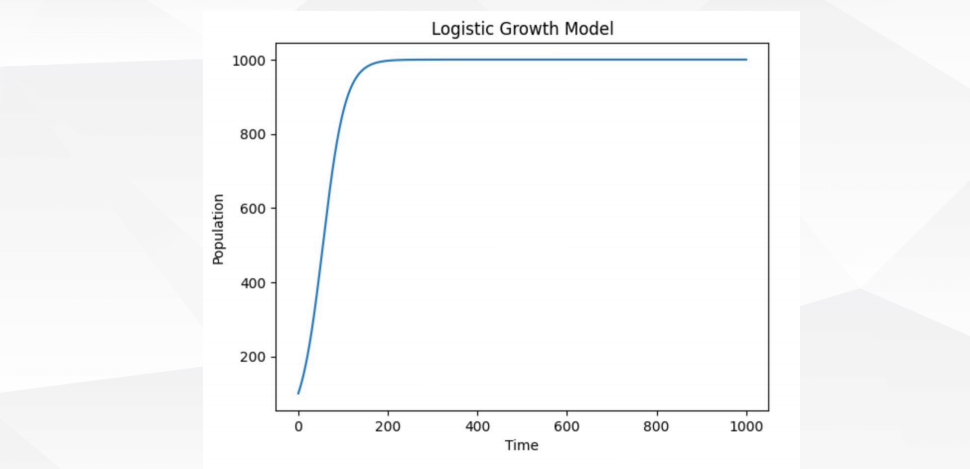
4.3 阻滞增长模型（接上文）

背景

建模与求解

模型评价

4.4 Volterra模型（沃尔泰拉模型）（地中海鲨鱼问题）

背景

建模与求解

模型分析

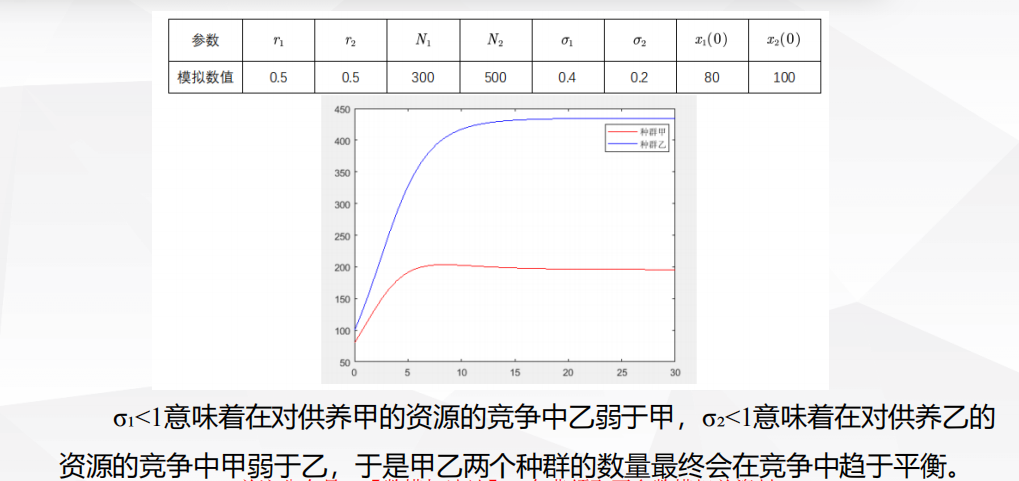
4.5 种群相互竞争模型

背景

建模与求解

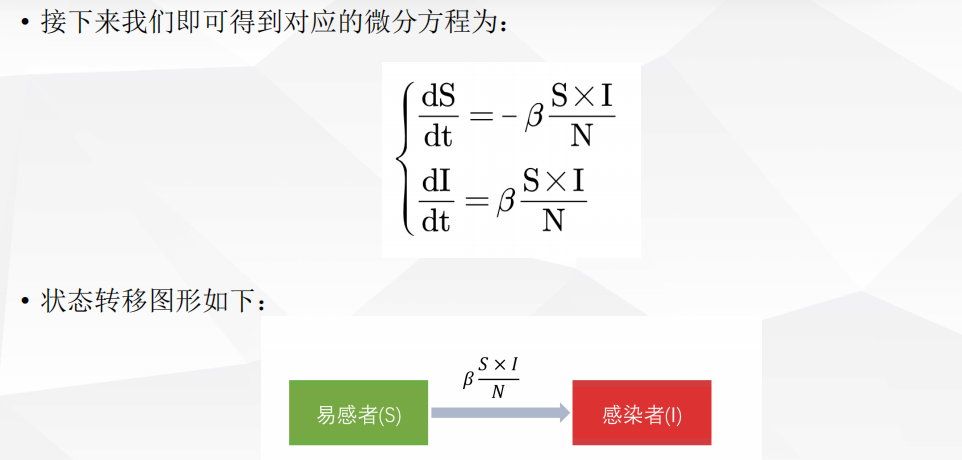
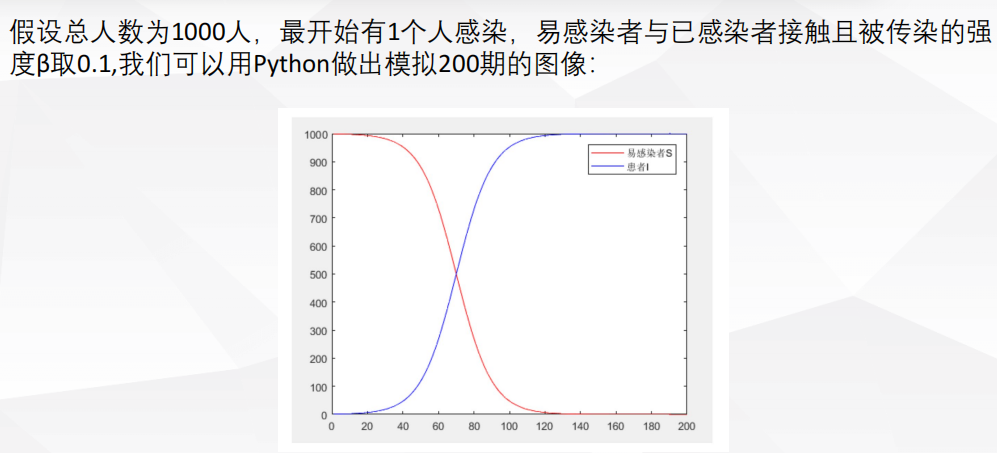
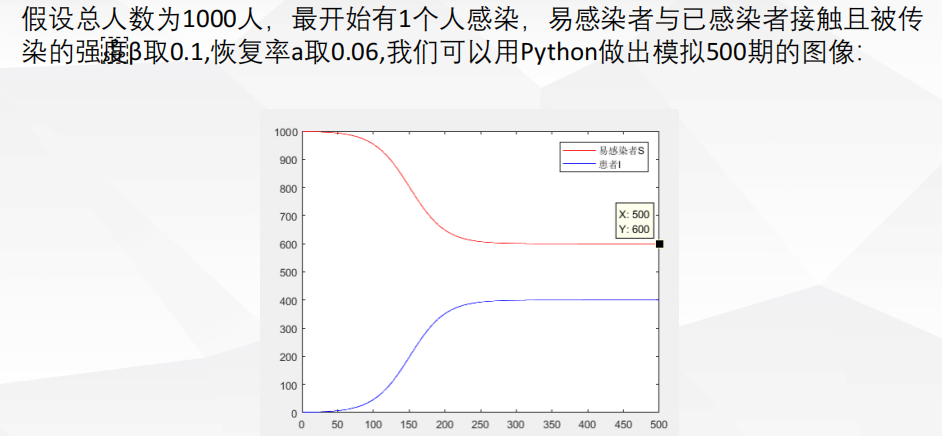
4.6 传染病模型

背景

建模求解

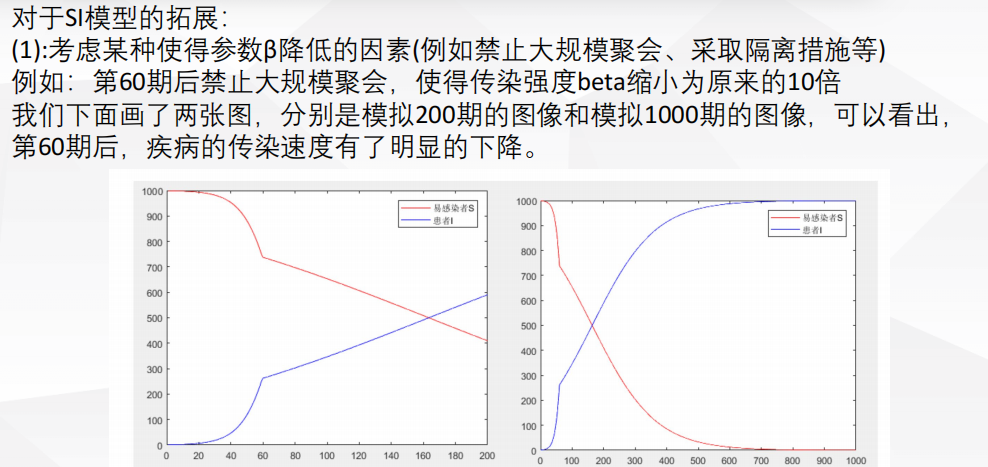
模型改进

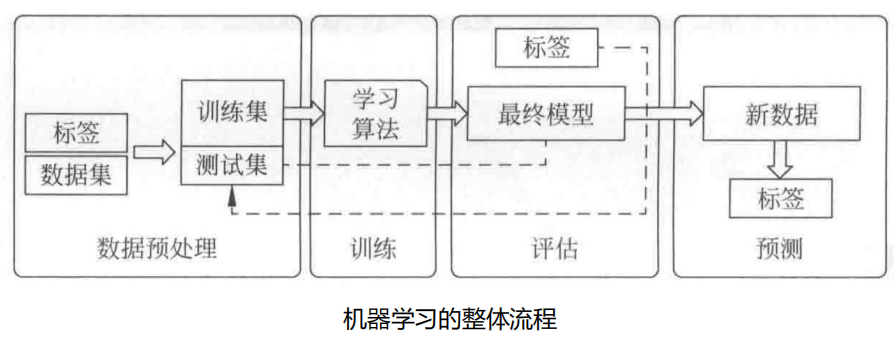
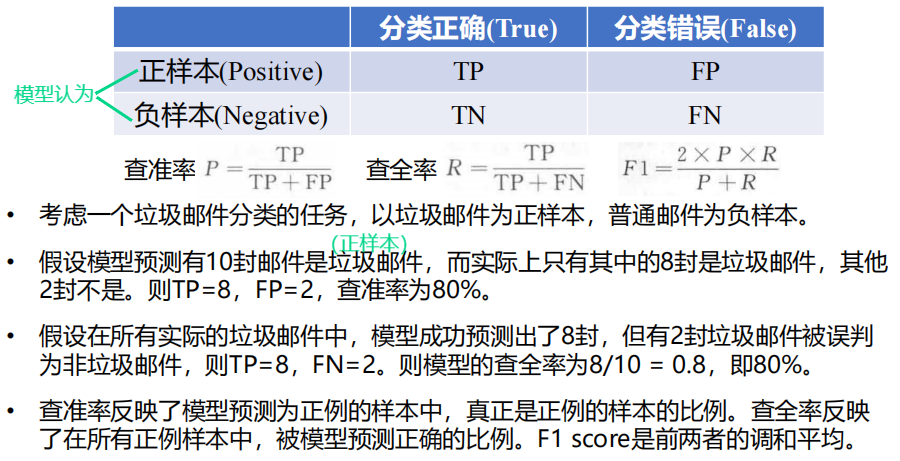
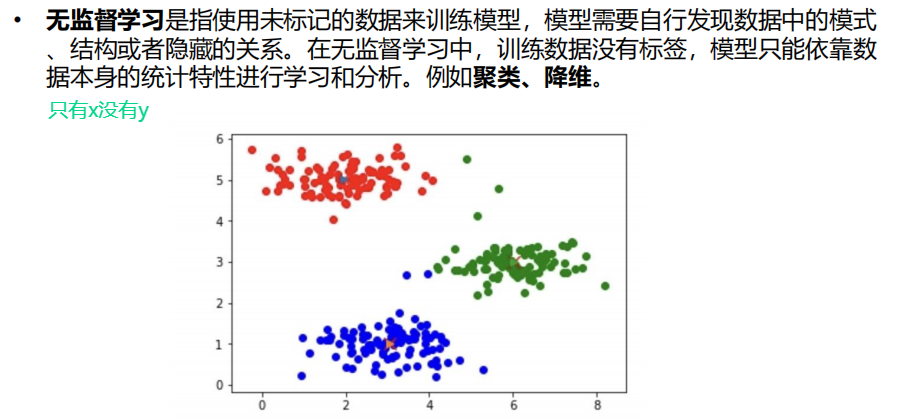
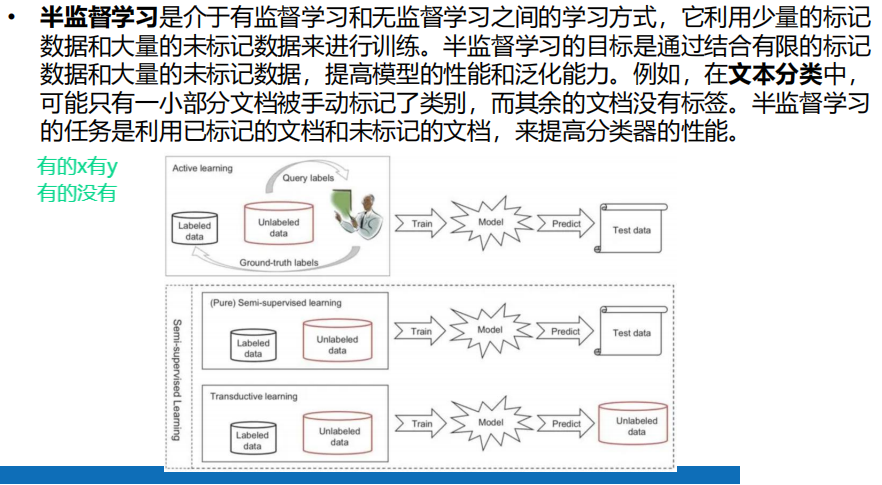
5 机器学习

5.1 机器学习概述

1 机器学习的任务

2 相关概念

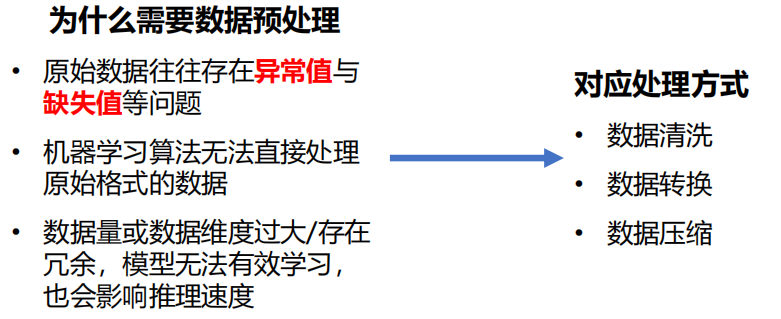
5.2 数据预处理

1 意义

2 数据清洗

基本任务

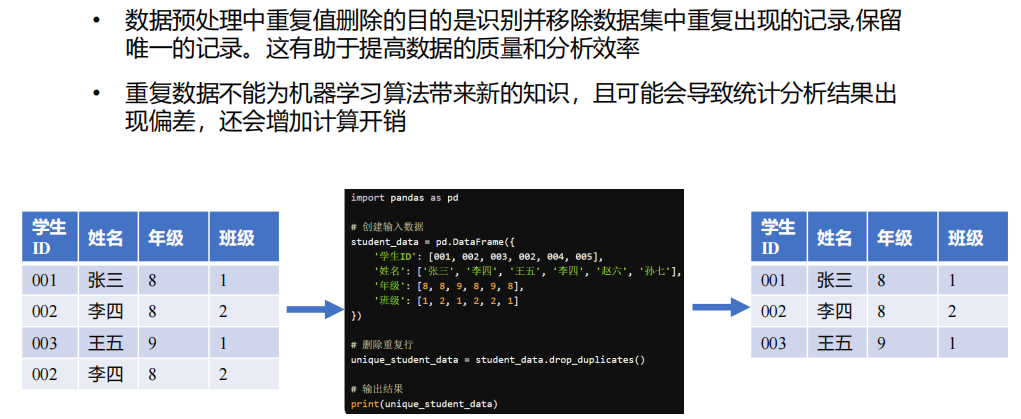
• 重复值删除
  
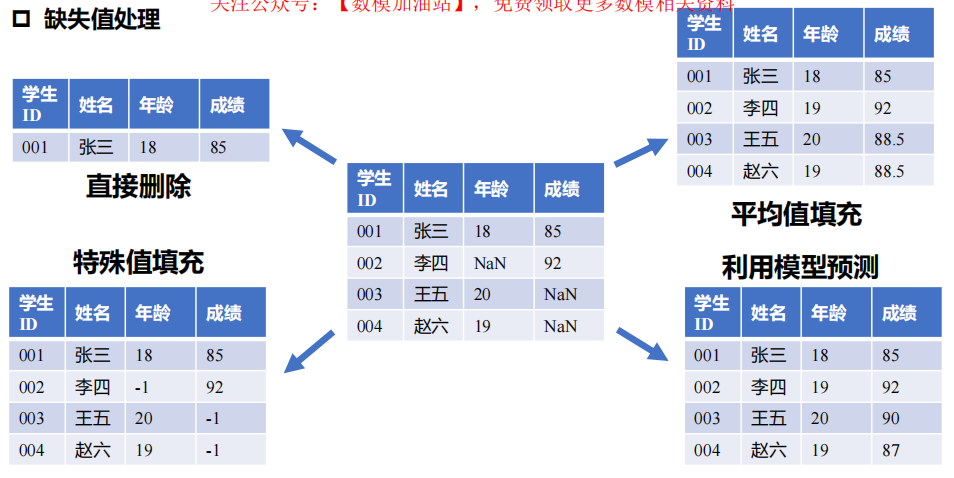
• 缺失值处理
  
  
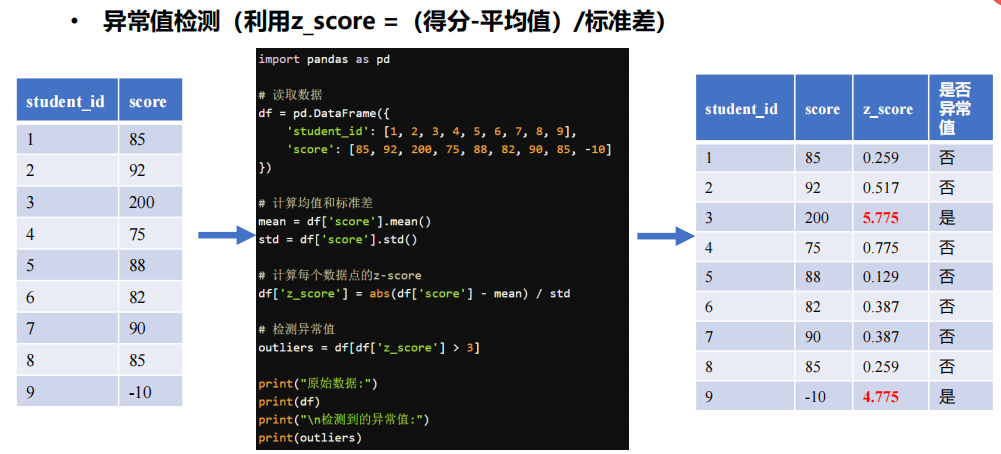
• 异常值处理
  
  

3 数据转换

4 数据压缩

5.3 简单分类算法

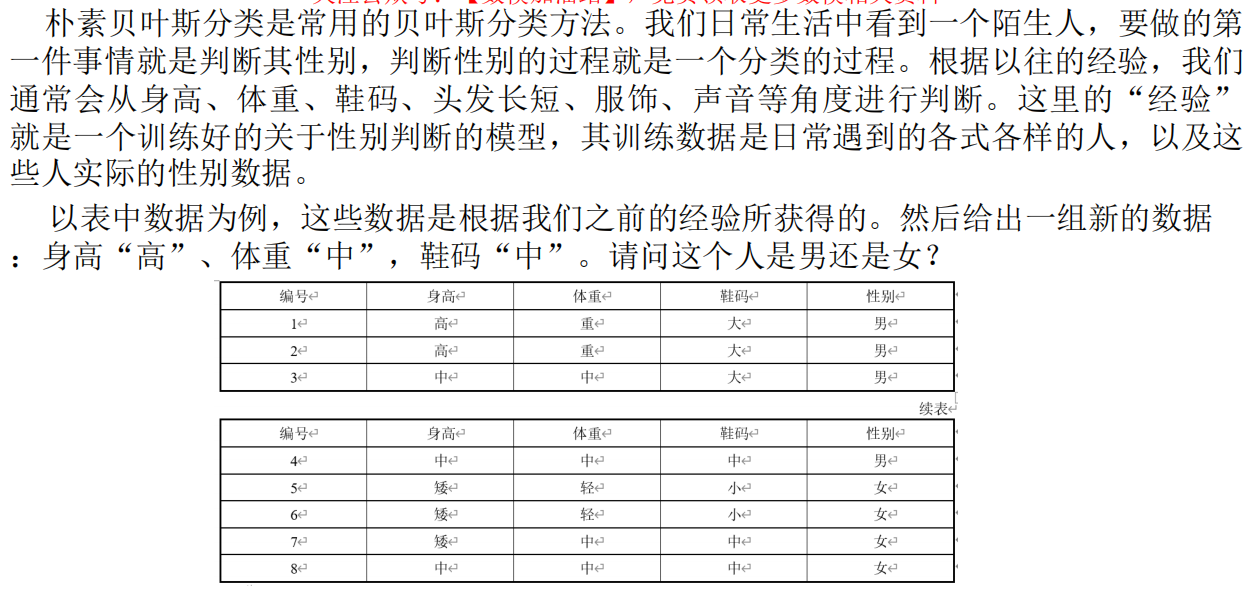
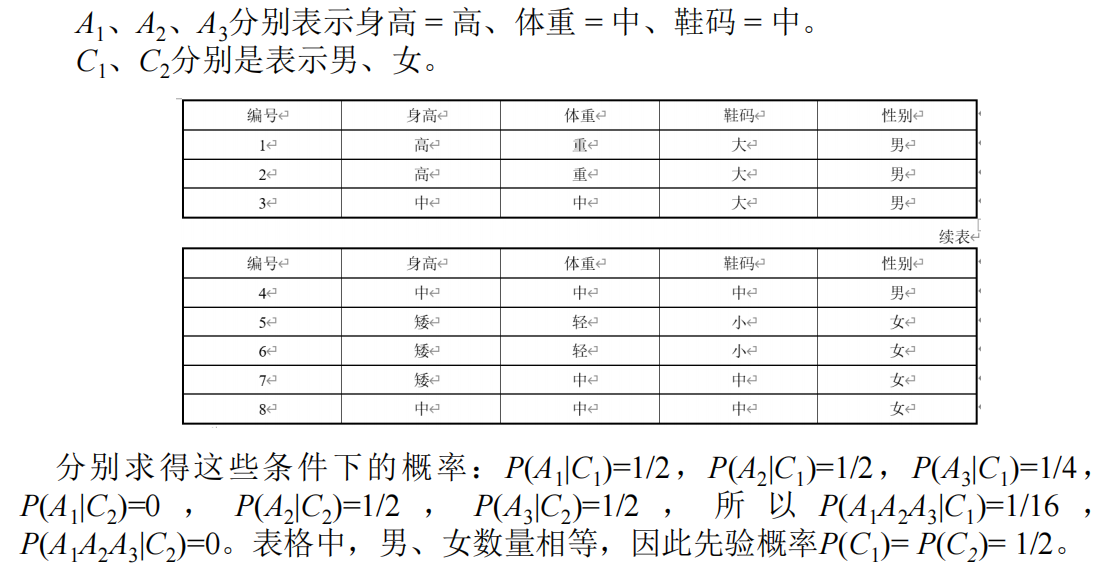
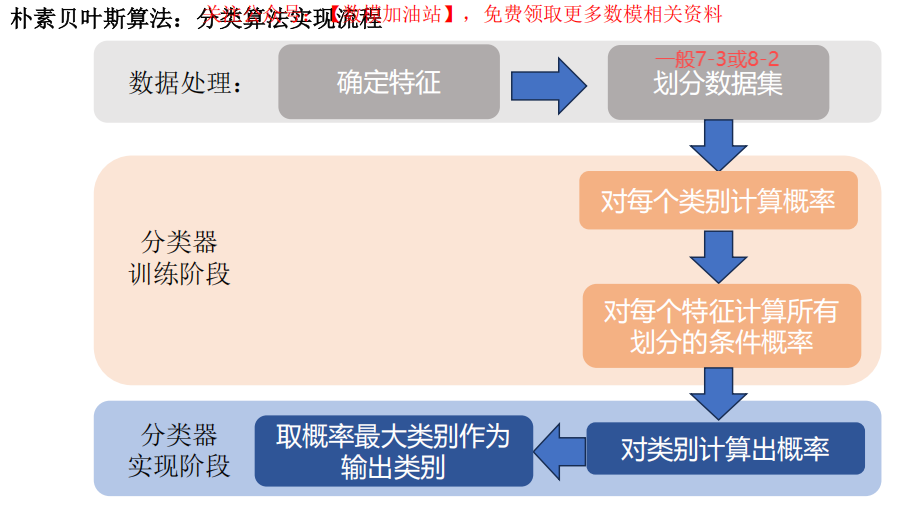
1 朴素贝叶斯分类算法（独立性假设！！！）

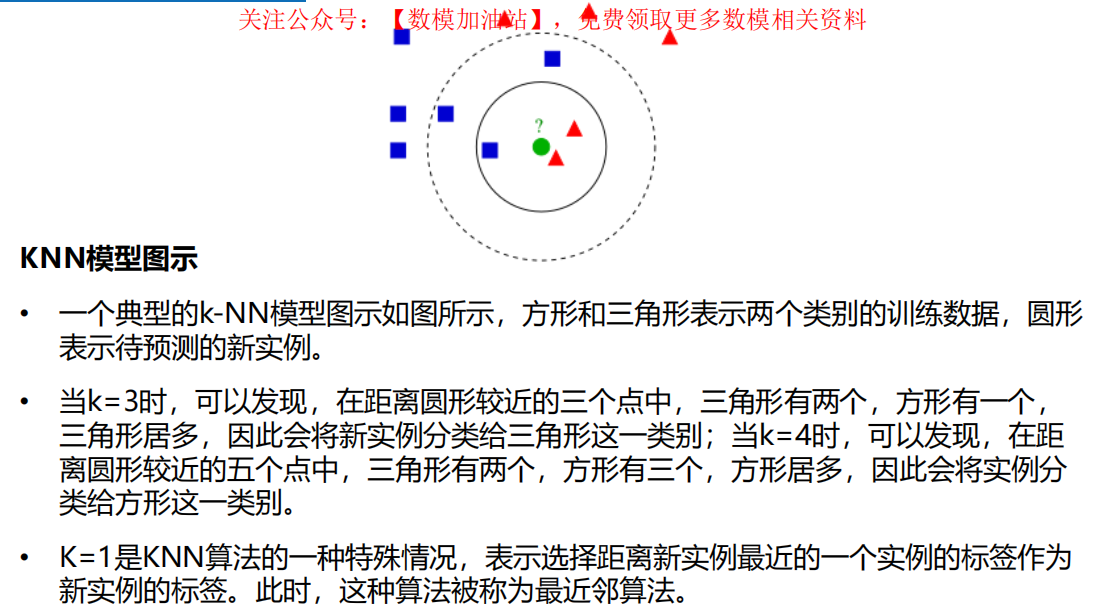
2 KNN分类算法

什么是KNN

直观理解KNN

KNN的要素

KNN的优缺点

3 项目实战：鸢尾花分类

5.4 贝叶斯心脏病预测

1 什么是贝叶斯

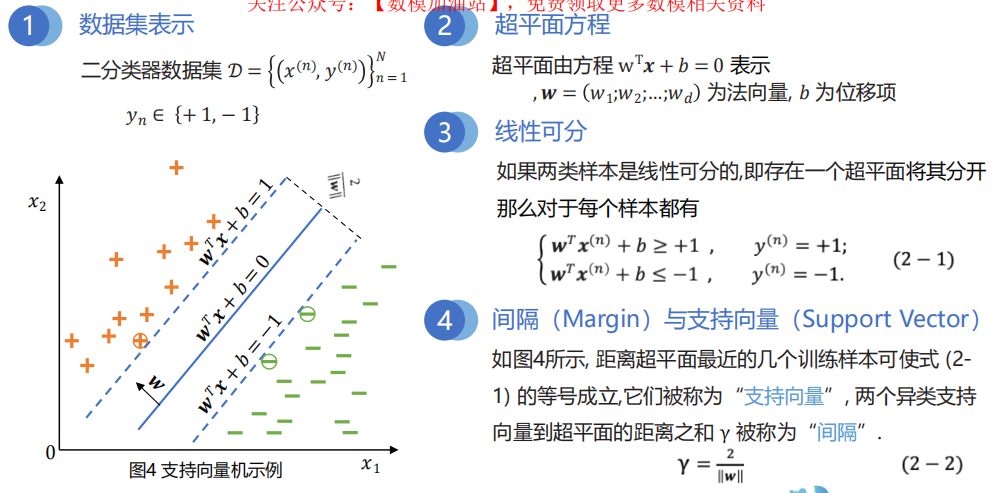
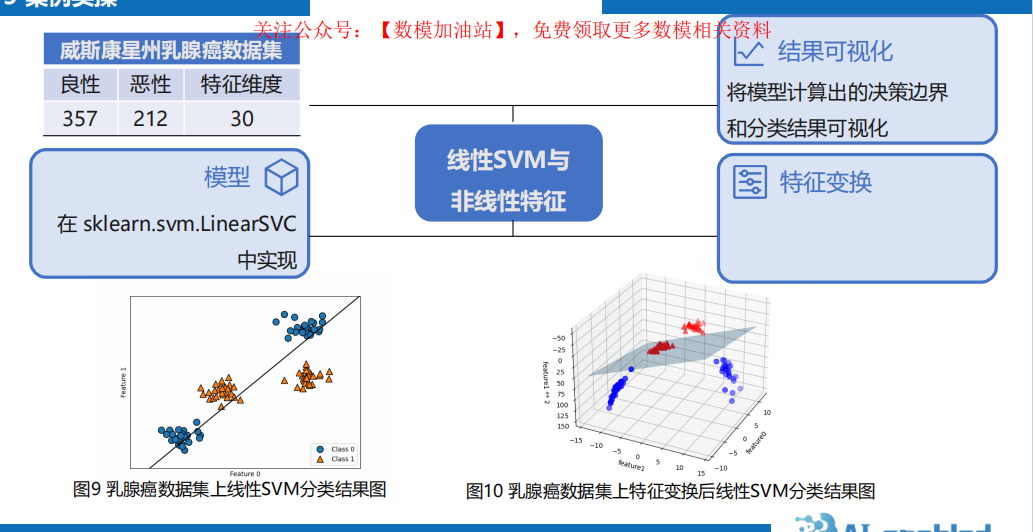
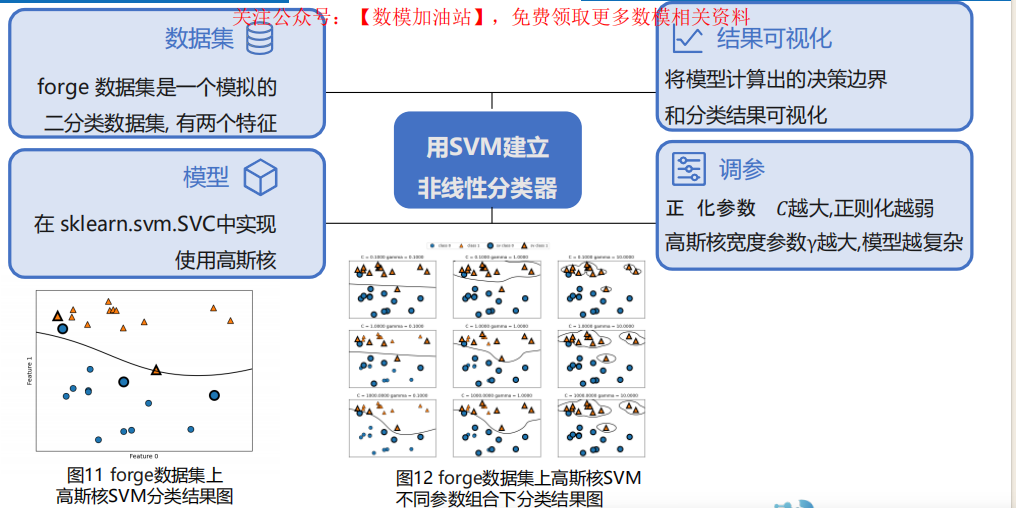
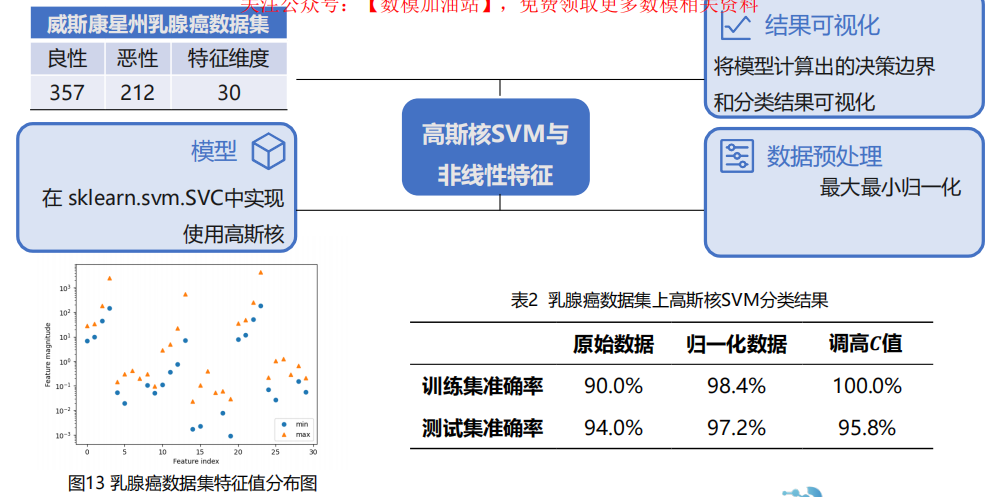
5.5 支持向量机 ( SVM support vector machine )

1 算法原理

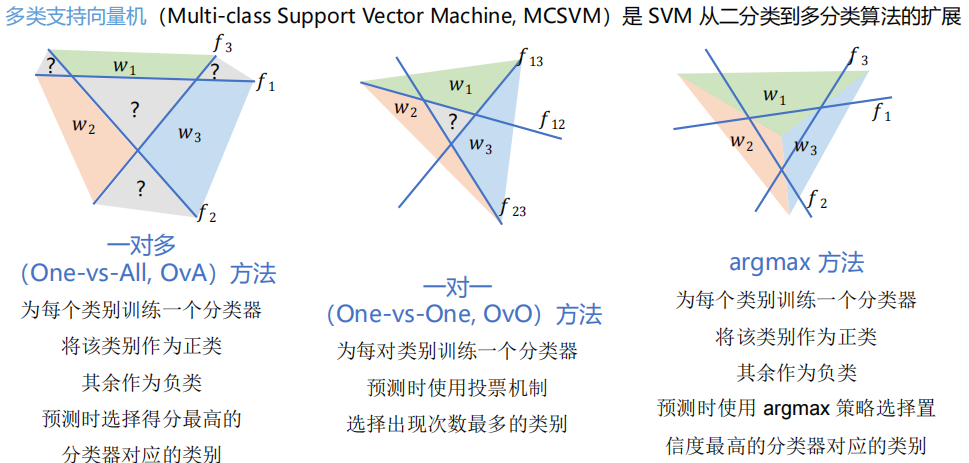
2 算法分析

3 算法拓展

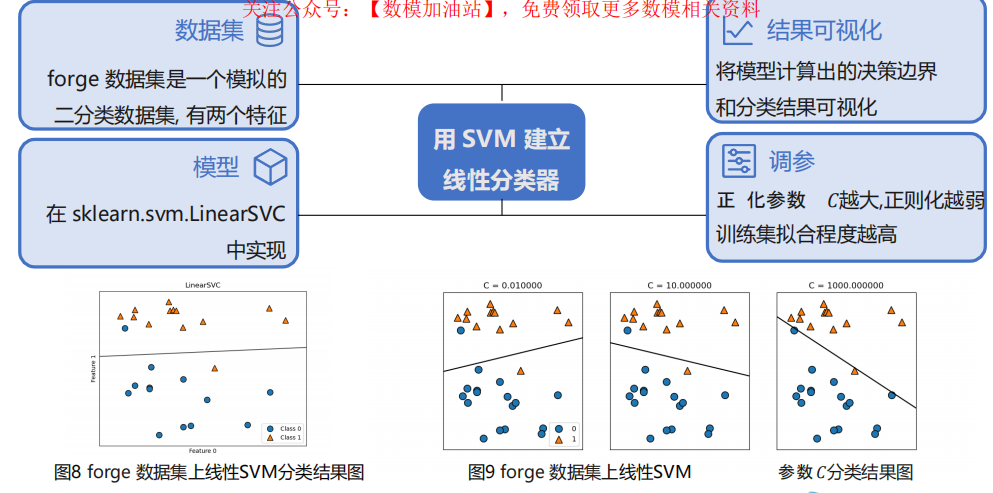
4 案例实操

6 智能优化算法

智能优化算法又称为现代启发式算法，是一种具有全局优化性能、通用性强、且适合于并行处理的算法。这种算法一般具有严密的理论依据，而不是单纯凭借专家经验，理论上可以在一定的时间内找到最优解或近似最优解。
特点：都是从任一解出发，按照某种机制，以一定的概率在整个求解空间中探索最优解。由于它们可以把搜索空间扩展到整个问题空间，因而具有全局优化性能。

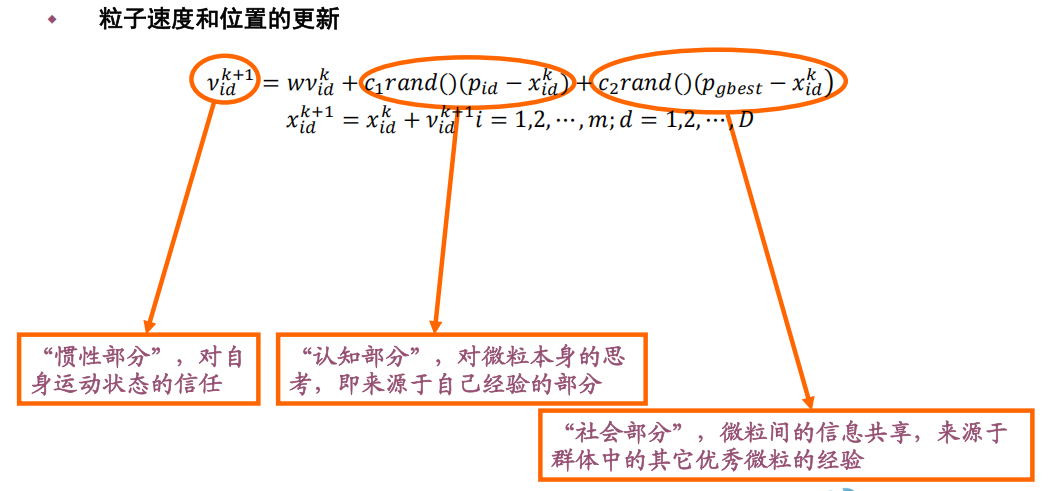
6.1 粒子群算法 ( PSO )

1 群智能

• 群智能（ Swarm Intelligence, SI ）
  人们把群居昆虫的集体行为称作“群智能”（“群体智能”、“群集智能”、“集群智能”等）
• 特点
  • 个体的行为很简单
  • 但当它们一起协同工作时，却能够突现出非常复杂（智能）的行为特征。

2 群智能算法

指无智能的主体通过合作表现出智能行为的特性，在没有集中控制且不提供全局模型的前提下，为寻找复杂的分布式问题求解方案提供了基础。

优点

• 灵活性：群体可以适应随时变化的环境；
• 稳健性：即使个体失败，整个群体仍能完成任务；
• 自我组织：活动既不受中央控制，也不受局部监管。

典型算法

• 粒子群算法（鸟群捕食）
• 蚁群算法（蚂蚁觅食）

3 基本原理

背景

原理描述

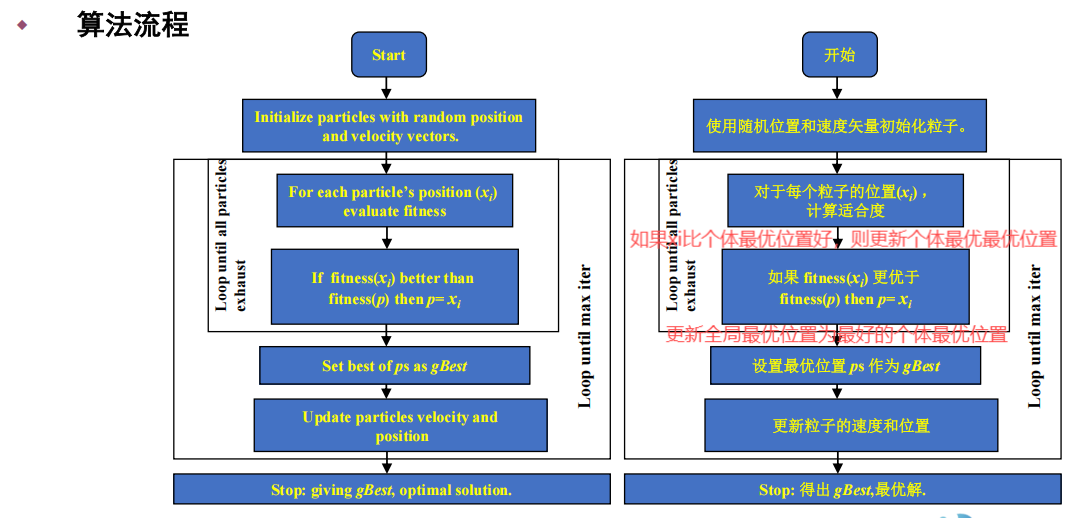
• 初始化为一群随机粒子，通过迭代找到最优。
• 每次迭代中，粒子通过跟踪“个体极值（pbest）”和“全局极值(gbest)”来 更新自己的位置。

算法

算法流程

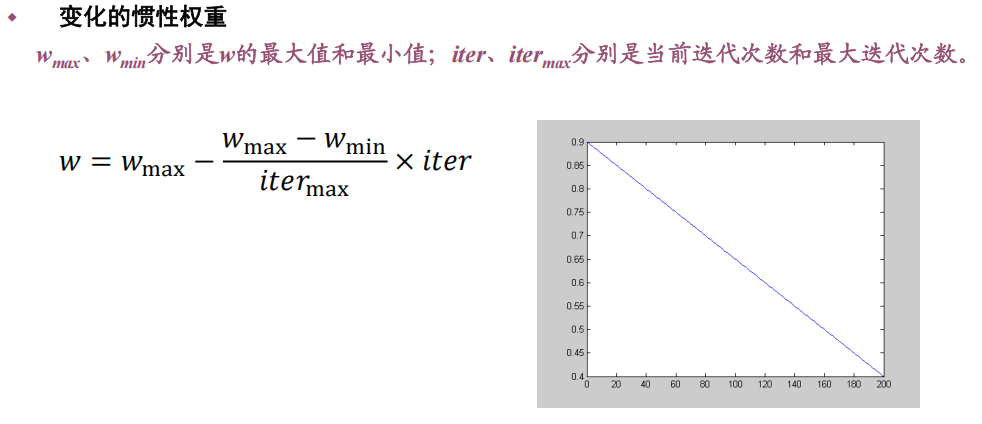
4 参数分析

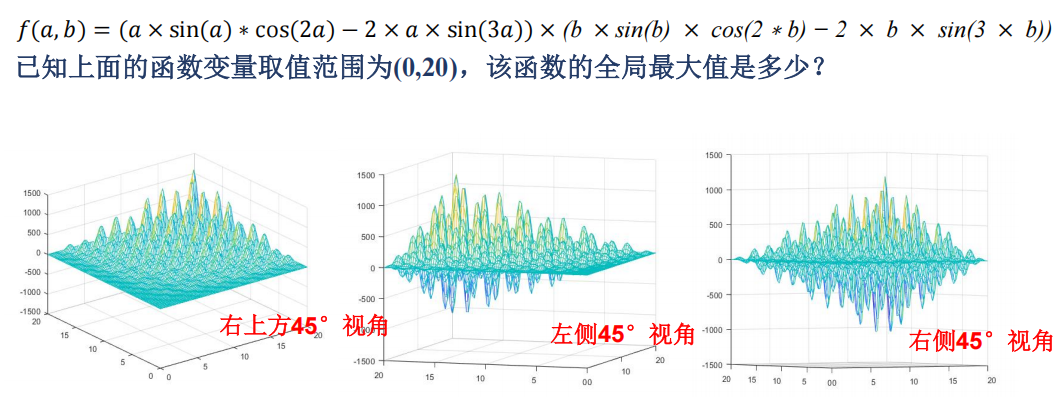
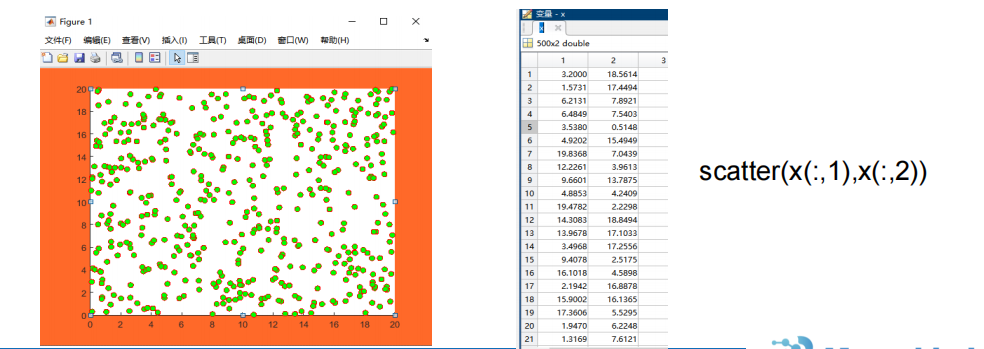
pro版

5 算法实现(有代码)

6 拓展：旅行商问题

7 群智能优化的特点和不足

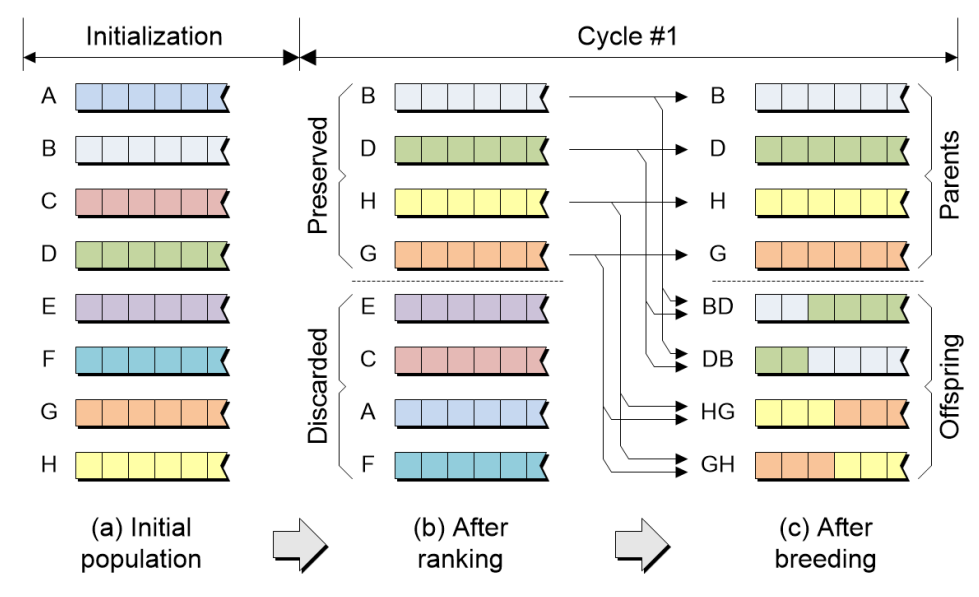
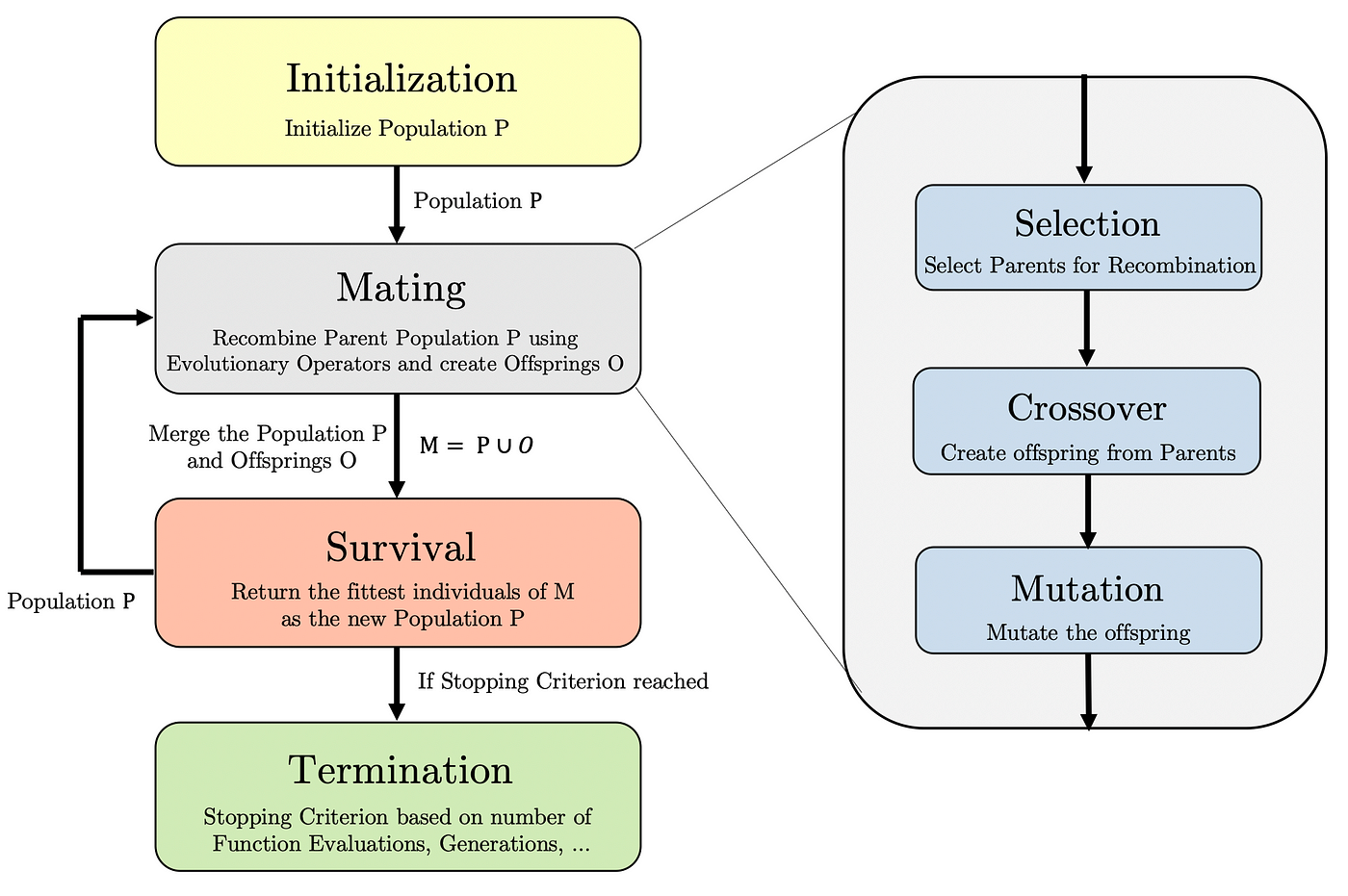
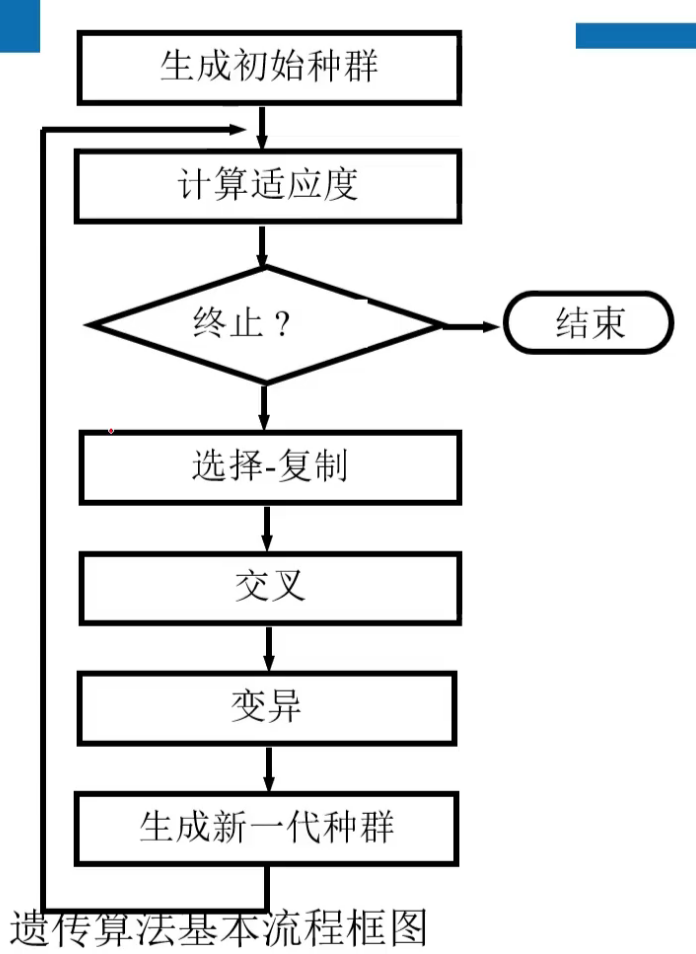
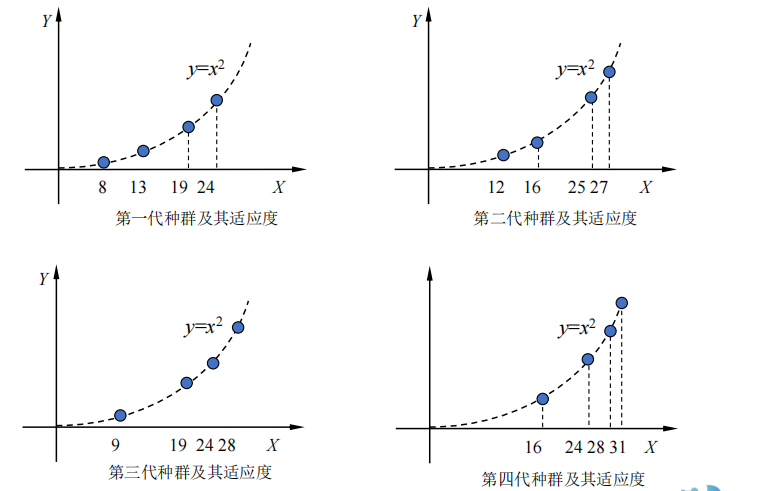
6.2 遗传算法

1 算法原理

• 染色体与基因
  
• 遗传操作
  
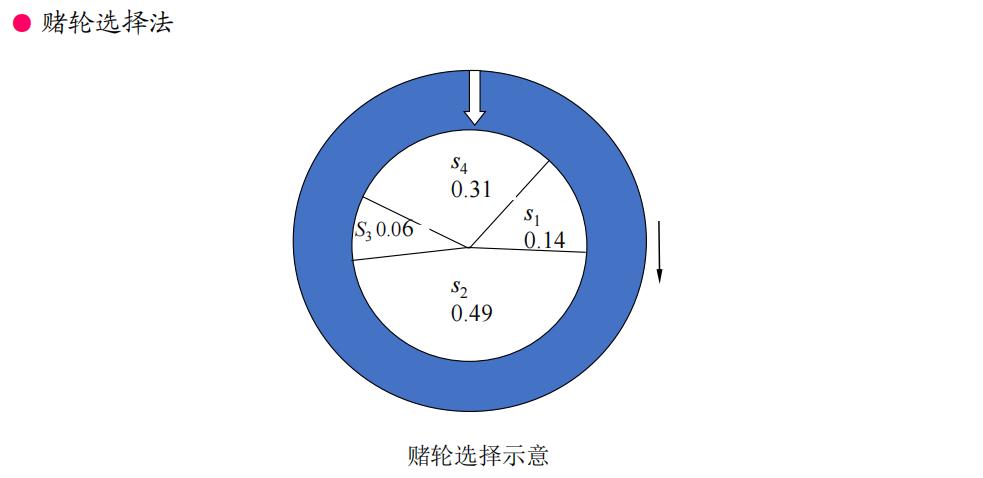
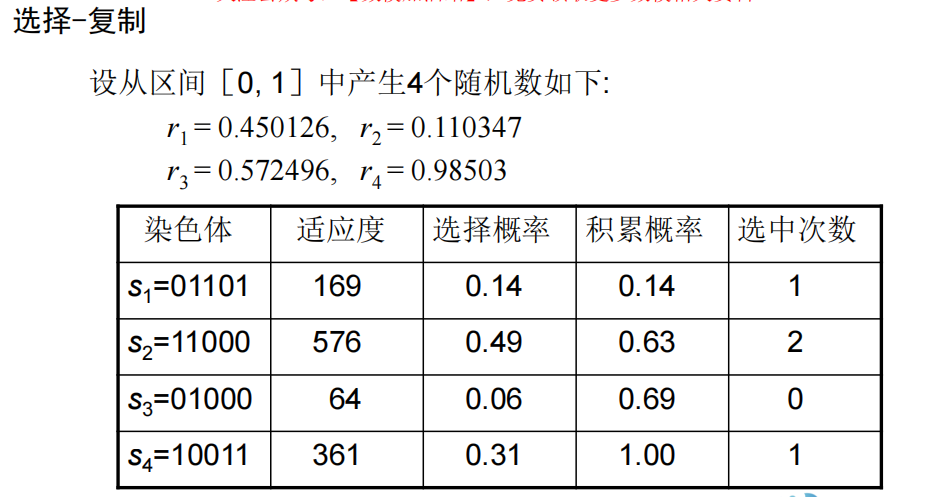
  • 选择-复制
    
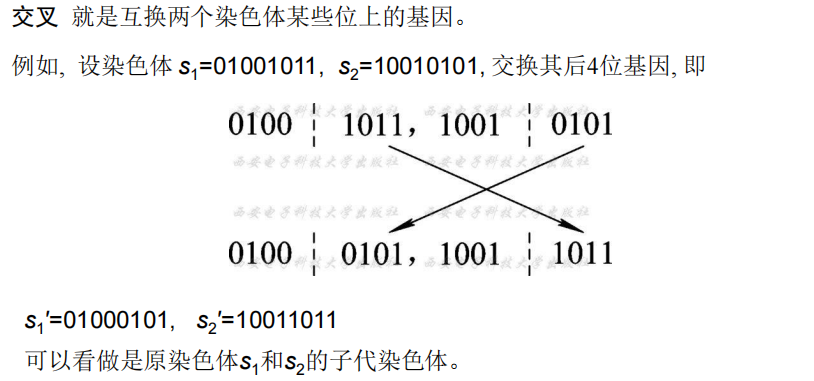
  • 交叉
    
  • 变异
    

算法流程

2 算法分析

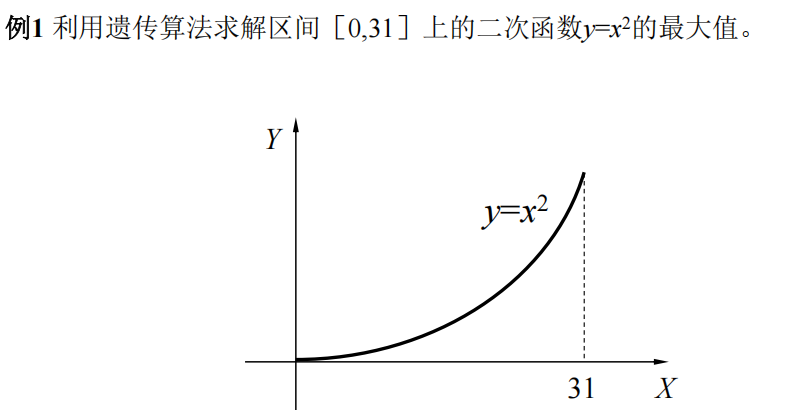
3 算法实现

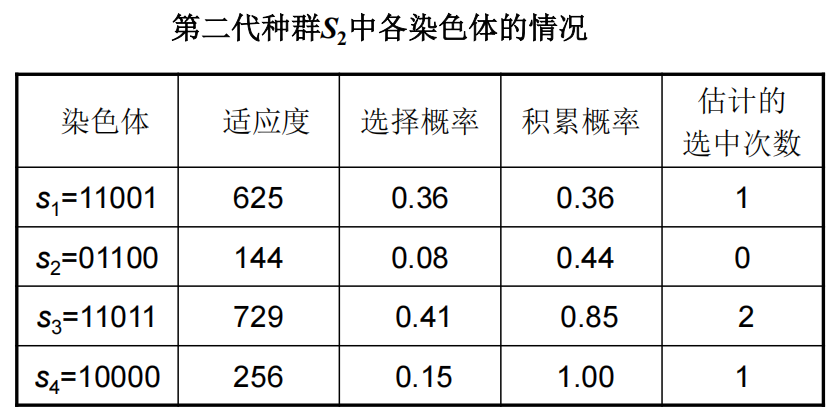
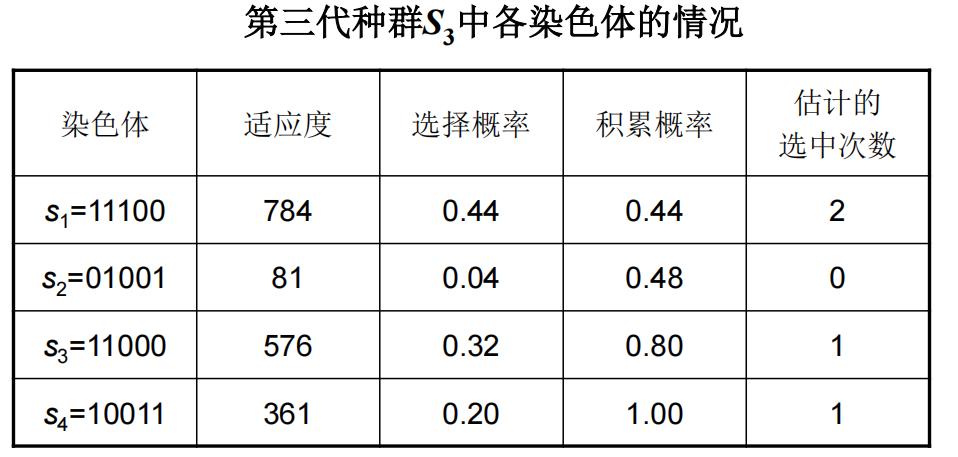
例1

总结

遗传算法的主要特点

• 遗传算法一般是直接在解空间搜索, 而不像图搜索那样一般是在问题空间搜索, 最后才找到解。
• 遗传算法的搜索随机地始于搜索空间的一个点集, 而不像图搜索那样固定地始于搜索空间的初始节点或终止节点, 所以遗传算法是一种随机搜索算法。
• 遗传算法总是在寻找优解, 而不像图搜索那样并非总是要求优解, 而一般是设法尽快找到解, 所以遗传算法又是一种优化搜索算法
• 遗传算法的搜索过程是从空间的一个点集(种群)到另一个点集(种群) 的搜索,而不像图搜索那样一般是从空间的一个点到另一个点地搜索。 因而它实际是一种并行搜索, 适合大规模并行计算,而且这种种群到种群的搜索有能力跳出局部最优解。
• 遗传算法的适应性强, 除需知适应度函数外, 几乎不需要其他的先验知识。
• 遗传算法长于全局搜索, 它不受搜索空间的限制性假设的约束,不要求连续性, 能以很大的概率从离散的、多极值的、 含有噪声的高维问题中找到全局最优解。

遗传算法的应用

• 遗传算法在人工智能的众多领域便得到了广泛应用。例如，机器学习、聚类、控制（如煤气管道控制）、规划（如生产任务规划）、设计（如通信网络设计、布局设计）、调度（如作业车间调度、机器调度、运输问题）、配置（机器配置、分配问题）、组合优化（如TSP、背包问题）、函数的最大值以及图像处理和信号处理等等。
• 另一方面，人们又将遗传算法与其他智能算法和技术相结合，使其问题求解能力得到进一步扩展和提高。例如，将遗传算法与模糊技术、神经网络相结合，已取得了不少成果。

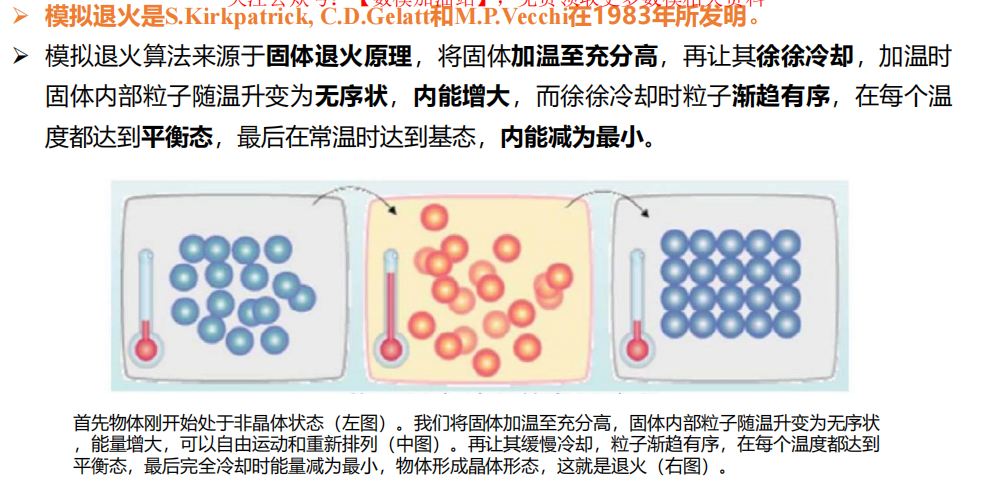
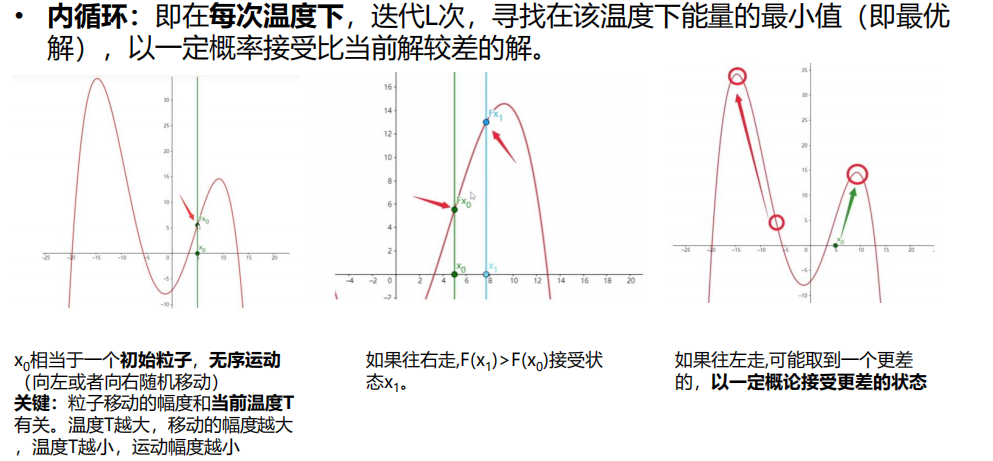
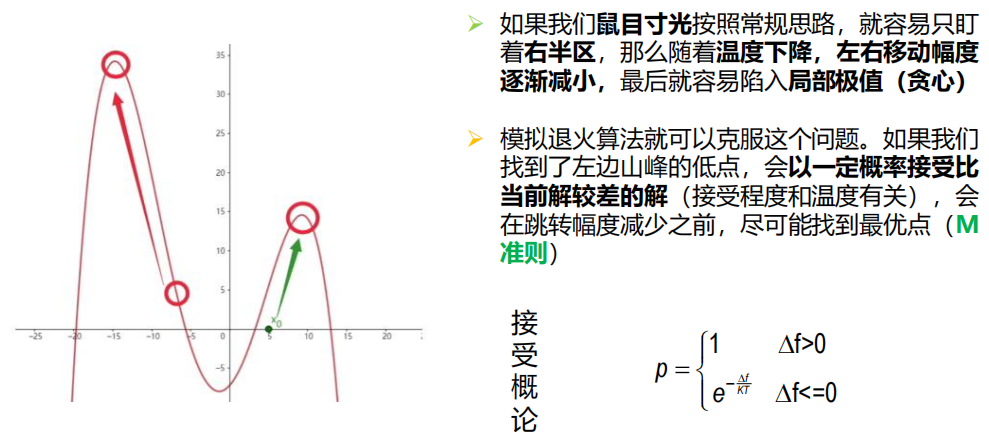
6.3 模拟退火算法

1 算法背景

2 算法原理

原理

3 算法流程

4 算法特点

5 算法拓展

6.4 天牛须搜索

1 算法背景

2 算法原理

3 算法分析

4 算法特点

• 优点
  • 运算量非常小，收敛非常快
  • 具有全局寻优能力
  • 代码非常简洁，容易实现
• 缺点
  • 有可能陷入局部最小值
  • 步长的选取需要根据实际情况确定
  • 迭代次数增加导致寻优步长过小

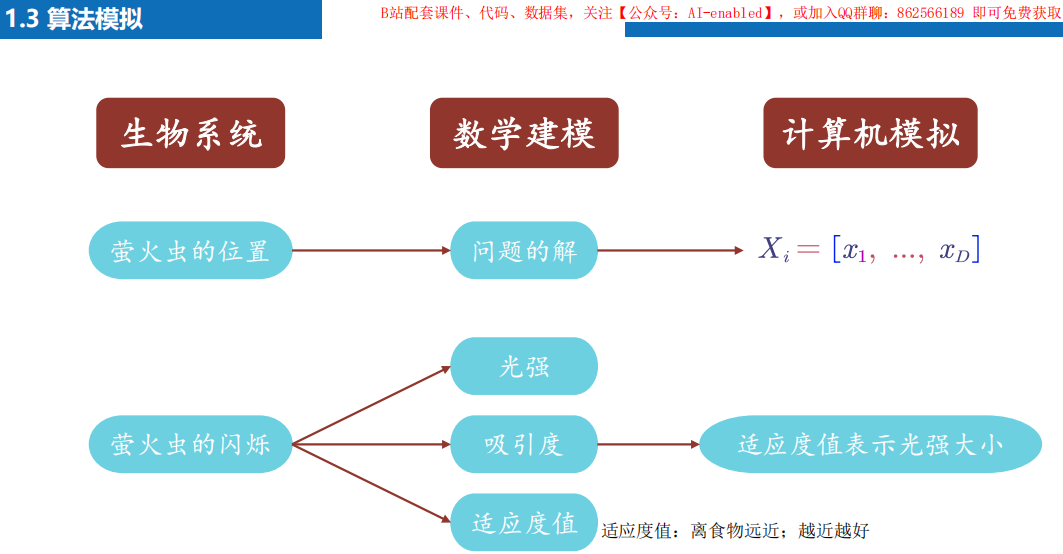
6.5 萤火虫算法

1 算法背景

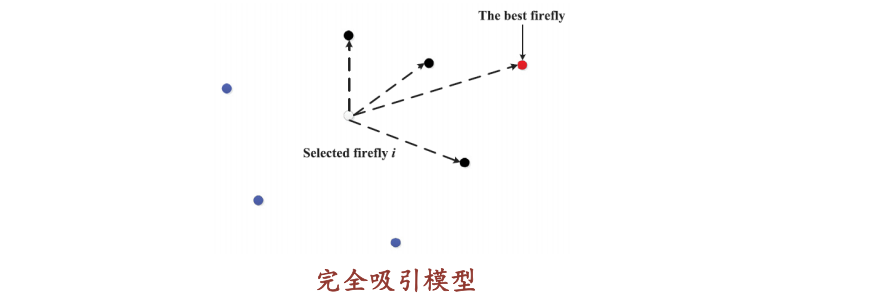
2 算法原理

算法原理

算法步骤

伪代码

3 算法改进

APFA 参数自适应策略

CFA 混沌映射策略

• 高斯映射

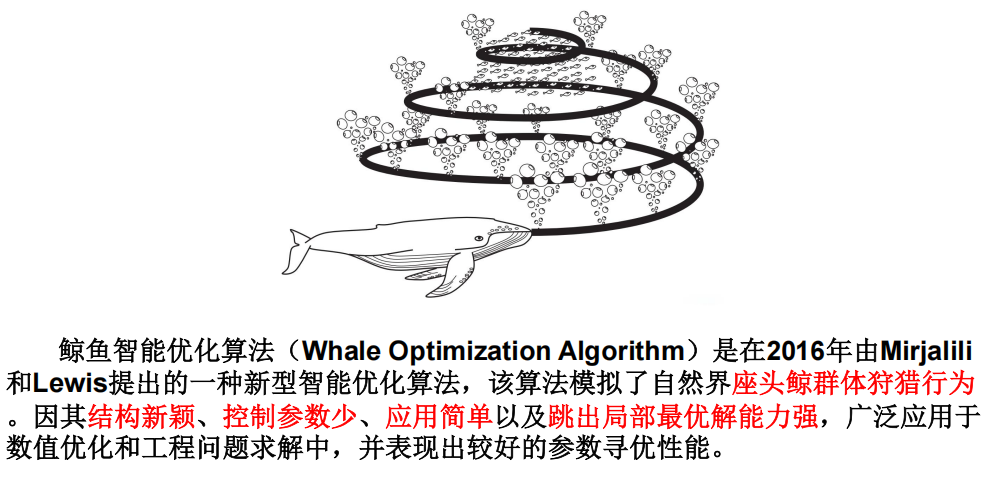
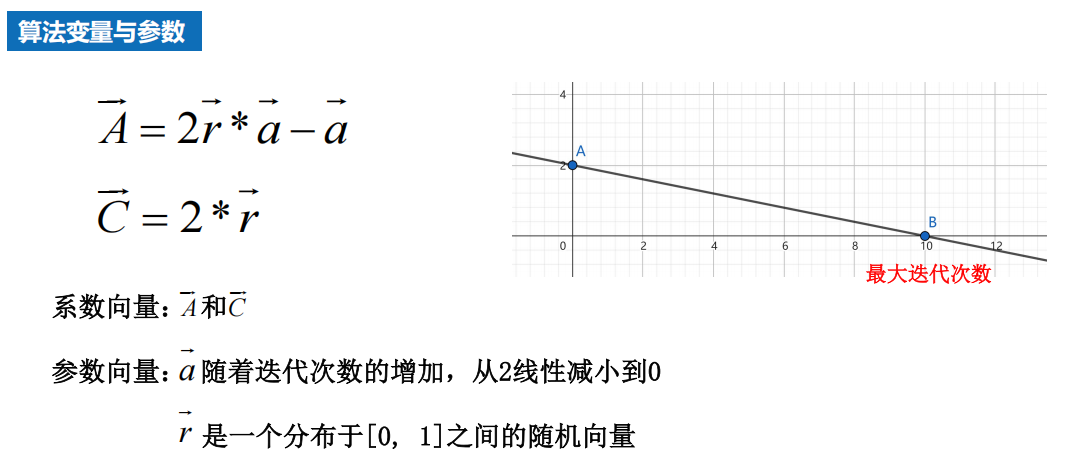
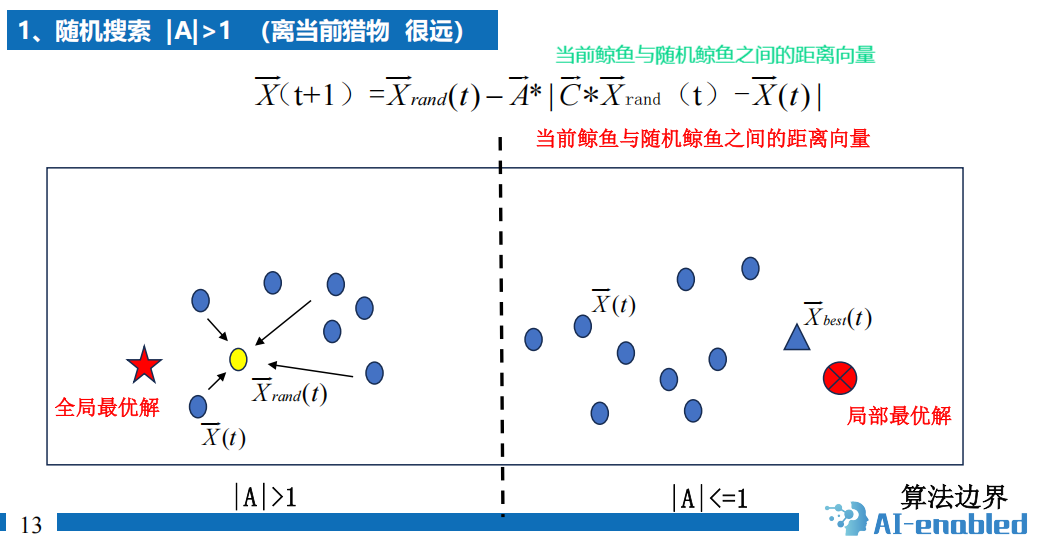
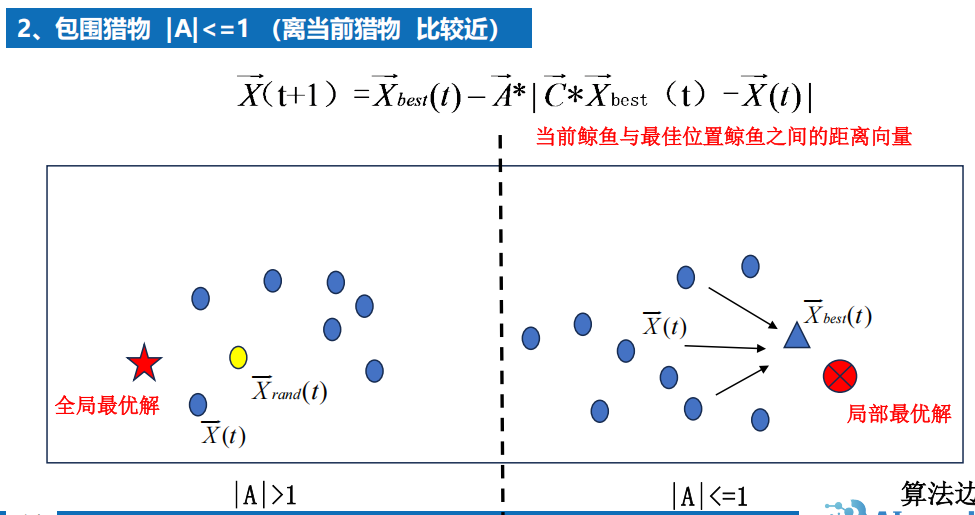
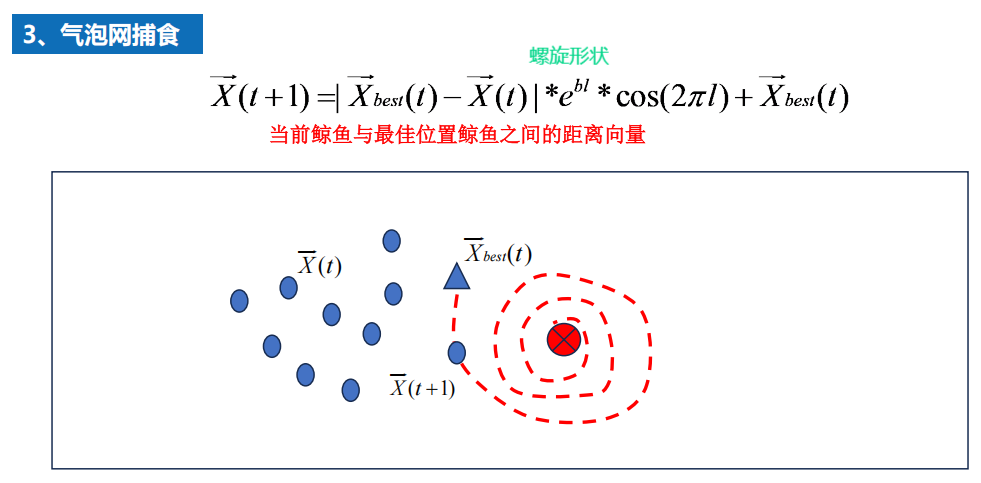
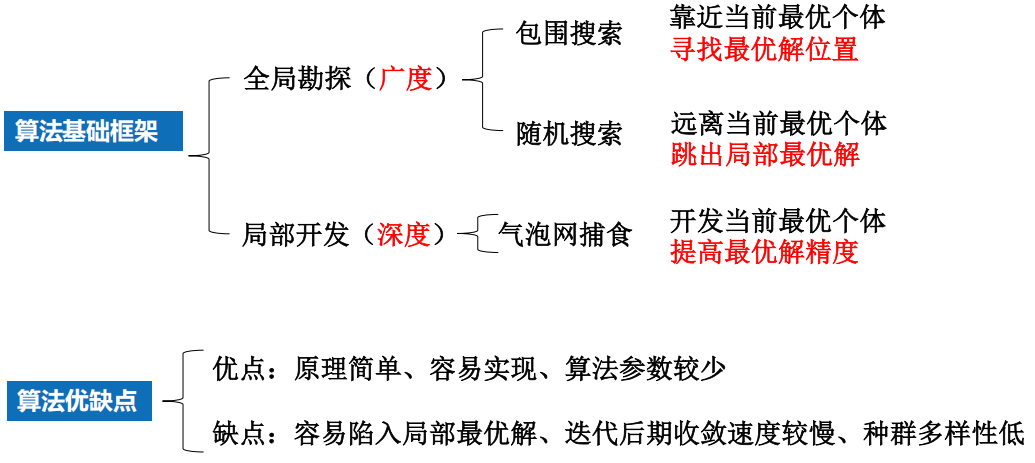
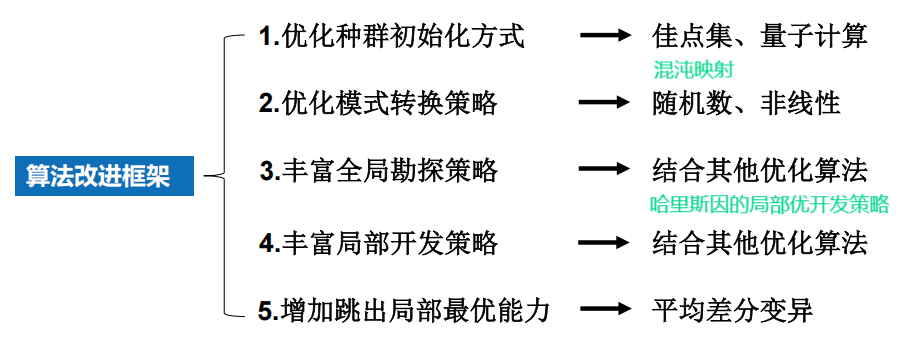
6.6 鲸鱼优化算法 效果不好？？？

1 背景

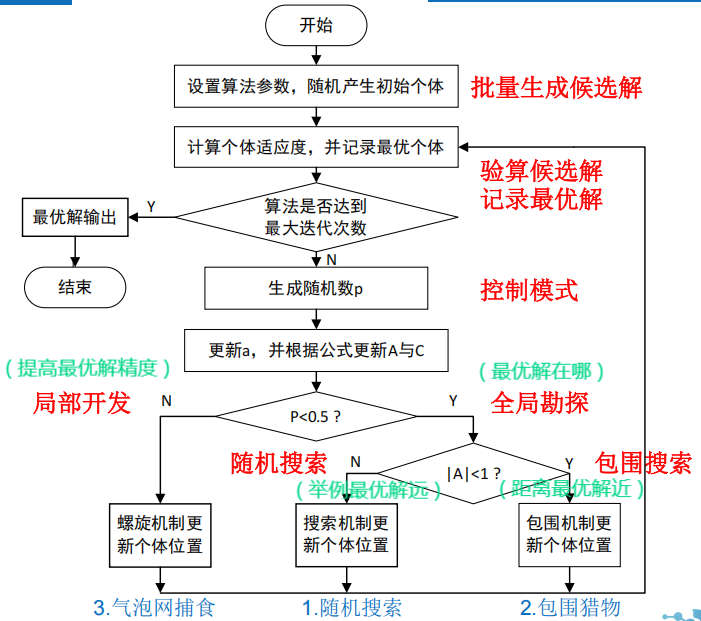
2 算法

流程图

原理

3 算法分析

4 算法拓展