-
关联、相邻、邻接
- 点和点:邻接
- 点和边:关联
- 边和边:相邻
-
导出子图:(点不一定全,边也不一定全,但只要两边的点都有就一定有边)设
的 端 点 都 在 中 -
生成子图:(只要求点是全的,边不一定全)设
有向图 通路 回路 连通
-
简单通路:有向图+无重复边
-
基本通路:有向图+无重复点
-
简单回路:有向图+一圈+无重复边
-
基本回路:有向图+一圈+除了始点终点无重复点
-
半通路(有边)、通路(有同向边)
-
完备通路:称通过有向图中所有顶点的通路为完备通路。
-
完备回路:称通过有向图中所有顶点的回路为完备回路。
-
完备半通路:称通过有向图中所有顶点的半通路为完备半通路。
-
u连接到v、u可达v(从
-
在
-
强连通的、3度连通的:(任意两点互相可达)
-
单向连通的、2度连通的:(任意两点至少一个方向可达)
-
弱连通的、1度连通的:(任意两点互相连接)
-
不连通的、0度连通的:(不弱连通)
-
有向图
-
有向图
-
有向图
无向图 链 连通
- 简单链:(各边不同)
- 基本链:(各点不同)
- 闭合链:(第一个点和最后一个点相同)
- 圈:(第一个点和最后一个点相同且各边不同)
邻接矩阵、可达性矩阵、关联矩阵
-
设
-
设
-
关联矩阵
有 向 图 若 是 弧 的 始 点 若 是 弧 的 终 点 若 不 是 弧 的 端 点 无 向 图 与 的 关 联 次 数
树
-
树的等价定义
设
-
有向树:将一个树的边加上任意的方向,就得到有向树。任何有向树都是弱连通的无回路有向图,但是弱连通的无回路有向图未必是有向树(如下图)。
-
树根、根数:若有向树 T 有一个顶点的引入次数为0,其余顶点的引入次数都为 1,则称 T 为根树。称根树中引入次数为 0 的顶点为树根。
-
树叶、分支顶点、级:从树根到一个顶点的通路的长度称为该顶点的级。
作为根树,以上两树是一样的,作为有序树,它们是不同的 -
每个顶点的引出次数都等于 m 或 0 的根树称为完全 m 元树。
-
若无向图 G 的生成子图 T 是树,则称 T 为 G 的生成树。
-
定理12.7:无向图 G 有生成树当且仅当它是连通的。
-
基本圈(一个弦+一堆树枝)、基本圈组(基本圈组成的集合):(n, m) 无向图 G 有 m-n+1 个基本圈
-
基本割集(一个树枝+一堆弦)、基本割集组(基本割集组成的集合):(n, m) 无向图 G 有 n-1 个基本割集
-
任何圈和任何割集都有偶数条(包含零条)公共边。
-
给定图
-
给定图
欧拉图和哈密顿图
-
欧拉圈、欧拉图、欧拉链
-
连通无向图
-
在连通无向图
-
欧拉回路、欧拉图、欧拉通路
-
强连通有向图
-
单向连通有向图
-
哈密顿圈、哈密顿图、哈密顿链
-
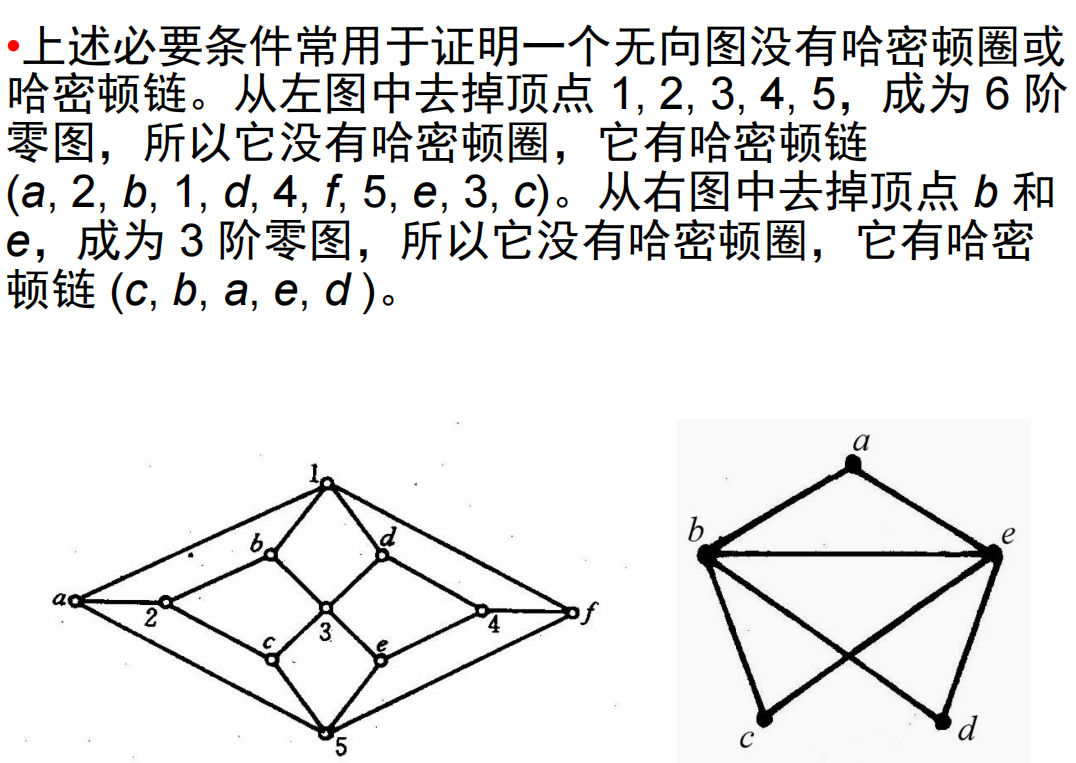
哈密顿图的必要条件(只能判断不是哈密顿图):若无向图
=
-
哈密顿链的必要条件(只能判断不是哈密顿链):若无向图
=
-
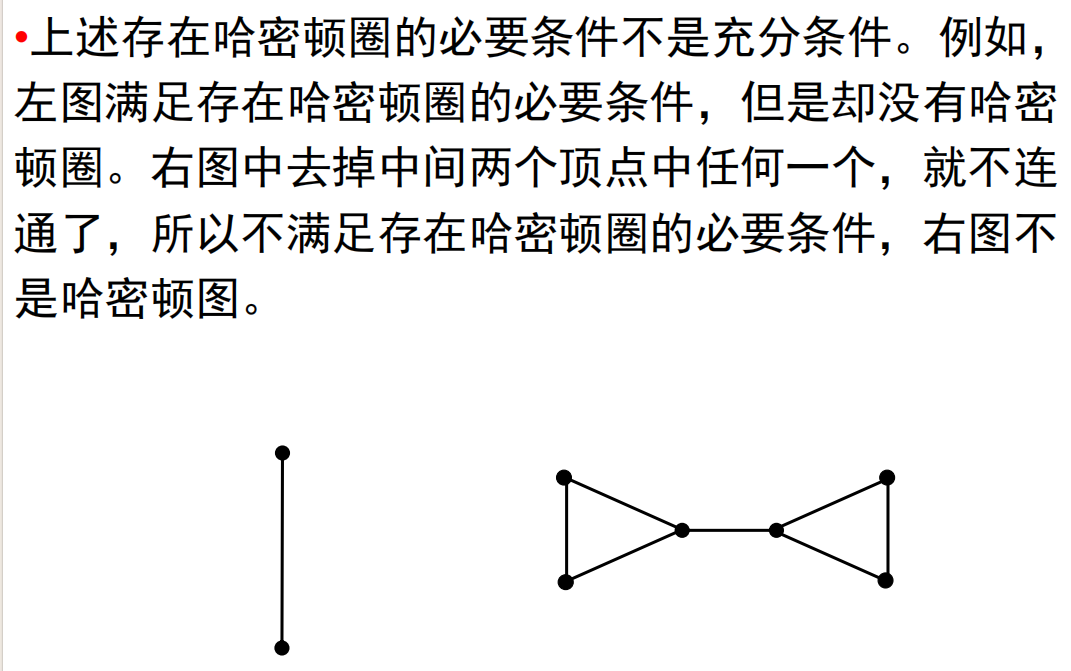
哈密顿图的充分条件:设
-
哈密顿链的充分条件:若
-
哈密顿回路、哈密顿图、哈密顿通路
-
在有向完全图中必存在哈密顿通路。
-
凡是强连通的有向完全图一定有哈密顿回路。
二分图
- 非平凡无向图
- 匹配:二分图左边的点和右边的点相连,每个点最多连一条线
- 最大匹配:在二分图
- 从 X 到 Y 的匹配
- 交错链、饱和顶点、非饱和顶点、可扩充链
- 定理14.2:二分图
- 从X到Y的匹配的充要条件:设
- 定理14.4 t条件 从X到Y的匹配的充分条件:设