9.1 有向图及无向图

• 有向图 (digraph)：，顶点弧， 是 中的一个二元关系。
• 无向图 ：，顶点边， 是 中元素无序偶组成的多重集合。把链接顶点 和 的边记做 。
• 有限图：若图的顶点集合是有穷集，则称为有限图。
• 带权图：每条弧或边制定了权的图。

9.2 图的基本结构

• 关联、相邻、邻接

  • 在有向图 中，若 ，则说 邻接到 ，或说笼统地说 和 邻接，并说 关联于 和 ， 是 的始点， 是 的终点， 和 是 的端点。称关联于同一顶点的不同弧为相邻的。
  • 在无向图 中，若 ，则说 和 邻接，并说 关联于 和 ， 和 是 的端点。称关联于同一顶点的不同边为相邻的。（显然无向图中无“邻接到”的概念。）
  • 点和点：邻接
  • 点和边：关联
  • 边和边：相邻

• 简单图

  • 两个端点相同的弧或边称为自环，即只与一个顶点关联的弧或边称为自环。
  • 在有向图中，始点和终点分别相同的两条弧称为平行弧。在无向图中，两个顶点之间的两条边称为平行边。
  • 有平行弧的有向图称为多重弧图，有平行边的无向图称为多重边图。多重弧图和多重边图统称为多重图。
  • 无自环和平行弧（或平行边）的图称为简单图。
  • 对于简单有向图 ， 是 上的反自反关系(因为不存在自环)，它的图形表示是 的关系图。

• 顶点的次数(degree)

  • 引出弧、引入弧（有向图）
    在有向图中，设 为一顶点，称以 为始点的弧为 的引出弧，以 为终点的弧为 的引入弧。
  • 引出次数、引入次数（有向图）
    • 在有向图中，对于任意顶点 ，称顶点 的引出弧的条数为 的引出次数(out-degree)，记为 ；称顶点 的引入弧的条数为 的引入次数(in-degree) ，记为 。
    • 设 是有向图，。始点在 中且终点不在 中的弧的条数称为 的引出次数，记为 。终点在 中且始点不在 中的弧的条数称为 的引入次数，记为 。
  • 次数（有向图、无向图）
    • 有向图： 的引出次数与引入次数之和称为 的次数，记为 ，即
    • 无向图：无向图中，与顶点 关联的边的数目称为 的次数，记为 。需要注意，因为无向图中与 关联的自环的两个端点都是 ，所以应将自环计为两条边。
  • n阶图、(n,m)图
    若图 有 个顶点，则称 为 阶图。有 条边或弧的 阶图称为 图，并用 , 或分别表示图的顶点个数、弧的条数或边的条数
  • 孤立点
    次数为 0 的顶点称为孤立点，显然，孤立点与图中任何顶点都不邻接。
  • 悬挂点
    次数为 1 的顶点称为悬挂点，显然悬挂的只与图中其他顶点中的一个顶点邻接
  • 悬挂边
    与悬挂点关联的边称为悬挂边。
  • 零图
    每个顶点都是孤立点的图称为零图。
  • 平凡图
    1 阶零图，即仅由一个孤立点构成的图称为平凡图

• 握手定理

  • 对于顶点集合为 的 有向图，
  • 对于顶点集合为 的 有向图，
  • 次数为奇数的顶点称为奇顶点，次数为偶数的顶点称为偶顶点。
  • 在任何图中，奇顶点的个数必为偶数。

• 正则图
  若无向图 的所有顶点的次数都是同一个数 ，即对于任何 均有 ＝＝常数，则称 为 次的正则图。

• （无向）完全图
  任何两个顶点之间都有一条边的简单无向图称为完全图，将 n 阶完全图记为 。 是 次正则图，它的边数为

• 有向完全图
  任意两顶点之间都恰有一条弧的简单有向图称为有向完全图，也称为竞赛图。在 阶有向完全图中，每个顶点的次数都是 ，边数为 。

• 图的同构

  • 无向图：设 和 是两个无向图。若存在双射 使得， 当且仅当 ，并且重数相同，则称 和 是同构的。
  • 有向图：设 和 是两个有向图。若存在双射 使得， 当且仅当 ，并且重数相同，则称 和 是同构的
  • 性质（必要但不充分）
    • 同样的顶点数。
    • 同样的边数。
    • 对于任意自然数 ，次数为 的顶点数一样多。
    • 有同样多的自环。

9.3 子图

• 子图/部分图：设 和 是两个图。若 且 ，则称 为 的子图/部分图，记为 。

• 真子图：若 且 ，则称 为 的真子图。

• 补图：设 和 是图 的两个子图。若 ，并且 与关联是中孤立点，则称 为 相对于 的补图。

  • 补图中点和边的关系：若 是 相对于 的补图，则：
    • 中的每条边只能在 或 中一个里面出现，而不能够在两个中都出现
    • 的某个顶点可能同时在 和 中都出现。

• 无向图

  • 导出子图：（点不一定全，边也不一定全，但只要两边的点都有就一定有边）设 是 的子图。若 的端点都在中，则称 为 的由 导出的子图，或简称 的导出子图。
  • 生成子图：（只要求点是全的，边不一定全）设 是 的子图。若 ，则称 为 的生成子图。
  • 去点运算：从图 中去掉顶点 及与其关联的边得到的子图记为 。
  • 去边运算：从图 中去掉边 得到的子图记为 。
  • 加法运算：设无向图 中顶点 和 不相邻，在 中增加边 得到的图记为 。显然 是 的子图。
  • 图的并集：如果 ＝，＝，定义 ＝ 是 ＝ 和 ＝， 的并，记为 ＝

• 有向图的导出子图：设 ＝ 是有向图 的子图，如果 的各条弧是由 的所有在 中拥有始点和终点的那些弧所组成，即 的始点和终点都在中，则称 为顶点集合 所导出的子图，或简称图 的导出子图。

9.4 连通性

9.4.1 有向图 通路 回路 连通

• 通路：在有向图 中，首尾相接的弧的序列 称为通路。

• 长度：（通路中有几个弧（可重复））在通路 ＝ 中，对于每个 ， 的终点是 的始点，并称通路中弧的数目 为该通路的长度，记为 。（显然重复出现的弧按照重复次数计入）

• 简单通路：（无重复边）若通路 中的弧 都不同，则称它为简单通路。

• 基本通路：（无重复点）若通路 中的顶点 都不同，则称它为基本通路。

• 基本通路必是简单通路，简单通路未必是基本通路。

• 回路：（一圈）若通路 的始点 和终点 相同，则称它为回路。

• 简单回路：（一圈+无重复边）若一个回路又是简单通路，则称它为简单回路。

• 基本回路：（一圈+无重复点）若回路 中的顶点 都不同，则称它为基本回路。

• 无回路图：（没圈）没有回路的有向图称为无回路图。

• 可到达：（从 到 有“正向”边）若存在从顶点 到顶点 的通路，则说 可以到达 。

  • 可达关系是顶点集 上的自反的、传递的关系。
    每个顶点 可达自己（从 到 有长度为0 的通路）。
    若有从 到 的通路 和从 到 的通路 ，则将它们首尾相接就得到从 到 的通路 , 。
  • 可达关系 不一定具有对称性和反对称性。

• 半通路：（从 到 有边（不管方向））在有向图 中，每条弧（除最后一条弧之外）都与随后那条弧相邻的弧的序列 称为半通路。
  通路是每条弧都是从前向后的半通路。也将半通路 记为顶点的序列 ，其中对每个 ， 或者 。

• u连接到v：若存在从顶点 到顶点 的半通路，则说 连接到 。

  • 如果 连接到 ，则 也连接到 。
  • 从 到 的半通路也是从 到 的半通路。连接关系 是顶点集 上的等价关系。

• 若从顶点 可以到达顶点 ，则存在从 到 的基本通路。

• 到 有通路，则必有基本通路，且最短通路必是基本通路；从而 到 无基本通路，则必无通路

• 从u到v的距离

  • 可能存在若干条从 到 的通路，他们有相同的最短长度
  • 距离不一定是对称的，可能会有
  • 当且仅当
    从到的最短通路的长度从可到达

• （三角不等式）

• 在 阶有向图中，任何基本通路的长度都不超过 ，任何基本回路的长度都不超过 。

• 强联通的：（任意两点互相可达）在有向图 中，如果任取一对顶点 和 ， 可以到达 且 可以到达 ，则称 为强连通的。

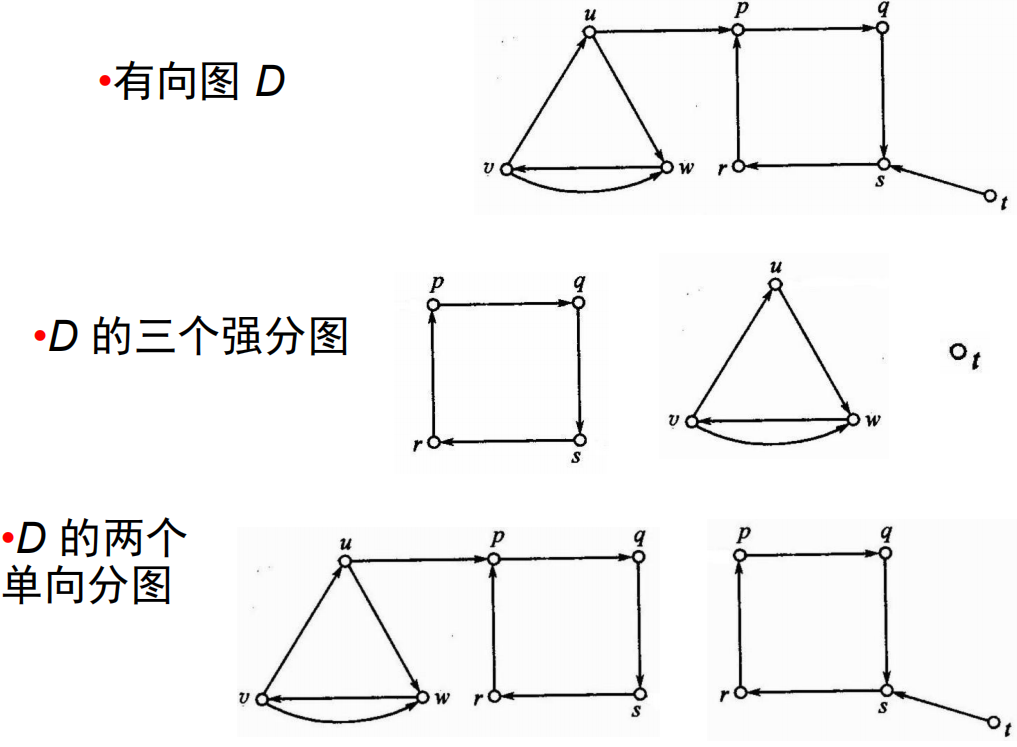
• 单向连通的：（任意两点至少一个方向可达）在有向图 中，如果任取一对顶点 和 ，或者 可以到达 ，或者 可以到达 ，则称 为单向连通的。

• 弱连通的：（任意两点互相连接）在有向图 中，如果任取一对顶点 和 ， 连接到 ，则称 为弱连通的。
  每个强连通/单向连通图都是弱连通的。

• 不连通的：（不弱连通）若有向图 不是弱连通的，则称它为不连通的。

• k度连通的：称不连通的有向图为0度连通的；称弱连通的但不是单向连通的有向图为1度连通的；称单向连通的但不是强连通的有向图为2度连通的；称强连通的有向图为3度连通的。

• 完备通路：称通过有向图中所有顶点的通路为完备通路。

• 完备回路：称通过有向图中所有顶点的回路为完备回路。

• 完备半通路：称通过有向图中所有顶点的半通路为完备半通路。

• 有向图 是强连通的当且仅当 有一条完备回路。

• 有向图 是单向连通的当且仅当 有完备通路。

• 有向图 是弱连通的当且仅当 有完备半通路。

9.4.2 无向图 链 连通

• 链：在无向图中，每条边（除最后一条边之外）都与随后那条边相邻的边的序列 称为链。也将链 记为顶点的序列 ，其中对于每个 ，。
• 长度：称链 的长度 为 。
• 简单链：（各边不同）各边互不相同的链称为简单链。
• 基本链：（各点不同）各顶点互不相同（因而各边互不相同）的链称为基本链。
• 闭合链：（第一个点和最后一个点相同）若 ，则称 为闭合链。
• 圈：（第一个点和最后一个点相同且各边不同）顶点 各不相同，并且各边互不相同的闭合链 称为圈。
• 从u到v的距离
  • （对称性）
  • （三角不等式）
  • 当且仅当
    从到的最短通路的长度从可到达
• 连通：若顶点 和 之间存在链，则称 和 是连通的。
• 图的连通：若无向图 中任何两顶点都是连通的，则称 是连通的，否则说 是不连通的。
• 连通分支：无向图 的顶点之间的连通关系是等价关系。每个等价类是顶点集的一个非空子集。由等价类导出的子图称为 的连通分支，等价类的数目即连通分支的数目。
  图 是连通的当且仅当 只有一个连通分支。
• 割点：设 是连通无向图 的顶点，如果从 中去掉 和与它关联的边得到的无向图 是不连通的，则称 为 的割点。
• 割边/桥：设 是连通无向图 的边，如果从 中去掉 得到的无向图 是不连通的，则称 为 的割边或桥。

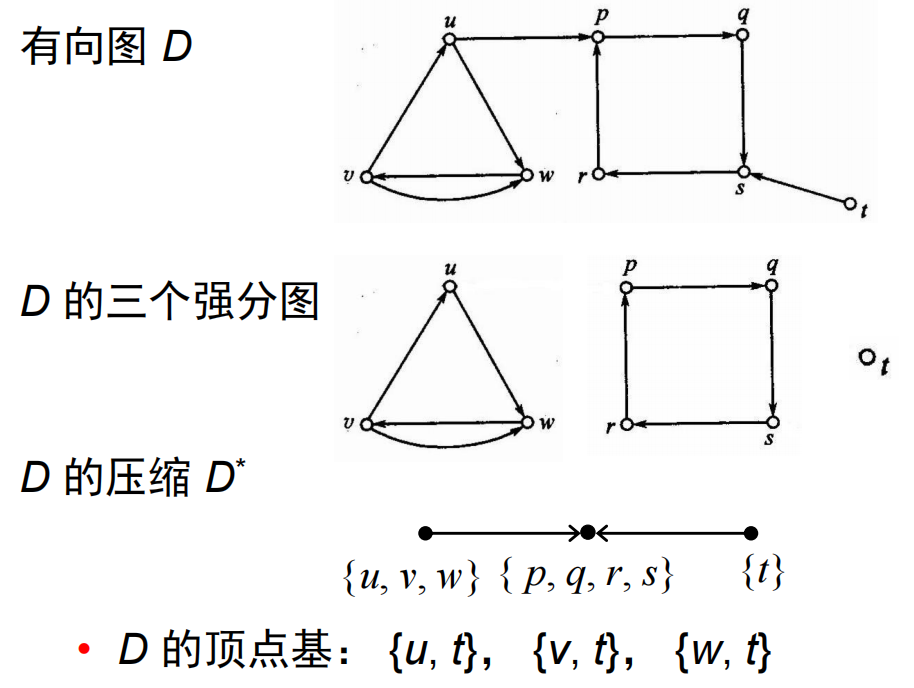
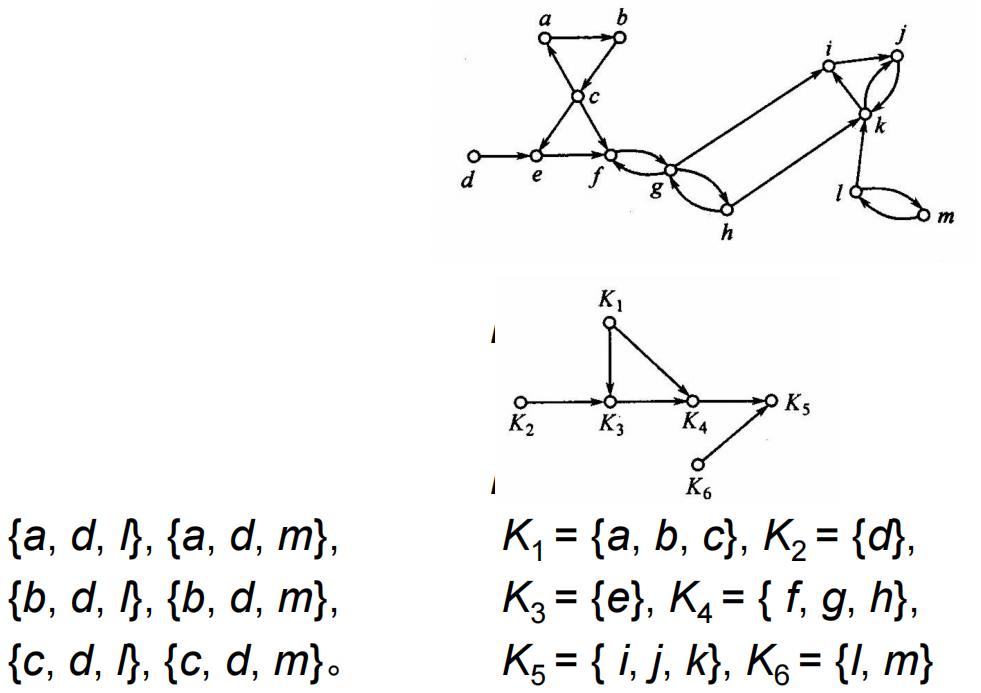
9.5 顶点基和强分图

9.5.1 顶点基

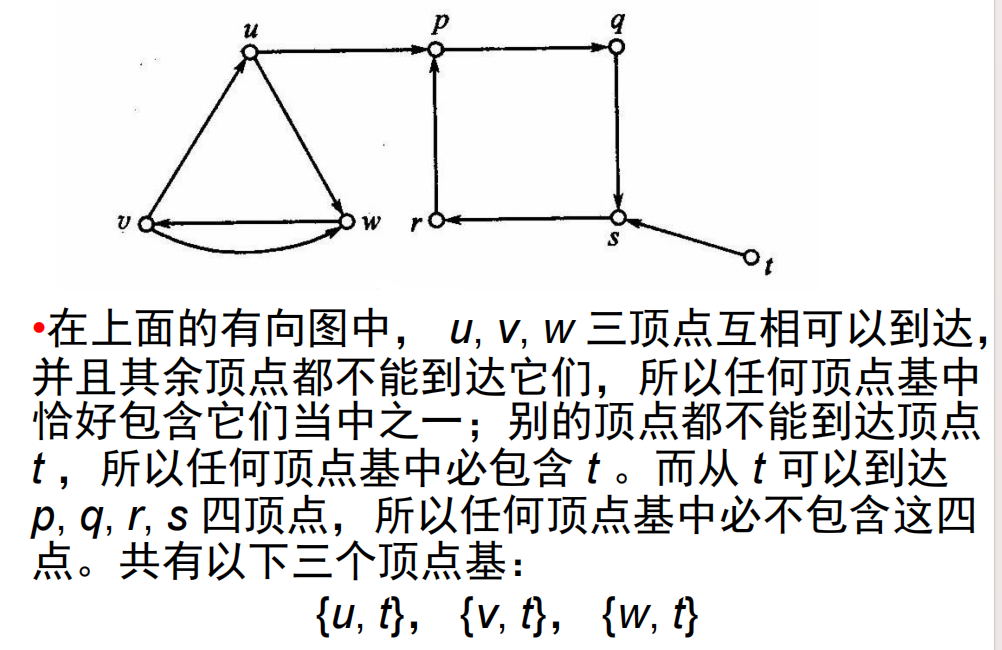
• 设有向图 ， ， 。若从 中某个顶点可以到达 ，则称从 可以到达 。
• 顶点基：（可达所有点且极小）设有向图 ，。若从 可以到达 中每个顶点（相当于 可以到达 中的每个顶点，因为 中的点可以到达自身），并且 的每个真子集都不能到达 中每个顶点），则称 为 的顶点基。
  

9.5.2 强分图

• 强分图：（极大的强连通子图）设 是有向图。若 是 的强（单向、弱）连通子图，并且对于 的任意强（单向、弱）连通子图 ，若 ，则 ；那么就称 为 的强（单向、弱）连通分图，或强（单向、弱）分图。
• 定理9.8：在有向图 中，每个顶点在唯一的强分图中，每条弧至多在一个强分图中。
  • 即在一个有向图中没有不在强分图中的顶点；任意两个强分图都没有公共顶点
  • 若弧 在两个强分图中，则它的端点在两个强分图中。
    

9.5.3 压缩

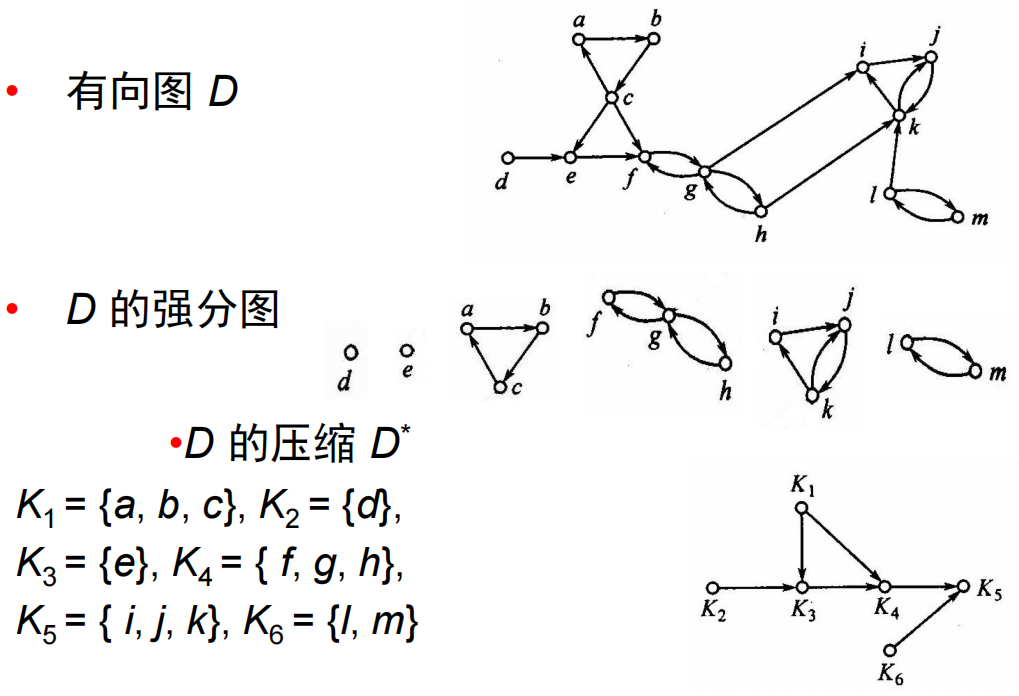
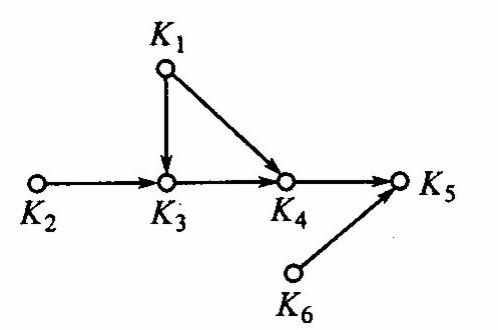
• 压缩：（强分图之间的弧组成的图）设有向图 的强分图的顶点集为 ，有向图 定义为 ，
  
• 定理9.9：有向图 的压缩 是无回路图。
• 定理9.10：无回路有向图（如压缩） 有唯一的顶点基，它由所有引入次数为 0 的顶点组成。
  
• 定理9.11：（压缩的顶点基中每个元素取出一个顶点可以构成原图的顶点基）设 是有向图 的压缩， 是 的唯一顶点基，则从 的每个元素中取出一个顶点构成的集合 是 的顶点基，并且 的每个顶点基都可以这样得到。
• 定理9.12：有向图 的每个顶点基都包含同样数目的顶点。
  
  

9.6 总结

• 根据图的结构特点，定义出多种图的名称
  无向图、有向图、带权图、邻接、关联、相邻、自环、平行弧/边、多重图、简单图、次数、n阶图、零图、平凡图、完全图
• 对于图和图之间的比较，定义出多种图的名称
  补图、正则图、同构图、子图(生成子图和导出子图)、图的并集
• 考察不相邻节点之间的关系，定义出新的概念
  通路及回路、简单通路及回路、基本通路及回路、可达、半通路、连接到、强(单向/弱)连通、完备通路(回路/半通路)、链、简单链、基本链、闭合链、圈、连通分支
• 根据连通图中特殊点和边的特点，定义出新的概念
  割点、割边/桥、顶点基、强分图(单向分图/弱分图)、压缩