13.1 欧拉图
无向图中的欧拉图
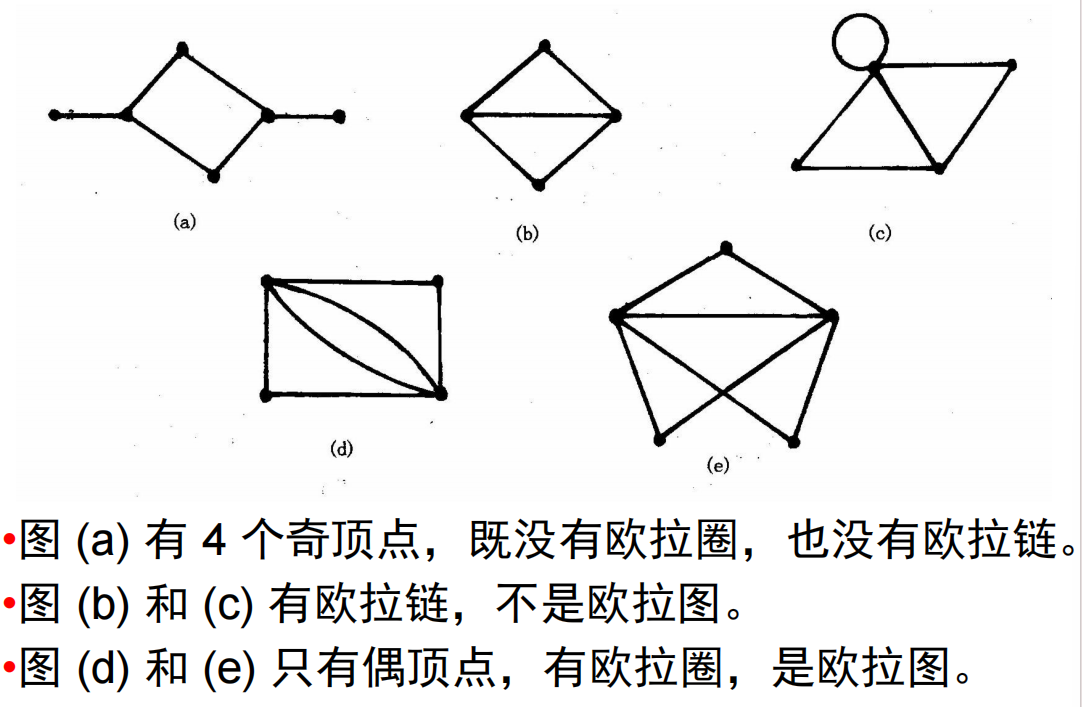
- 欧拉圈、欧拉图:称穿过无向图中每条边的简单闭合链为欧拉圈。有欧拉圈的图称为欧拉图。
- 若无向图
- 定理13.1:连通无向图
- 欧拉链:称穿过无向图
- 定理13.2:在连通无向图
一笔画问题
从无向图的一个顶点出发,笔不离纸,不重复地画出该图的所有边。
- 若连通无向图只有偶顶点,则从任意顶点出发,可沿欧拉圈不重复地一笔画出所有边,并回到出发点。
- 若连通无向图只有两个奇顶点,则从一个奇顶点出发,可沿欧拉链不重复地一笔画出所有边,并到达另一个奇顶点。
- 若连通无向图有多于两个奇顶点,则不能不重复地画出该图的所有边。
有向图中的欧拉图
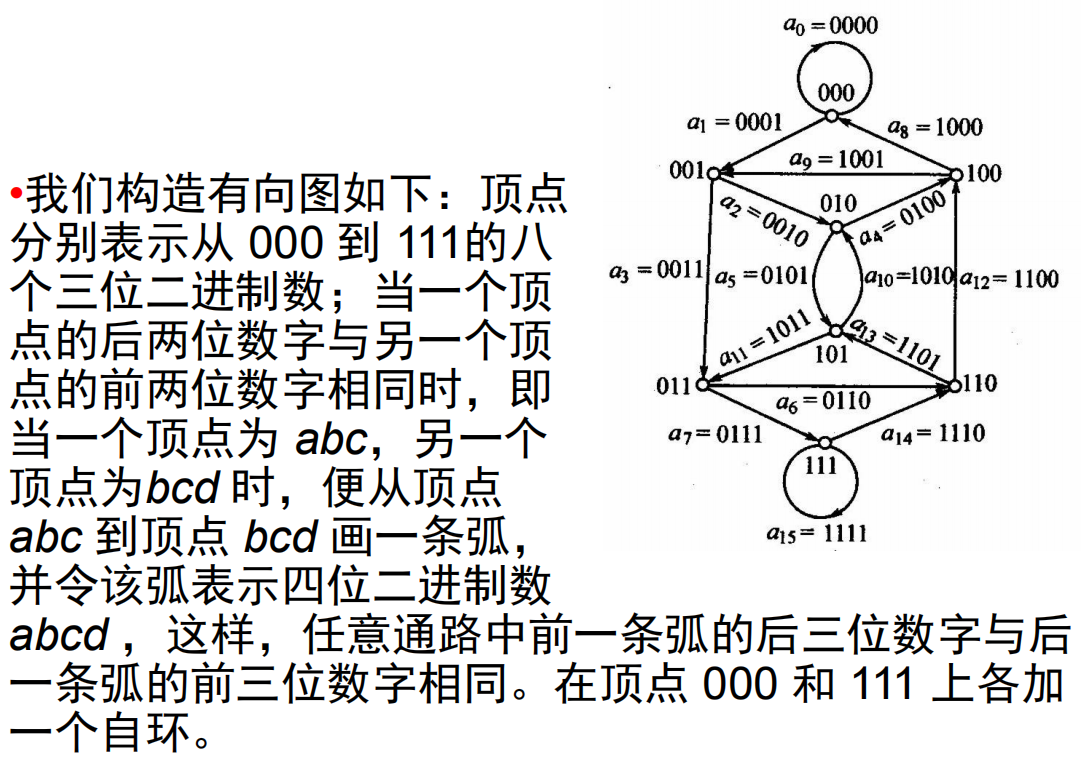
- 欧拉回路、欧拉图:称穿过有向图中每条弧的简单回路为欧拉回路。有欧拉回路的有向图称为欧拉图。
- 欧拉通路:称穿过有向图中每条弧且非闭合的简单通路为欧拉通路。
- 强连通有向图
- 单向连通有向图
13.2 哈密顿图
-
哈密顿圈、哈密顿回路、哈密顿图
- 称穿过无向图
- 称穿过有向图
- 有哈密顿圈或哈密顿回路的图称为哈密顿图。
- 称穿过无向图
-
哈密顿链:称穿过无向图
-
哈密顿通路:称穿过有向图
-
从哈密顿回路中去掉一条弧就成为哈密顿通路,从哈密顿圈中去掉一条边就成为哈密顿链。哈密顿回路是完备回路,哈密顿通路是完备通路,所以有向哈密顿图是强连通的,存在哈密顿通路的有向图是单向连通的。存在哈密顿链的无向图是连通的。
-
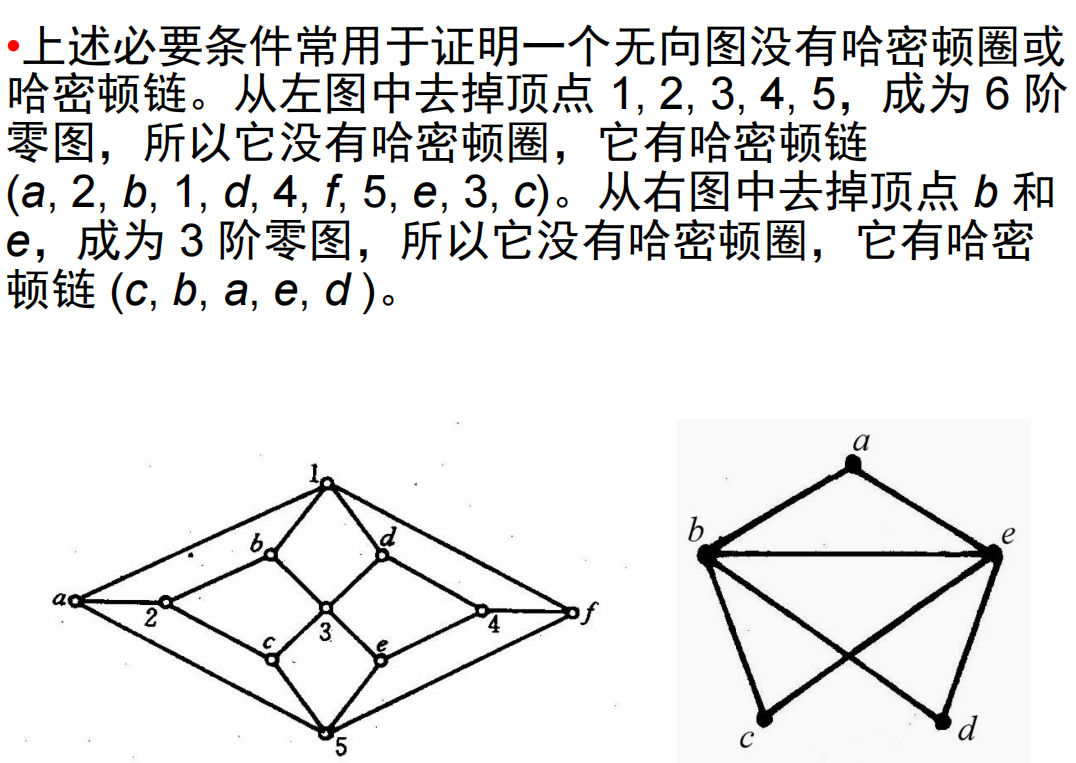
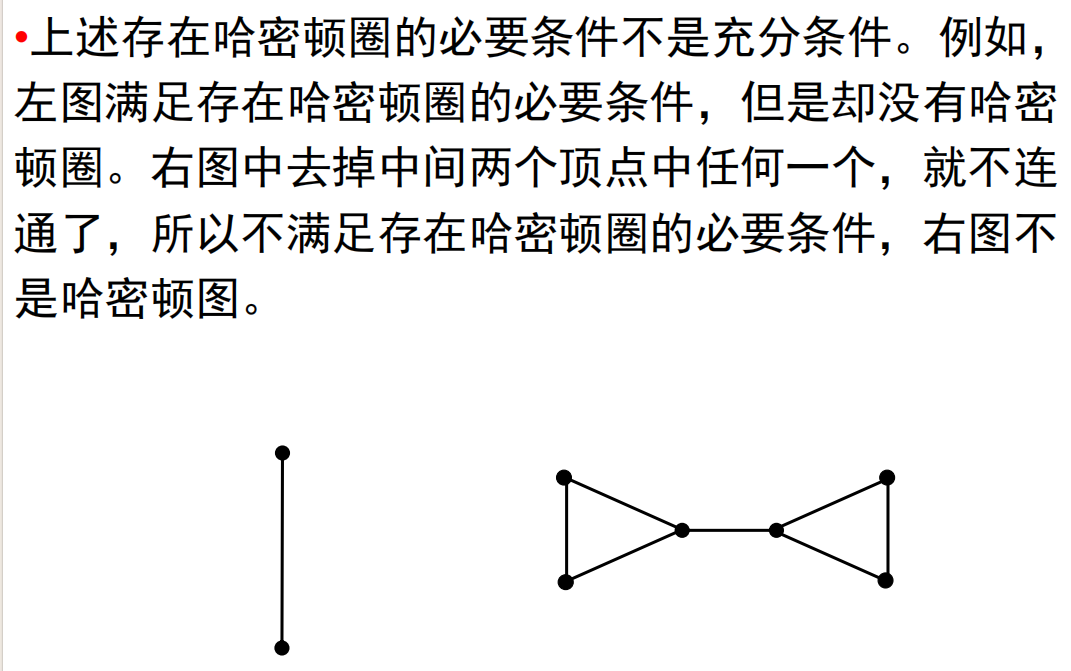
哈密顿图的必要条件(只能判断不是哈密顿图):若无向图
=
-
哈密顿链的必要条件(只能判断不是哈密顿链):若无向图
=
-
定理13.3(哈密顿链的充分条件):若
-
哈密顿图的充分条件:设
-
定理13.4:在有向完全图中必存在哈密顿通路。
-
凡是强连通的有向完全图一定有哈密顿回路。