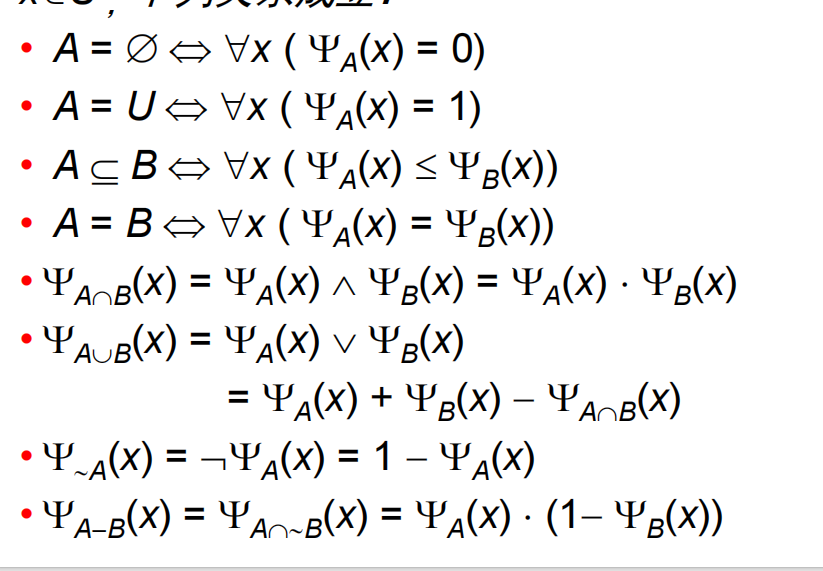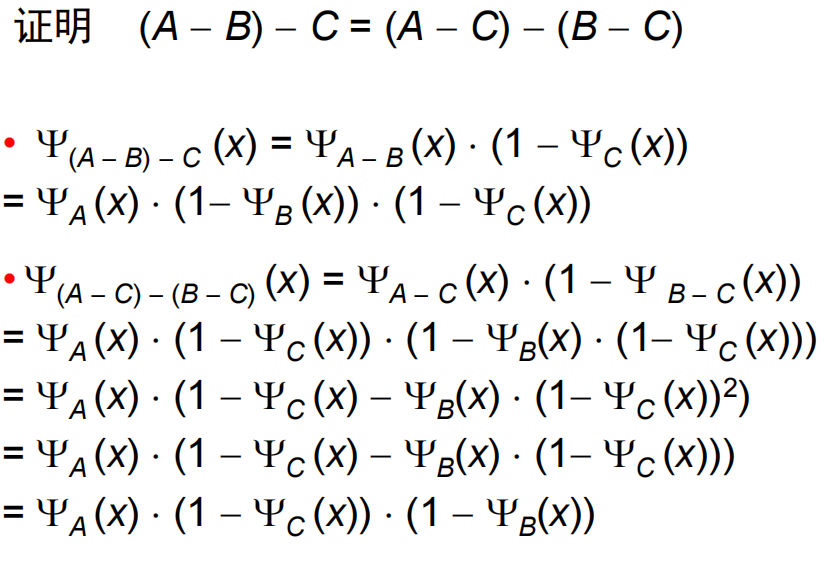7.1 基本概念

函数：如果关系满足单值性（若且，则），那么就称为函数。
从X到Y的函数：设是从集合到的关系。若对每个存在唯一使得，则称为从X到Y的函数，记为。（这里从到的函数指的是单值全函数）
从X到Y的函数的判定标准

，即处处有定义
是函数，即单值性
象、象源对于函数，若，则称为自变量，为函数在处的值。也称为在作用下的象，而称为的一个象源。常用表示。
常用函数
- 恒等函数：
- 后继函数：
- 地板函数：
- 天花板函数：
限制与开拓：设函数，又，则是从到的函数，称为 受限制于 ，记为，又称为的开拓。
- 只是去掉那些以不在中的元素为第一元的有序偶，将定义域改为，并不改变函数值：对于每个。
象：设函数，。称集合为在下的象，记为。
- 显然，整个定义域的象成为函数的象，即的值域，也即：。
- 由函数派生出函数。
从X到Y的偏函数：设是从集合到的关系。若对每个存在唯一使得，则称为从到的偏函数，又称为部分函数
- 是从集合到的函数当且仅当
  - 为从到的偏函数
Y上X：用表示所有从到的函数组成的集合，即，读作“ 上 ”
- 若和都是有穷集合，则
- 设，，则可有种选择，所以
- 对于任意集合，
- 若是非空集合，则
- 设是全体命题变元组成的集合，则是全体真值赋值组成的集合。
函数和一般关系的差别（对于有限集合）
- 集合个数存在差别：从到的不同关系共有个，从到的不同函数有个
- 集合的基数（集合内元素的个数）存在差别：每一个关系的基数可以从一直到，每一个函数的基数都为个
- 集合元素的第一元存在差别：关系的第一元可以相同，函数的第一元一定互不相同。

7.2 函数的复合

若且，则函数的复合是一个从到的函数，即，且对所有的，。
和是恒等函数，函数，则。
设由函数，及，则函数的复合具有可结合性。即。
f的n次复合；设，定义如下：
多元函数：若函数的定义域是个集合的笛卡尔乘积，则称为元函数，并将记为
- 若，则称为上的二元运算，常采用中缀记法，将记为，如实数加法。

7.3 特殊性质的函数

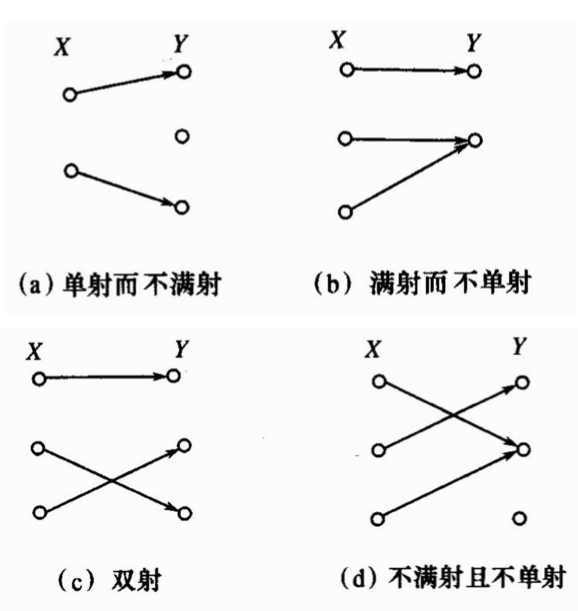
设函数
- 满射：若对于每个都存在使得，即，则称为满射的。
- 单射：若对于任意，只要，就有，即只要，就有，则称为单射的。
- 双射/一一对应：若即是单射又是满射的，则称是双射的，或一一对应。
- 具有上述特性的函数分别称满射函数，单射函数，双射函数。
对于实函数，即，可以通过的图像判断是不是满射、单射、双射
- 是满射当且仅当，每条与横轴平行的直线与的图像至少有一个交点。
- 是单射当且仅当，每条与横轴平行的直线与的图像至多有一个交点。
- 是双射当且仅当，每条与横轴平行的直线与的图像恰好有一个交点。
设是从到的函数，是从到的函数
- 若和都是满射，则是满射。
- 若和都是单射，则是单射。
- 若和都是双射，则是双射。
常值函数：设函数。如果对于所有的，存在某一个，使得，即，则称为常值函数。
关于逆函数
- 若单射，则单值。
- 若满射，则处处有定义。
- 定理7.4：若双射，则也是双射函数。若不双射，则不是函数
反函数：设是双射函数，称的逆关系为的反函数。
可逆：设，如果存在使得且，则称为可逆的。
定理7.5：若是双射，则且
定理7.6：设双射及双射，当且仅当且。
定理7.7：若双射及双射，则也是双射，并且
补充：双射集合构成群
设是所有从 X 到 X 的双射函数组成的集合
- 封闭性：对于任意，和都。（此性质也称为复合运算的闭包性）
- 结合律：对于任意，
- 有单位元：，对于任意，
- 有逆元：对于任意，存在反函数，
  是群

7.4 集合的特征函数

特征函数 ：设是全集的子集，的特征函数定义为 $若若$
设是全集的任意两个子集，则对于所有，下列关系成立