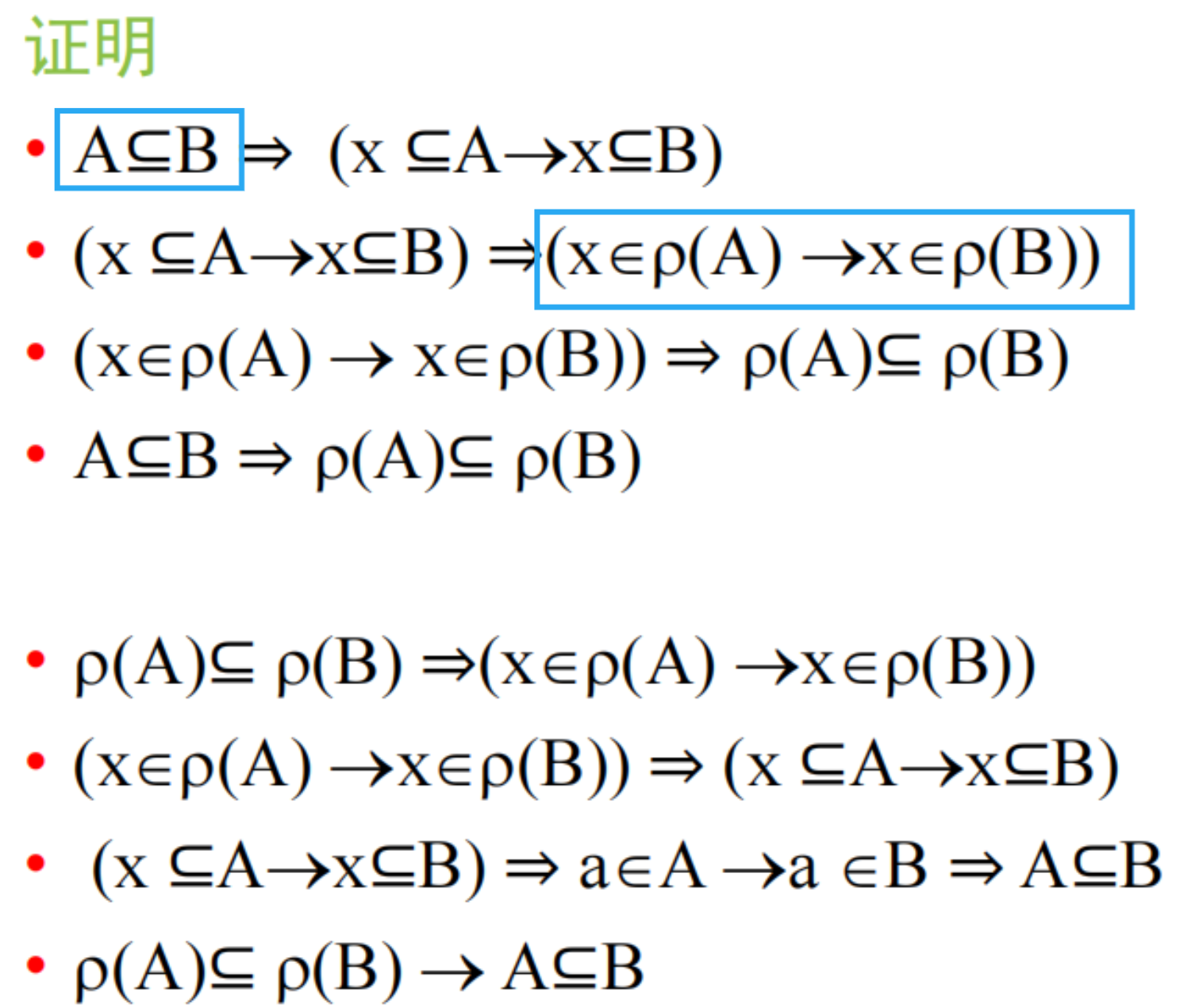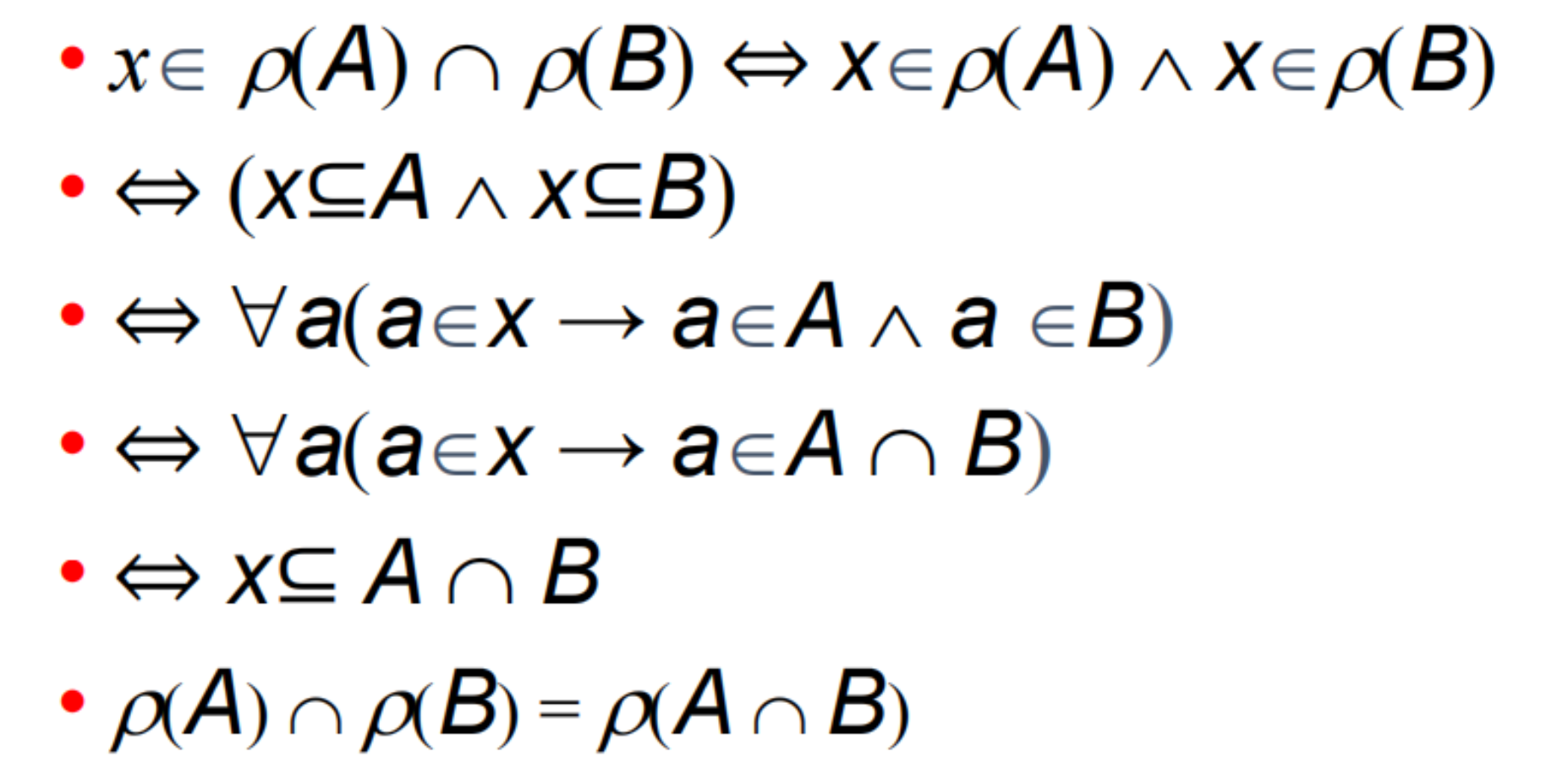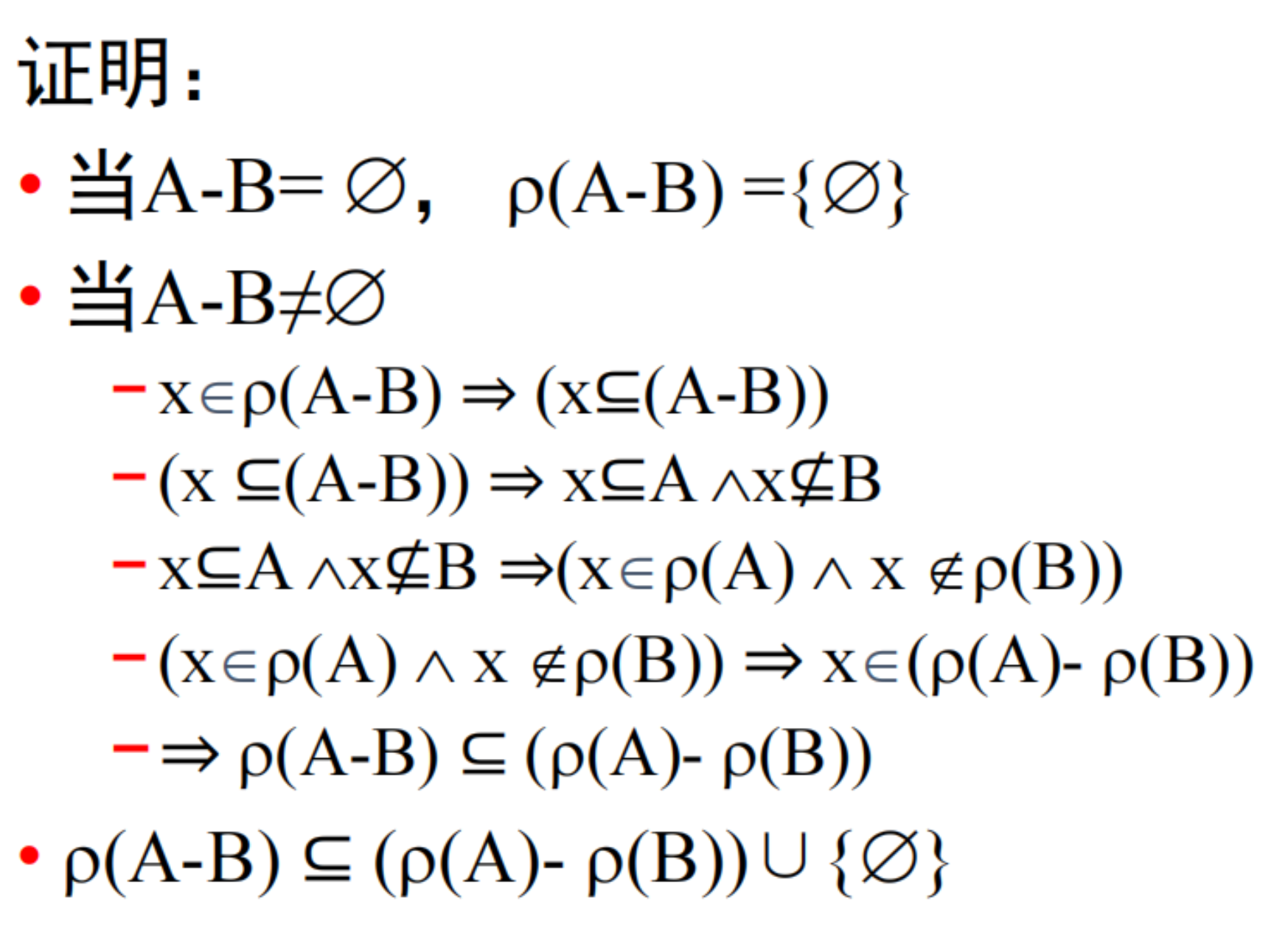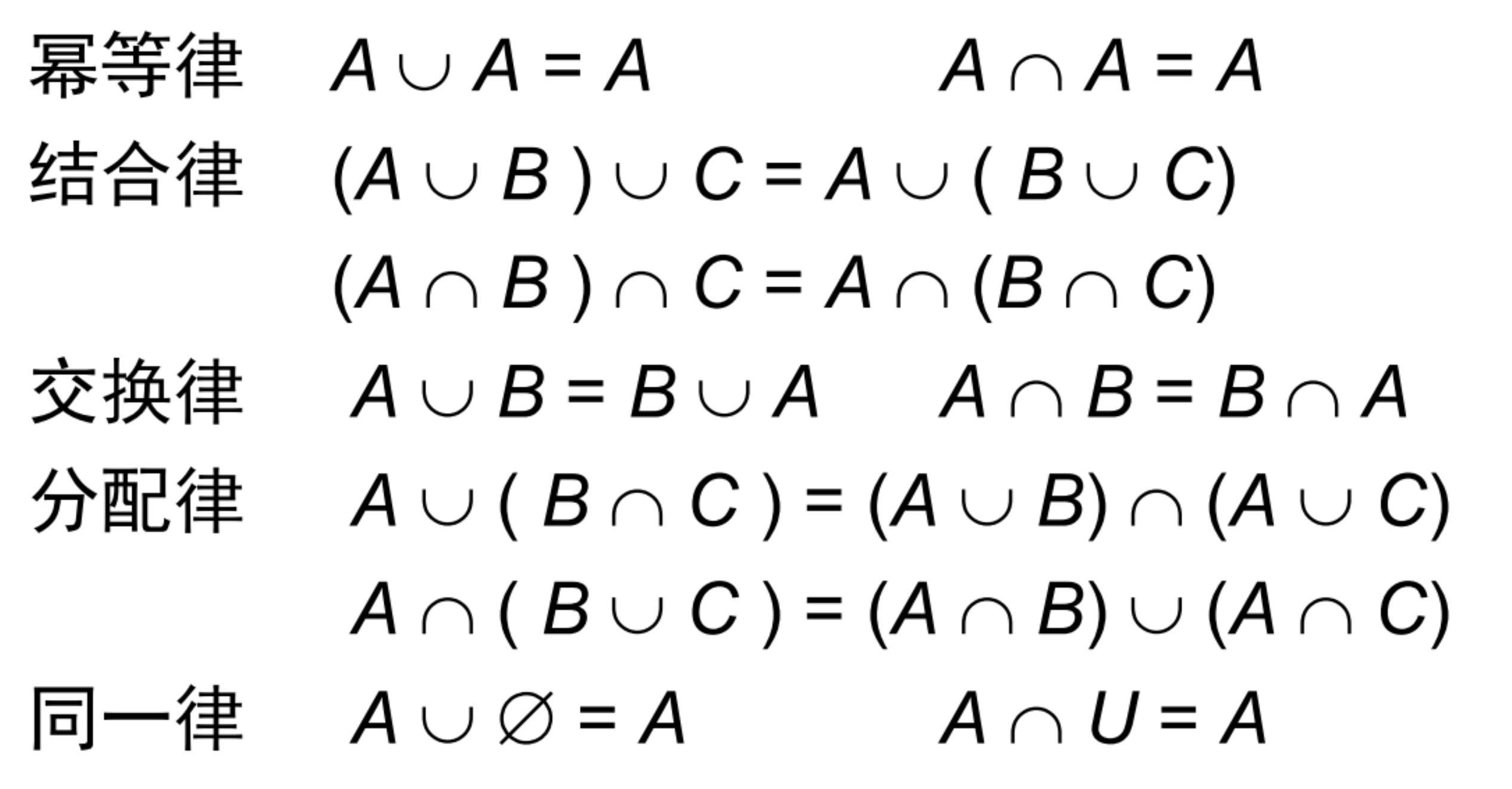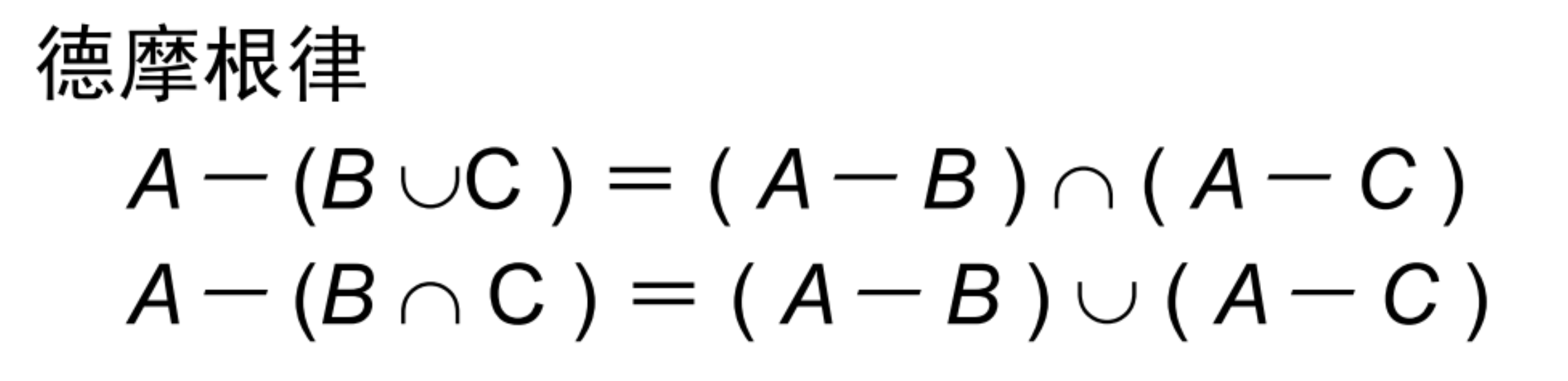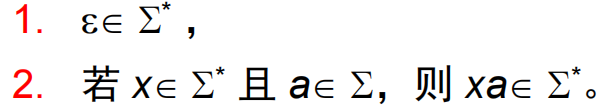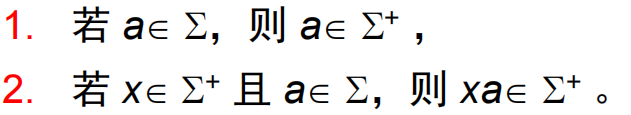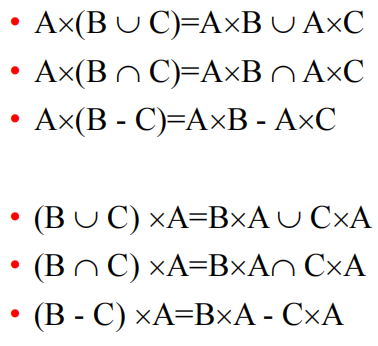5.1 集合与元素
- 集合、元素:通常用大写英文字母
- 集合中元素无次序
- 集合中元素不考虑重复出现
- 如果对象 a 在集合 A 中,则称 a 是A 的元素,或者 a 属于 A,记为
- 表示方法:枚举法、抽象法
- 常用集合:自然数集
- 抽象原则:
- 任给一个性质
- 即假设
- 任给一个性质
5.2 集合间的相等和包含关系
- 外延公理:设
- 子集:若集合
- 真子集:若
- 定理5.1:设 A 和 B 是两个集合,则
- 推论:对于任意集合
- 定理5.2:设 A , B, C 是集合,若
- 全集:如果所讨论的集合都是集合
- 空集:不含任何元素的集合称为空集,记为
= , 为 实 数 - 定理5.3:空集
- 定理5.4:空集
- 定理5.3:空集
- 单元集、n元集、有穷集、无穷集
- 单元集:含有一个元素的集合
- n元集:含有
- 有穷集:由有限个元素构成的集合
- 无穷集:由无限个元素构成的集合
5.3 幂集
- 幂集:由集合
- 空集的幂集仅含有元素
- 单元集A的幂集为
- 对于任意集合
,
- 空集的幂集仅含有元素
- 基数和幂集的基数
- 有穷集
- 定理5.5:
- 有穷集
- 幂集的性质
5.4 集合的运算
1 简单计算
- 交集、并集、差集
- 聚合/集合族:如果集合
- 若集合
- 设
- 补集:
- 对称差集:
2 集合恒等式
- 集合恒等式
- 集合代数满足对偶定理:在不含
- 将不含
- 集合代数满足对偶定理:在不含
集合恒等式 A=B的证明方法
-
法1:使用集合相等的定义,证明:对于任意
-
法2:证明
-
法3:利用已知集合恒等式进行等式推演
-
例
-
定理5.9:设
-
-
例
-
3 广义并、广义交
-
广义并、广义交
- 广义并:
若 - 广义交:若
若
有时将集合族的元素表示为带角标的集合,如
也将 - 广义并:
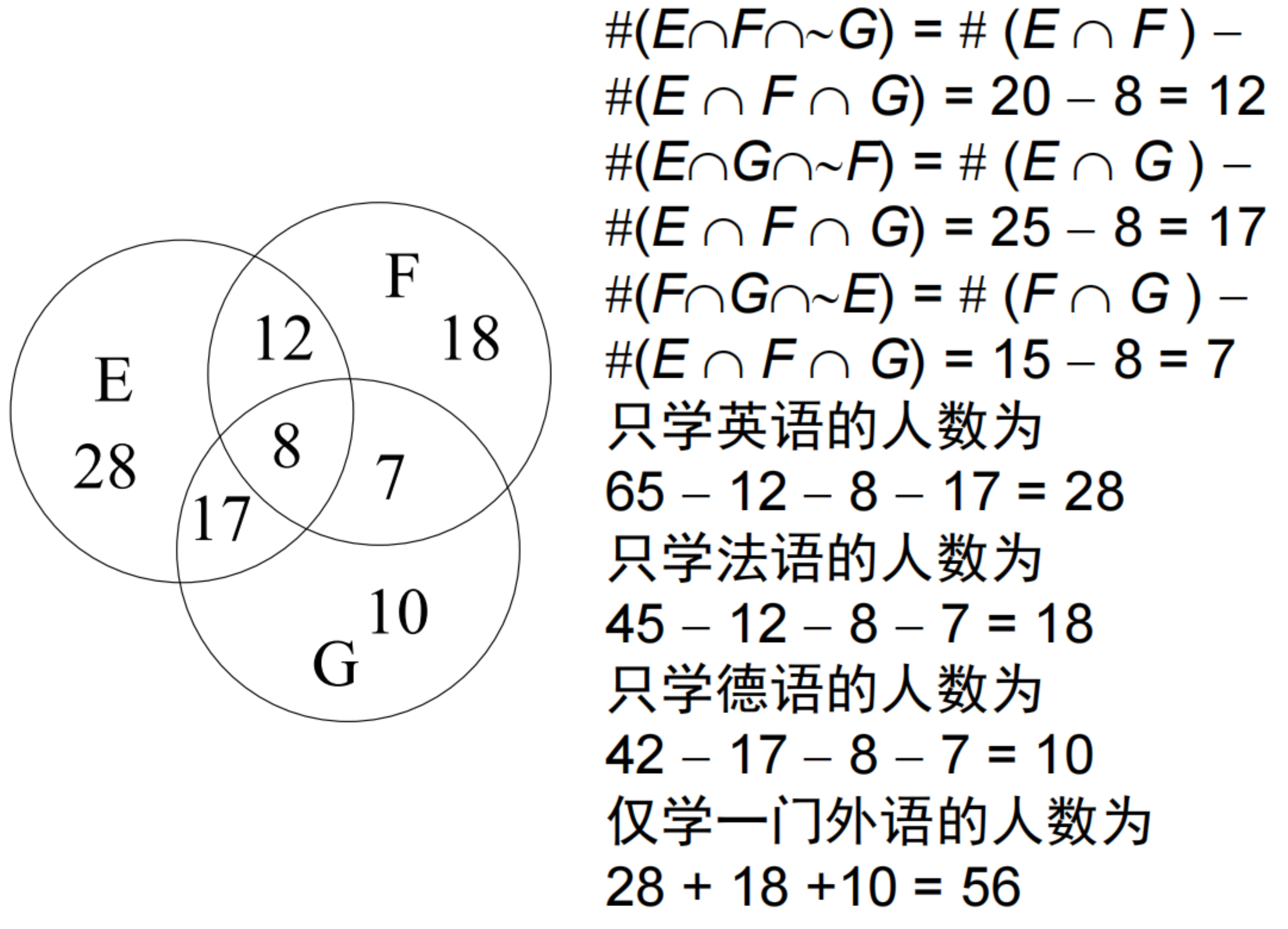
5.5 有穷集的计数原理
- 设
- 包含排斥原理:若
- 推论:若
- 推广:设
- 推论:若
5.6 集合的归纳定义法
集合归纳定义的三个组成部分
- 基础语句:直接规定某些对象是该集合的元素。这保证了所定义的集合是非空的,同时也规定了构造集合的原子元素。
- 归纳语句:规定由已知元素得到新元素的办法。
- 极限语句:限定集合的范围,规定了哪些对象不是该集合的元素,保证了定义的集合是唯一的
极限语句常省略不写
非负偶数集 E 可归纳定义如下:
基础语句 0\in E,
归纳语句 若 n \in E, 则 n + 2 \in E 。
字母表
-
字母表(符号集):符号的有穷非空集合称为字母表,通常用
-
-
长度:
-
空串:长度为 0 的字称为空串,记为
-
连接:字母表
连接运算满足结合律,即
连接运算不满足交换律,如设
对于任意字x, -
所有
-
所有
显然, -
设
-
称
-
乘积运算满足结合律
乘积运算不满足交换律 -
定义5.20 设
-
定理5.13
-
定理5.14:设
- 若
-
设A是
= 是 自 然 数 = = - 集合
= =
-
定理5.15
5.7 有序偶和笛卡儿乘积
- 设 n > 2,n 重序偶定义为
- 集合 A 和 B 的笛卡儿乘积
- 对于任意有穷集合 A 和 B ,
- 笛卡尔积的性质