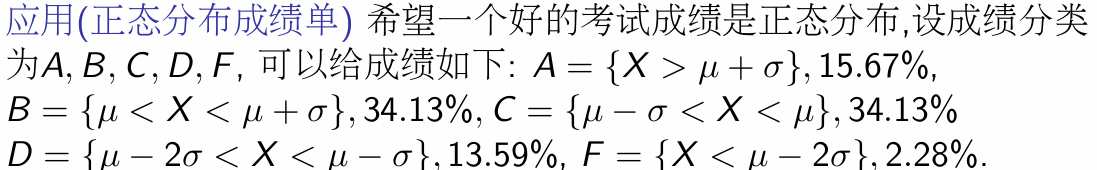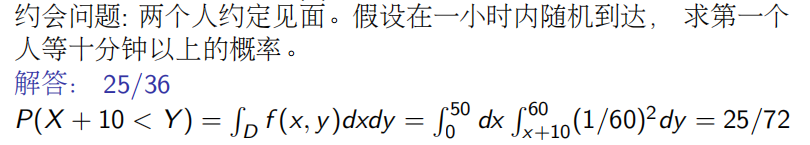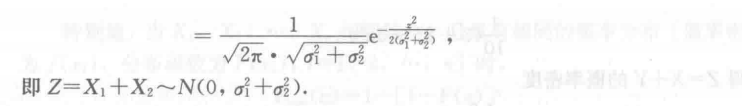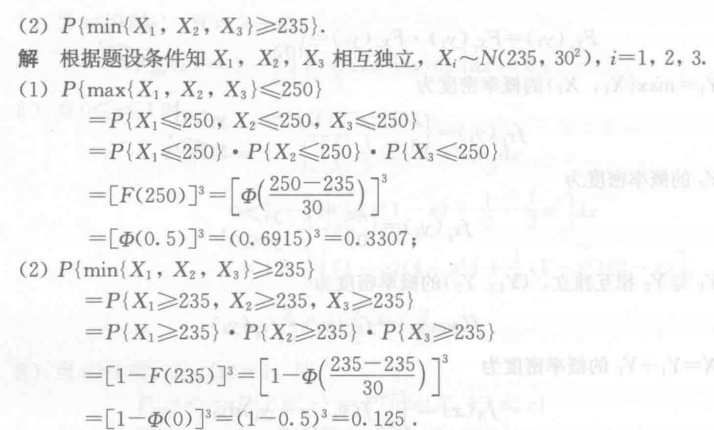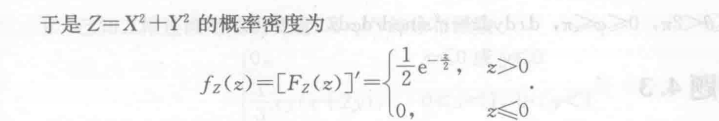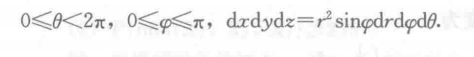1 一维
1.1 离散随机变量&离散分布
- 概率分布函数:
特别地,如果 - 概率分布函数的性质
- 概率分布函数的充要条件
单 调 非 减 , ,
- 推论
- 概率分布函数的充要条件
常见离散分布
离散随机变量:随机变量取值为有限或可数个时,称为离散随机变量。记其值为
1 两点分布
- 概率模型:一次试验是否成功
2 二项分布
- 随机变量
, , - 概率模型:N次独立试验中的成功次数。
- 应用:投票权大小(委员会组成);比赛规则(三局两胜,五局三胜)
3 几何分布(Geom(p))
- 随机变量
- 概率模型:重复试验直到首次成功时的试验次数。
- 应用:离散等待时间和无记忆性
4 超几何分布
- 随机变量
- 概率模型:从
- 数学近似:较大N,M时,可以用二项分布
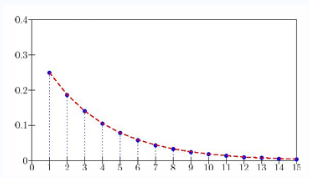
5 泊松分布
- 随机变量
, , - 概率模型:大量试验中的小概率事件发生次数。每年发生战争的次数,某一小时进入某邮局的顾客数,寿命超过100岁的人数
- 数学近似:二项分布B(n,p),当n大p小,np合适大小时,可用
例:设二项分布B(100,0.01),计算
用Poisson分布
1.2 连续随机变量&连续分布
- 连续随机变量:
tips:随机变量的取值可能既包含离散值,也包含区间,可以称为混合型随机变量 - 概率密度函数的性质
- 密度函数的充要条件:
- 分布函数F(x)与密度函数f(x)的关系
- 密度函数的充要条件:
常见连续分布
1 均匀分布
如果连续随机变量X的密度函数满足
记为
- 概率分布函数:
- 概率模型:等可能事件的推广
2 指数分布
如果连续随机变量X的密度函数满足
记为
- 概率分布函数:
几何分布与指数分布: - 模型:小概率事件之间的间隔时间(等待时间)
下一次类似汶川地震发生的时间;人或机器的寿命;排队时间; - 指数分布的无后效性:(在指数分布过程中,未来的事件发生概率只与当前时刻有关,与之前的事件无关;对于任意时间点t,事件在未来时间段Δt内发生的概率只依赖于Δt的长度,而与t无关)
排队等待概率:设有两个窗口,两个人正在办理,每个人的办理时间服从指数分布 - 失效函数(失效率、死亡率):定义
解释:寿命到达t时刻后在dt内失效的概率。
指数分布的失效函数为常数
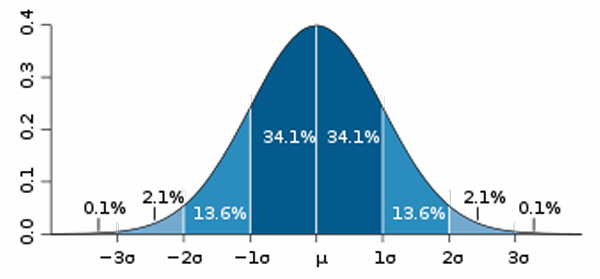
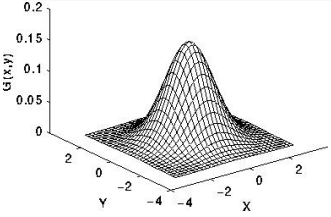
3 正态分布(高斯分布,Bell曲线Normal)
如果连续随机变量X的密度函数满足
特别称
- 概率分布函数:无初等表达式,需要查表。
定义:任意 - 模型:大量物理或生物数据的特征指标;
高斯分布:研究测量误差的分布;IQ分数,成绩; - 本质上是二项分布的逼近:n充分大当可用正态分布近似计算。
3.1 标准正态分布
-
密度函数
-
分布函数
-
定理:
-
概率密度函数性质:关于0点对称,0点最大,两边单调。
-
概率分布函数性质:
-
标准正态分布表:一般记
标准正态分布的常见分位数:
3.2 正态分布及分位数
- 正态分布的线性变换:如果
- 正态分布的取值分布:短尾分布(尾部即与分布的两段衰减的很快)
应用:
1.3 复合离散随机变量&分布
设离散型随机变量
-
若对于
-
若对于
1.4 复合连续随机变量&分布
-
连续型随机变量
其 它 其中 (c,d) 为 y=g(x) 的值域。
-
若函数 y=g(x) 不是严格单调的,但是在不相重叠的区间
, 其中,
-
正态分布
- 正态分布的线性变换:
设 则 服 从 。
- 折叠正态分布:
设 则 服 从 。 - 正态分布的平方
设 则 服 从 分 布 , 。
- 正态分布的线性变换:
2 二维
2.1 联合分布函数
- 随机向量的定义
- 随机向量:随机向量
- 随机向量:随机向量
- 联合分布函数 (Jointed-CDF)
- 联合分布函数:
- 分布函数的充分必要条件:
对 或 单 调 非 减 任 意 有
- 分类:二维离散随机向量,二维连续随机向量,混合型随机向量
- 分布函数的充分必要条件:
- 联合分布函数:
2.1.1 二维离散分布
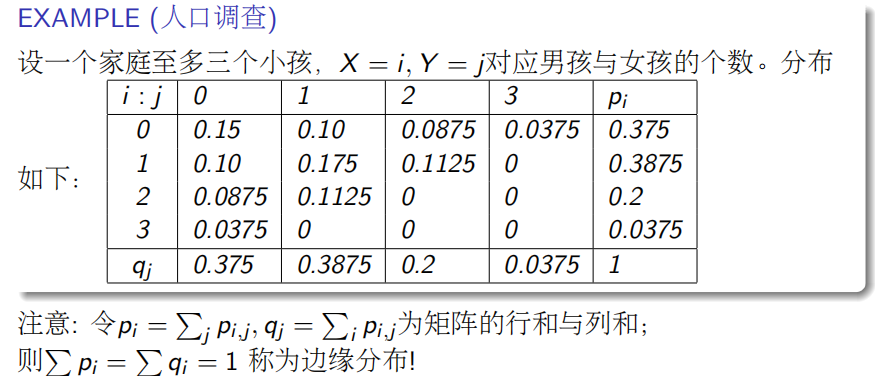
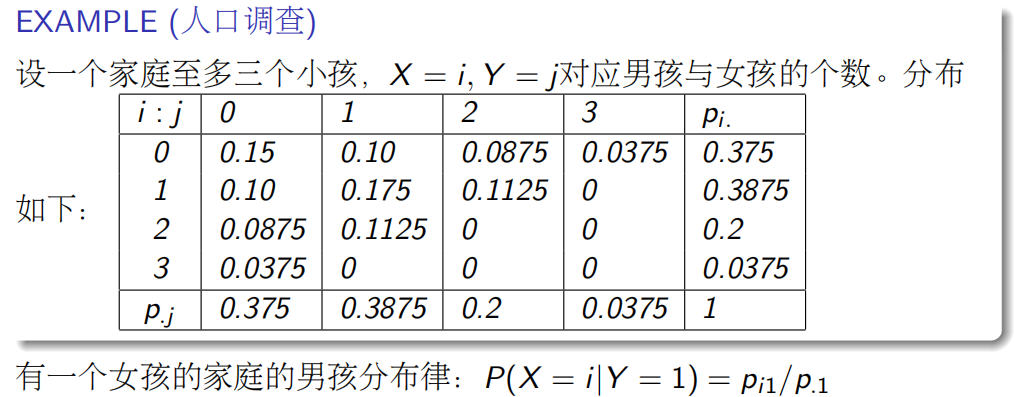
- 二维离散分布(矩阵):
记- 例
2.1.2 二维连续分布
- 二维连续随机向量:
- 分布函数
- 定理:连续可微的联合分布函数有联合密度函数,所以是连续随机向量。即
- 分布函数
- 二维均匀分布:
- 二维正态分布:给定
- 参数
- 参数
2.2 边缘分布
- 边缘分布:
- 边缘分布函数:
- 二维离散情形:可定义边缘分布列(即矩阵的行和或列和)
- 二维连续情形:存在对应的边缘密度函数
- 联合分布决定边缘分布,反之不能
- 边缘分布函数:
- 例
2.3 条件分布
- 离散情形
- 连续情形:
- 乘法公式
2.4 连续二维分布
1 均匀分布
圆盘上的均匀分布:求
2 正态分布
设
边缘分布
条件分布
3 独立性和高维复合随机变量
3.1 独立性
- 定义
- 随机变量
相 互 独 立
- 随机变量
- 性质
- 常数与任意随机变量独立;
- 二维正态分布的坐标随机变量相互独立的充要条件是
3.2 二维随机向量的复合分布
- 随机向量的函数
随机向量
二维离散型随机变量
设离散型随机变量
-
若对于
-
对于
二维连续型随机向量
一般方法:
连续情形1:
二维连续型随机变量
对任意实数
- 设
连续情形2:
- 二维随机变量
若 与 独 立 - n维相互独立的随机变量
连续情形3:
- 二维随机变量
若 独 立 - n维相互独立的随机变量
连续情形4:旋转不变的随机变量
- 极坐标变换
- 设
例
- 例1
- 例2
- 例3
- 例4
- 例5
- 例6
- 例7