01 概率模型

1 样本空间

  1. 样本空间：试验的全部基本事件组成的集合，称为试验的样本空间，记为或。
    1. 试验的基本事件：是样本空间的元素(样本点)。
    2. 随机事件是样本空间的子集。
    3. 不可能事件表示空集，必然事件表示全集（样本空间）。

2 概率律

  1. 概率律

    例：

    古典概率模型：，#表示数目（即时间A的数量除以样本空间事件总数）

  2. 可数样本空间：几何分布律

    1. 古典模型：集合有n个元素，每个元素课看成一个子集，成为基本事件（样本点）
    2. 可数模型（离散模型）：集合有可数个元素，每个元素可看成一个子集，可看成事件
      例：一个人打靶命中率为p，重复射击直到中靶，求在第n次打中的概率

      一般的，可数模型的概率对应一个收敛的几何级数

  3. 不可数样本空间：连续空间的概率密度函数

    1. 古典概率推广：几何概率 定义，其中表示其区域的面积或长度或体积
    2. 连续模型：集合有不可数个元素，每个元素可看成一个子集，但一点作为事件无意义
    约会问题

    image-20240918105800336.png

  4. 概率律的公理化

    1. 定义：
      设P(A)是定义在试验E的全体事件(包含∅和S)所组成的集合F（事件域）上的一个实值函数。若P(A)满足下列三个性质：
      (1) 非负性：对每一个 ,成立;
      (2) 规范性：；
      (3) 可数（列）可加性：如果是互不相容事件则
      称为的一个概率，记P(A)为事件A的概率。
    2. 基本属性
      1. ；有限可加性
      2. 单调性：，则

3 古典概率的计算

计数方法counting

  • （m次实验）：从n个元素中有放回的每次取一个；取出m个元素，排成一列；共有种可能；不同排列是等可能的
  • （m元排列）：从n个元素中无放回的每次取一个；取出m个元素，排成一列；共有种可能；不同排列是等可能的
  • （m元组合）：从n个元素中无放回的每次取一个；取出m个元素，放在一组；共有种可能；不同组合是等可能的
  • （k重分组）：将n个元素分成不同的k组，不考虑每组中的元素次序，第i个组恰有个元素的可能分组为种可能；不同分组是等可能的
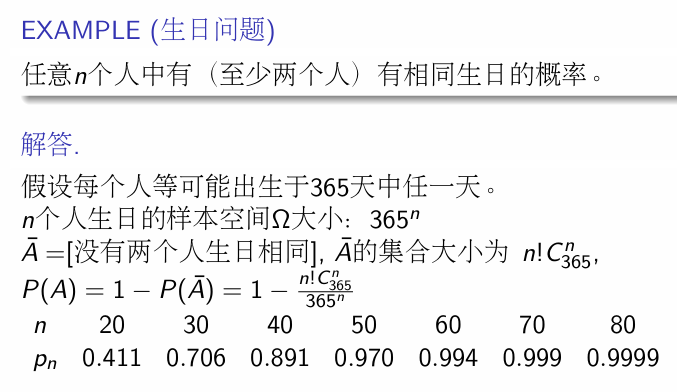
生日问题

image-20240906085710595.png

超几何分布

image-20240906085726678.png

4 集合运算

  1. 朴素集合论
    集合三要素
    • 补集：
    • 交集：”乘法“
    • 并集：”加法“
    • 其他：“减法”
    • 发生，则必然发生
    • 和是互不相容事件
  2. 集合论与概率事件
    • 集合一组研究对象 VS 样本空间
    • 每个对象称为元素，记为 VS 基本事件
    • 记子集满足一定条件特别任一有记 VS 事件
    • 某个基本事件发生，如果元素，则基本事件发生。
  3. 集合运算的主要公式
    1. 加减乘


    2. 运算规律
      交换律
      结合律
      分配率
    3. 德摩根律

    4. Venn分解


配对问题

image-20240906092125581.png

  1. 加法公式
    3. 容斥原理（约旦公式）：
      其中
再谈配对问题

image-20240911103304233.png

5 乘法公式，条件概率

  1. 定义：设A, B是时间，已知A发生，B发生的概率记为P(B|A)，其公式为，其中。
    用古典模型解释：
    记。是一个概率（满足概率公理）

  2. 条件概率满足概率公理化的三个条件：

    • 非负：
    • 归一化：
    • （可列）可加性：

  3. 条件概率下的条件概率：
    设有事件A，B，C，已知A发生，有条件概率P~A~，又已知B发生，有条件概率P~AB~，则

  4. 乘法公式
    ，可以推广到n个事件。

    扑克

    image-20240911105119382.png

    三门问题

    image-20240911105354276.png

6 全概率公式，贝叶斯公式及应用

  1. 全概率公式
    可以推广到n个互不相容事件（满足）

    风险评估

    image-20240911110114781.png

  2. 贝叶斯定理

  3. 贝叶斯公式（逆概率公式）
    ，可以推广到n个互不相容事件。

    赌牌游戏

    image-20240911111742142.png

    抽签原理

    image-20240911112135460.png

    假阳性之谜

    image-20240911114507519.png

7 系统与独立性

  1. 2个事件独立：如果A，B满足，称事件A，B互相独立
  • 如果A，B独立，则
  • 不相容事件不相互独立（）
  • 必然事件和不可能事件∅与任何事件相互独立
  • 如果，独立，则，相互独立，，相互独立，，相互独立
  1. n个事件独立：如果满足，任取其中个事件，有。称相互独立。
  2. 系统：系统有若干元件组成，系统的可靠性由元件的可靠性和系统的结构（网络）共同决定
  • 基本假定：所有元件都是相互独立的。
  • 连接方式：并联或串联。
    设每个元件正常工作的概率为P(A~i~)
    串联：
    并联：
Built with MDFriday ❤️